You should know about 01 backpack!
This week we officially began to explain the backpack problem!
The classic material of knapsack problem is, of course: knapsack nine lectures. In the official account of the public code, the backstage reply: knapsack nine, you can get pdf in the knapsack nine.
But to tell the truth, backpack nine is really not friendly to Xiaobai. It seems a little laborious, and it's all pseudo code, which is also difficult to understand.
For the interview, it's enough to master 01 backpack and complete backpack. You can have another multiple backpack at most.
If these backpacks cannot be distinguished, I draw a picture here, as follows:
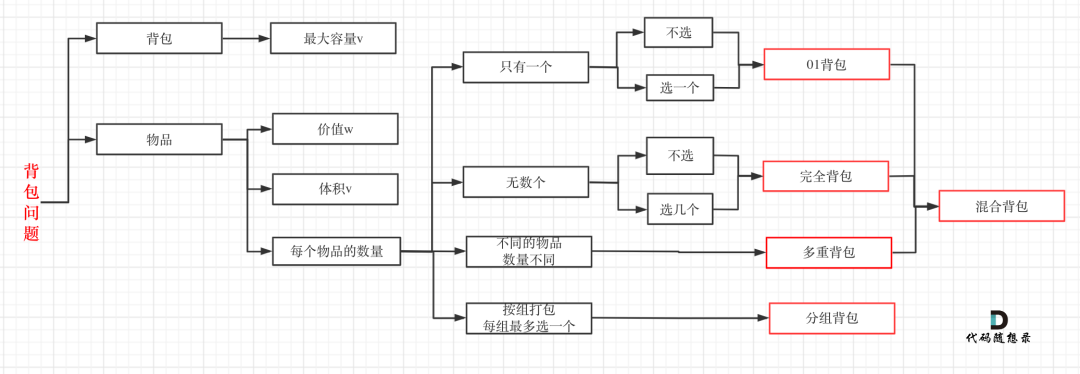
416. Segmentation and subsets 1
As for the other backpacks in the ninth lecture on backpacking, they will hardly be asked in the interview. They are all at the competition level. There is no question of multiple backpacks in leetcode, so the question bank also tells us that 01 backpack and complete backpack are enough.
The complete backpack comes from 01 backpack with a slight change, that is, the number of items in the complete backpack is unlimited.
Therefore, the most important theoretical basis of knapsack problem is 01 knapsack. We must understand it thoroughly!
There are no pure 01 knapsack problems on leetcode. They are all problems in the application of 01 knapsack, that is, they need to be transformed into 01 knapsack problems.
So I'll first explain the principle of 01 knapsack through the pure 01 knapsack problem. Later, when I explain the leetcode problem, the focus is to explain how to transform it into 01 knapsack problem.
Before, some recording friends may have been able to write backpacks skillfully, but as long as you read this article carefully, I believe you will reap unexpected benefits!
01 Backpack
There are n items and a backpack that can carry up to w. The weight of the ith article is weight[i], and the value obtained is value[i]. Each item can only be used once to find out which items are loaded into the backpack and the total value of the items is the largest.

Dynamic programming knapsack problem
This is a standard knapsack problem, so that many students will naturally think of knapsack after reading this. They don't even know how to solve the problem of violence.
In fact, instead of thinking from the bottom up, I habitually think of backpacks. What should be the solution of violence?
Each item actually has only two states, take or not take, so you can use the backtracking method to search all the situations, and the time complexity is o(2^n)
, where n represents the number of items.
So the solution of violence is exponential time complexity. Then we need the solution of dynamic programming to optimize!
In the following explanation, I give an example:
The maximum weight of the backpack is 4.
Items are:
weight | value | |
|---|---|---|
Item 0 | 1 | 15 |
Item 1 | 3 | 20 |
Item 2 | 4 | 30 |
What is the maximum value of the items that can be carried by the backpack?
The figures in the following explanation and illustration take this example as an example.
Two dimensional dp array 01 knapsack
Still a wave of dynamic gauge five part analysis.
- Determine the meaning of dp array and subscript
For the knapsack problem, one way to write it is to use a two-dimensional array, that is, dp[i][j] represents the maximum sum of the value of taking any item from the subscript [0-i] and putting it into the knapsack with the capacity of j.
Just looking at the definition of this two-dimensional array, you will be a little confused. Look at the following figure:
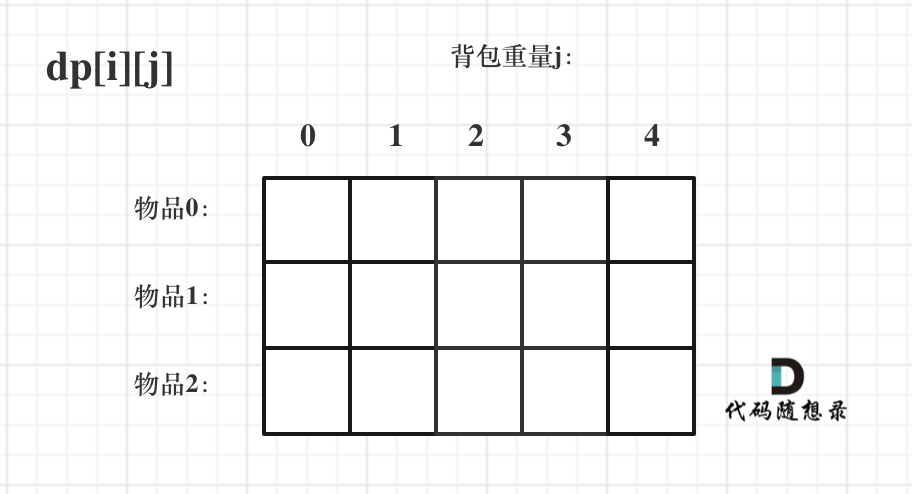
Dynamic programming knapsack problem 1
Always remember the meaning of this dp array. The following steps focus on the meaning of this dp array. If you are confused, let's review what i stands for and what j stands for.
- Determine recurrence formula
Let's review the meaning of dp[i][j]: take any item with subscript [0-i] and put it into the backpack with capacity j. what is the maximum sum of value.
Then it can be pushed out in two directions dp[i][j],
- No item I: launched by dp[i - 1][j], that is, the backpack has a capacity of j, and there is no maximum value of item I in it. At this time, dp[i][j] is dp[i - 1][j]. (in fact, when the weight of item I is greater than the weight of backpack j, item I cannot be put into the backpack, so the value in the backpack is still the same as before.)
- Put item I: launched by dp[i - 1][j - weight[i]], dp[i - 1][j - weight[i]] is the maximum value of not putting item I when the backpack capacity is j - weight[i]. Then dp[i - 1][j - weight[i]] + value[i] (the value of item I) is the maximum value of putting item I in the backpack
So the recursive formula: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
- How to initialize dp array
As for initialization, it must be consistent with the definition of dp array, otherwise it will become more and more chaotic when it comes to recursive formula.
Firstly, starting from the definition of dp[i][j], if the backpack capacity j is 0, that is, dp[i][0], no matter what items are selected, the total value of the backpack must be 0. As shown in the figure:
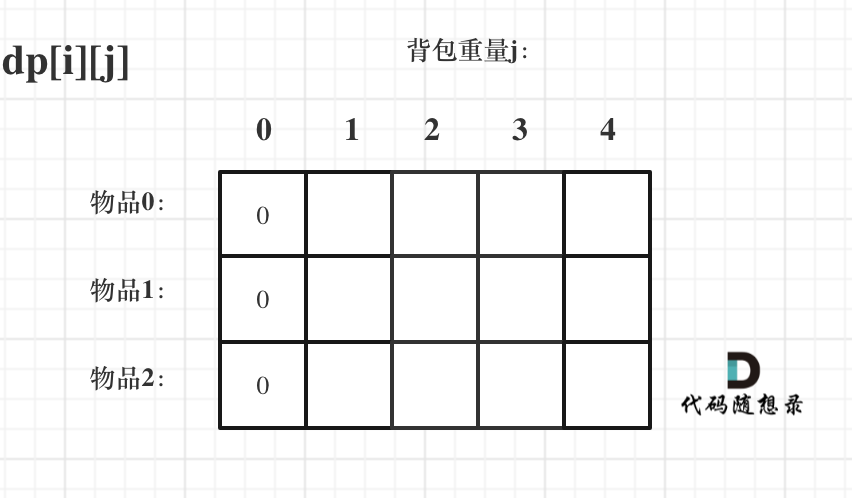
Dynamic programming knapsack problem 2
I'm looking at something else.
State transition equation dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); It can be seen that I is derived from i-1, so it must be initialized when I is 0.
dp[0][j], that is, when i is 0, the maximum value that each capacity backpack can store when storing items with number 0.
So obviously, when J < weight [0], dp[0][j] should be 0, because the backpack capacity is smaller than the weight of the item numbered 0.
When J > = weight [0], dp[0][j] should be value[0], because the capacity of the backpack is enough to put items with number 0.
The initialization code is as follows:
for (int j = 0 ; j < weight[0]; j++) { // Of course, this step can be omitted if the dp array is pre initialized to 0, but many students should not think about it clearly.
dp[0][j] = 0;
}
// Positive order traversal
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
At this time, the initialization of dp array is shown in the figure:
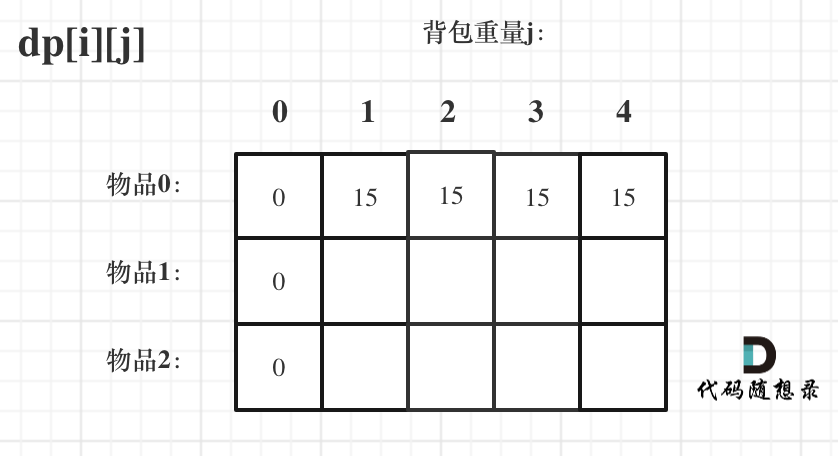
Dynamic programming knapsack problem 7
dp[0][j] and dp[i][0] have been initialized. How many other subscripts should be initialized?
In fact, from the recursive formula: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); It can be seen that dp[i][j] is derived from the upper left value, so the initial values of other subscripts are OK, because they will be overwritten.
Initial - 1, initial - 2, initial 100, all OK!
But it's just that it's more convenient to unify the initial dp array to 0 at the beginning.
As shown in the figure:
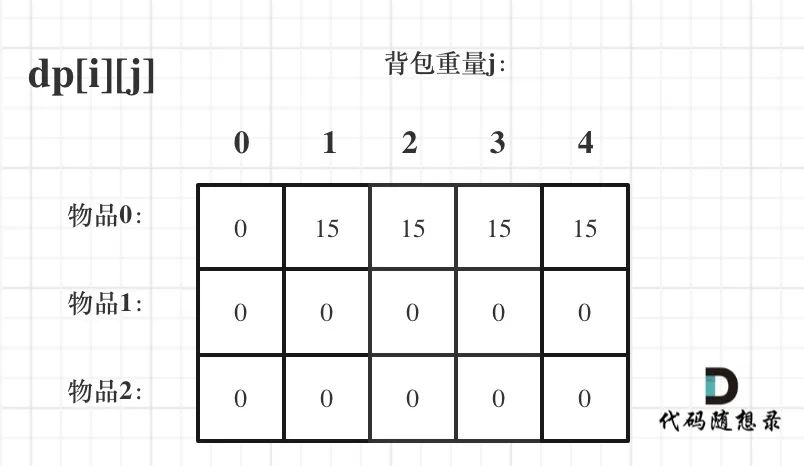
Dynamic programming knapsack problem 10
The final initialization code is as follows:
// Initialize dp
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
It took so much effort to explain how to initialize. I believe many students usually initialize dp array by feeling, but sometimes they don't feel reliable.
- Determine traversal order
As shown in the figure below, there are two traversal dimensions: item and backpack weight
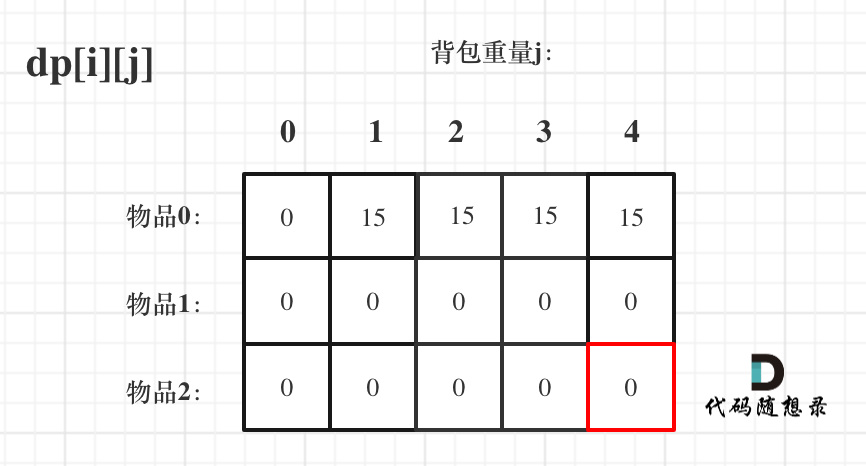
Dynamic programming knapsack problem 3
So the question is, do you traverse the items first or the weight of the backpack first?
In fact, everything is OK!! But it's better to traverse the items first.
Then I first give the code to traverse the items first, and then the weight of the backpack.
// The size of the weight array is the number of items
for(int i = 1; i < weight.size(); i++) { // Traverse items
for(int j = 0; j <= bagweight; j++) { // Traversal knapsack capacity
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
It's OK to traverse the backpack first and then the items! (note the two-dimensional dp array I use here)
For example:
// The size of the weight array is the number of items
for(int j = 0; j <= bagweight; j++) { // Traversal knapsack capacity
for(int i = 1; i < weight.size(); i++) { // Traverse items
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
Why is it possible?
Understand the nature of recursion and the direction of recursion.
dp[i][j] = max(dp[i-1][j], dp[i-1][j - weight[i]] + value[i]); It can be seen from the recursive formula that DP [i] [J] is derived by dp[i-1][j] and dp[i-1][j - weight [i]].
dp[i-1][j] and dp[i-1][j - weight [i]] are in the upper left corner of dp[i][j] (including the positive direction), so the process of traversing items first and then backpacks is shown in the figure:
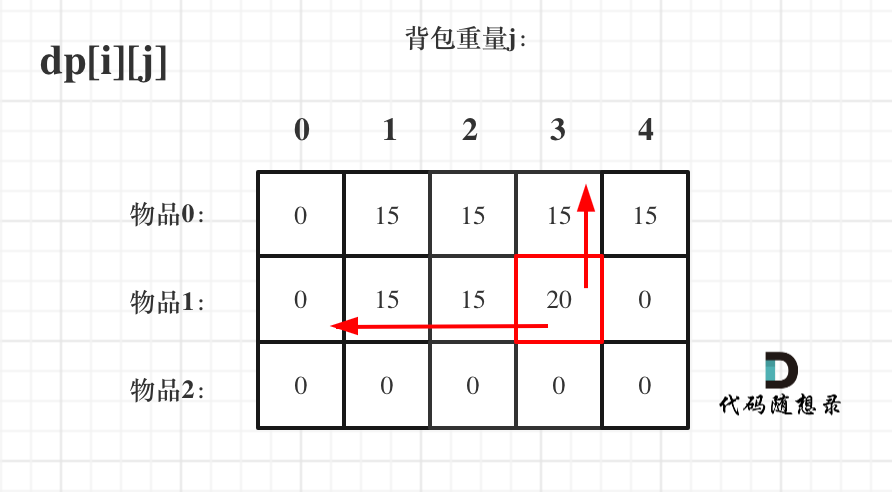
Dynamic programming knapsack problem 5
Let's look at traversing the backpack first and then the items, as shown in the figure:
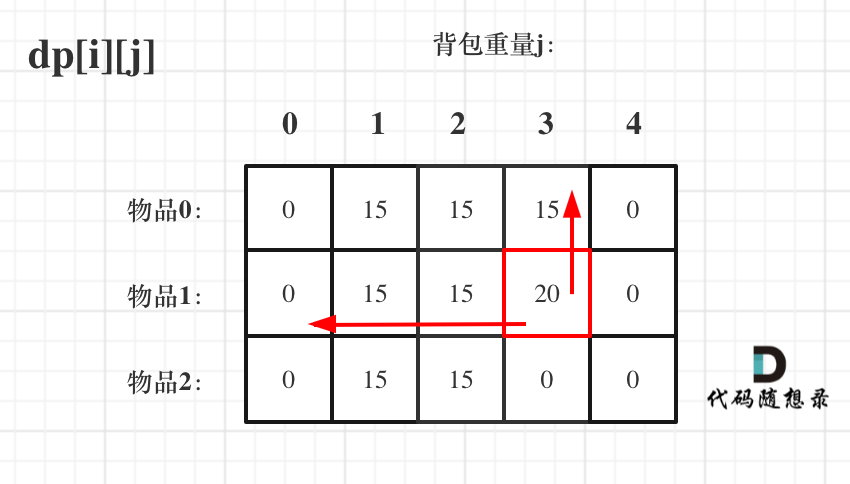
Dynamic programming knapsack problem 6
As you can see, although the order of the two for loops is different, the data required by dp[i][j] is the upper left corner, which does not affect the derivation of dp[i][j] formula at all!
But the order of traversing items first and then backpacks is better understood.
In fact, in the knapsack problem, the sequence of the two for loops is very particular. It is much more difficult to understand the traversal sequence than to understand the derivation formula.
- Derivation of dp array by example
Take a look at the values of the corresponding dp array, as shown in the figure:
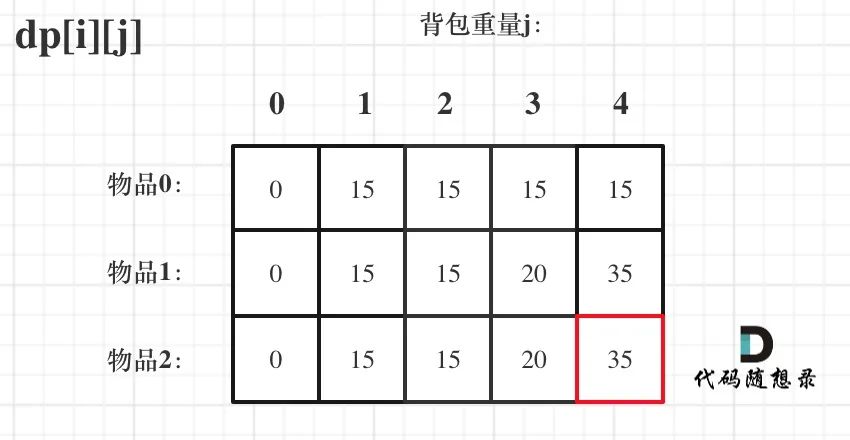
Dynamic programming knapsack problem 4
The end result is dp[2][4].
It is recommended that you deduce it on paper at this time to see if each value in the dp array is like this.
For the topic of dynamic programming, the best process is to give an example on paper, deduce the value of the corresponding dp array, and then write the code!
Many students do dp questions, encounter various problems, and then change things from east to west according to their feelings. No matter how they change them, or they change them in a muddle.
The main reason is that you didn't deduce the evolution process of dp array by yourself. If you understand the derivation, even if there is a problem when you write the code, you can quickly find the problem by printing out the dp array and comparing it with what you deduced.
Complete c + + test code
void test_2_wei_bag_problem1() {
vector<int> weight = {1, 3, 4};
vector<int> value = {15, 20, 30};
int bagweight = 4;
// Two dimensional array
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
// initialization
for (int j = weight[0]; j <= bagweight; j++) {
dp[0][j] = value[0];
}
// The size of the weight array is the number of items
for(int i = 1; i < weight.size(); i++) { // Traverse items
for(int j = 0; j <= bagweight; j++) { // Traversal knapsack capacity
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
cout << dp[weight.size() - 1][bagweight] << endl;
}
int main() {
test_2_wei_bag_problem1();
}
summary
After talking so much, I have just finished talking about the 01 backpack of two-dimensional dp. In fact, you can find that the simplest is the derivation formula. It is estimated that the derivation formula will be written down after reading it, but the difficulty lies in how to initialize and traverse the order.
Maybe some students didn't notice the importance of initialization and traversal order. We will feel it when we buckle the backpack interview questions later.
Let's talk about the difference between the initialization of one-dimensional array and that of two-dimensional array (please talk about the difference between the initialization of one-dimensional array and that of two-dimensional array)!
Other language versions
java
public static void main(string[] args) {
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagsize = 4;
testweightbagproblem(weight, value, bagsize);
}
public static void testweightbagproblem(int[] weight, int[] value, int bagsize){
int wlen = weight.length, value0 = 0;
//Define dp array: dp[i][j] represents the maximum value that the first I items can get when the backpack capacity is j
int[][] dp = new int[wlen + 1][bagsize + 1];
//Initialization: when the backpack capacity is 0, the value that can be obtained is 0
for (int i = 0; i <= wlen; i++){
dp[i][0] = value0;
}
//Traversal order: first traverse the items, and then traverse the backpack capacity
for (int i = 1; i <= wlen; i++){
for (int j = 1; j <= bagsize; j++){
if (j < weight[i - 1]){
dp[i][j] = dp[i - 1][j];
}else{
dp[i][j] = math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);
}
}
}
//Print dp array
for (int i = 0; i <= wlen; i++){
for (int j = 0; j <= bagsize; j++){
system.out.print(dp[i][j] + " ");
}
system.out.print("\n");
}
}
python
def test_2_wei_bag_problem1(bag_size, weight, value) -> int:
rows, cols = len(weight), bag_size + 1
dp = [[0 for _ in range(cols)] for _ in range(rows)]
# Initialize dp array
for i in range(rows):
dp[i][0] = 0
first_item_weight, first_item_value = weight[0], value[0]
for j in range(1, cols):
if first_item_weight <= j:
dp[0][j] = first_item_value
# Update dp array: first traverse the items, and then traverse the backpack
for i in range(1, len(weight)):
cur_weight, cur_val = weight[i], value[i]
for j in range(1, cols):
if cur_weight > j: # Description: the current item cannot be packed on the back
dp[i][j] = dp[i - 1][j] # So don't load the current item
else:
# Define dp array: put the backpack with the capacity of j into the first I items of dp[i][j], and what is the maximum sum of values.
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - cur_weight]+ cur_val)
print(dp)
if __name__ == "__main__":
bag_size = 4
weight = [1, 3, 4]
value = [15, 20, 30]
test_2_wei_bag_problem1(bag_size, weight, value)
go
func test_2_wei_bag_problem1(weight, value []int, bagweight int) int {
// Define dp array
dp := make([][]int, len(weight))
for i, _ := range dp {
dp[i] = make([]int, bagweight+1)
}
// initialization
for j := bagweight; j >= weight[0]; j-- {
dp[0][j] = dp[0][j-weight[0]] + value[0]
}
// Recurrence formula
for i := 1; i < len(weight); i++ {
//Positive or reverse order
for j := weight[i];j<= bagweight ; j++ {
dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i])
}
}
return dp[len(weight)-1][bagweight]
}
func max(a,b int) int {
if a > b {
return a
}
return b
}
func main() {
weight := []int{1,3,4}
value := []int{15,20,30}
test_2_wei_bag_problem1(weight,value,4)
}
javascript
function testweightbagproblem (wight, value, size) {
const len = wight.length,
dp = array.from({length: len + 1}).map(
() => array(size + 1).fill(0)
);
for(let i = 1; i <= len; i++) {
for(let j = 0; j <= size; j++) {
if(wight[i - 1] <= j) {
dp[i][j] = math.max(
dp[i - 1][j],
value[i - 1] + dp[i - 1][j - wight[i - 1]]
)
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
// console.table(dp);
return dp[len][size];
}
function testWeightBagProblem2 (wight, value, size) {
const len = wight.length,
dp = Array(size + 1).fill(0);
for(let i = 1; i <= len; i++) {
for(let j = size; j >= wight[i - 1]; j--) {
dp[j] = Math.max(dp[j], value[i - 1] + dp[j - wight[i - 1]]);
}
}
return dp[size];
}
function test () {
console.log(testWeightBagProblem([1, 3, 4, 5], [15, 20, 30, 55], 6));
}
test();