This blog takes you to understand the storage of C language shaping and floating point in memory. Through this blog, we will have a further understanding of memory.
1, Review data types
We have already learned about the built-in data types in C language:
char //Character data types, such as a, b, c! Equal character short //Short integers are used to describe integers with a smaller range int //Shaping is used to describe integers long //Long integers are used to describe a wider range of integers long long //A longer integer is used to describe a wider range of integers float //Single precision floating-point numbers are used to describe decimals double //Double precision floating-point numbers have higher precision than float
The so-called built-in type is the type of C language itself. In addition, there are user-defined types, such as structures.
The meaning of these built-in types:
- Use this type to open up the size of memory space (the size of memory space determines the scope of use).
- Determines how to view memory space (for example, the storage of integer 5 and floating point 5.0 in memory is different).
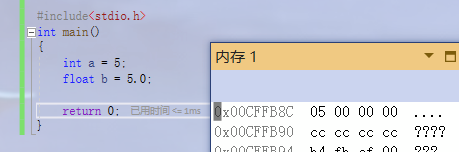
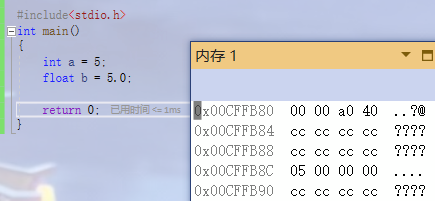
As you can see, the storage methods of integer and floating point are different.
1.1 basic classification of types
- plastic
char//The storage of characters in memory is ASCII code value, which is also an integer, so char is classified as integer unsigned char signed char short unsigned short [int] signed short [int] int unsigned int signed int long unsigned long [int] signed long [int]
Used means unsigned and signed means signed. The highest bit of unsigned type is not a sign bit. Therefore, unsigned type can only represent unsigned numbers (which can be understood as positive integers), and the range of positive integers is larger than that of signed type.
- float
float double
- Construction type
> Array type //Int a [10] int b [5] char c [5] these three arrays are different array types > Structure type struct > Enumeration type enum > Union type union
- Pointer type
int* pi; char* pc; float* pf; void* pv;
- Empty type
void indicates an empty type (no type)
It is usually applied to the return type of the function, the parameter of the function (if the parameter of the function is void, the parameter cannot be passed), and the pointer type (pointer without specific type)
2, Shaping storage in memory
When a variable is created, it is necessary to open up space in memory. The size of the opened memory space depends on the data type of the variable.
If we create two shaping variables:
int main()
{
int a=16;
int b=-16;
return 0;
}
They are stored in memory as follows:
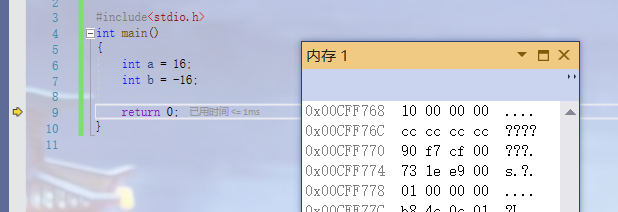
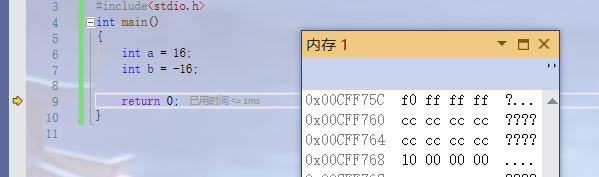
To explain the difference between the two variables, first review the original code, inverse code and complement code:
2.1 original code, inverse code and complement code
There are three representations of symbolic shaping in computer, namely original code, inverse code and complement code. (unsigned numbers also have three forms of original inverse complement, but their original inverse complement is the same)
The three representation methods have two parts: symbol bit and numerical bit. Generally, the highest bit is used to represent the symbol bit. The symbol bit is 0 to represent "positive" and 1 to represent "negative", while the three representation methods of numerical bit are different.
Original code
The original code is the binary representation of an integer.
Inverse code
Inverse code means that the sign bit of the original code remains unchanged, and other bits are reversed by bit (0 becomes 1, 1 becomes 0)
Inverse code
The complement is to add 1 to the inverse code
Therefore, the original inverse complement of variables a and b above is as follows:
int a=16; 00000000000000000000000000010000 The original code, inverse code and complement code are the same int a=-16; Original code: 10000000000000000000000 The leftmost 1 means negative. Inverse code: 11111111111111111111111111111101111 Complement: 11111111111111111111111111111110000
The data is stored in the form of hexadecimal complement (why it exists in the form of complement, which was explained in the chapter operators and expressions earlier), so their storage methods should be 00 00 10 and FF F0, but the compiler stores them upside down, which involves the concept of size end:
2.2 large and small ends
There are two ways of computer storage:
Large end (storage) mode means that the low bit of data is saved in the high address of memory, while the high bit of data is saved in the low address of memory;
Small end (storage) mode means that the low order of data is saved in the low address of memory, while the high order of data is saved in the high address of memory.
For example, 0x12345678 data:
Big end storage:
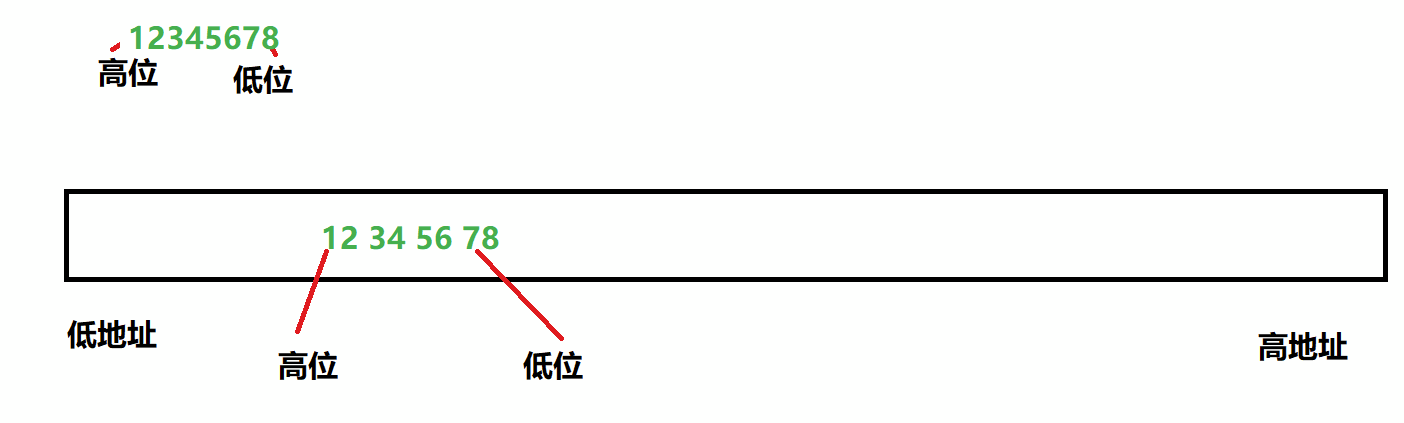
Small end storage:
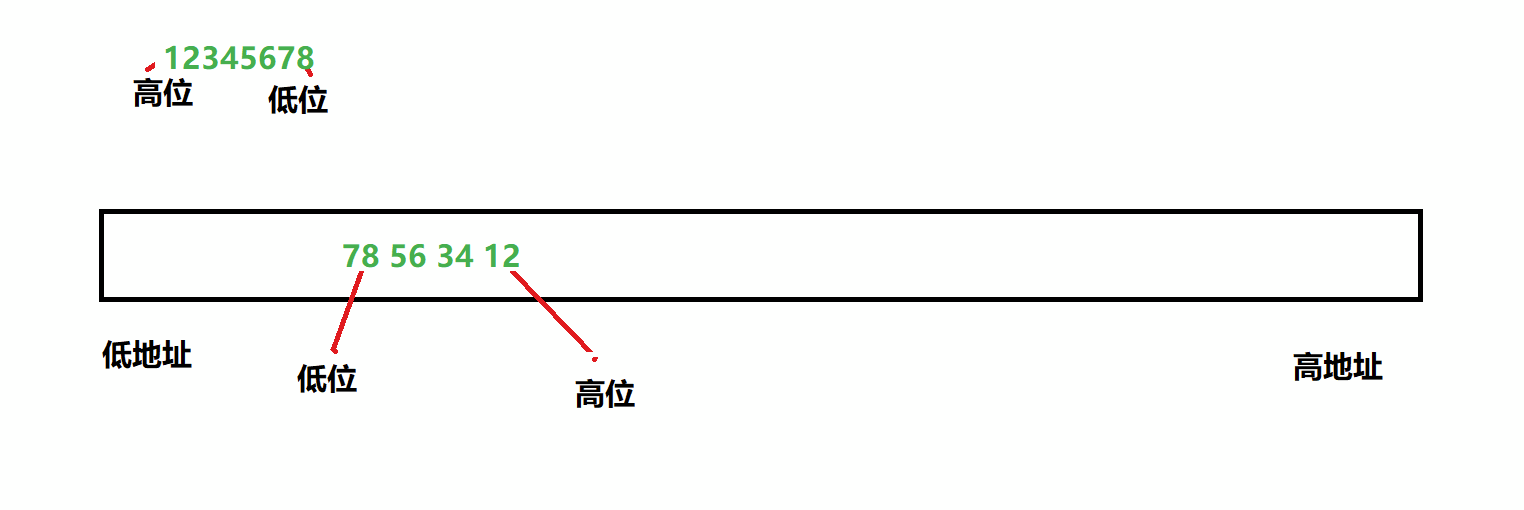
2.2.1 why are there large and small ends?:
The big and small ends are also called big end byte order storage mode and small end byte order storage mode, so the difference between the big and small ends is actually the storage mode of variable byte order.
In the computer system, we take bytes as the unit. Each address unit corresponds to a byte, and one byte is 8bit. However, in C language, in addition to the 8-bit char, there are also 16 bit short and 32-bit long (depending on the specific compiler). In addition, for processors with more than 8 bits, such as 16 bit or 32-bit processors, since the register width is greater than one byte, there must be a problem of arranging multiple bytes. Therefore, it leads to large end storage mode and small end storage mode.
For example, for a 16bit short x, the address in memory is 0x0010, and the value of X is 0x1122, then 0X11 is the high byte and 0x22 is the low byte. For the big end mode, put 0X11 in the low address, that is, 0x0010, and 0x22 in the high address, that is, 0x0011. Small end mode, just the opposite. Our commonly used X86 structure is the small end mode, while KEIL C51 is the large end mode. Many arm and DSP are in small end mode. Some ARM processors can also be selected by hardware whether it is large end mode or small end mode.
These two methods have their own advantages and disadvantages:
Small end mode: the byte content does not need to be adjusted for forced data conversion. The storage methods of 1, 2 and 4 bytes are the same, such as converting int type to char type.
Big end mode: the determination of symbol bit is fixed as the first byte, which is easy to determine positive and negative.
Therefore, there is no difference between the two methods, but different storage methods are used in different places. For example, the measurement unit has British metric system, and the car has left-hand and right-hand steering. At the beginning, there is no unified standard, so we have to use both tracks. At first, it should be that each has its own advantages in hardware implementation, so it has been used.
2.2.2 judge the byte order (size end) of the machine with code:
For a variable a=1, if it is a large end, its low address stores 00. If it is a small end, its low address stores 01. Therefore, we only need to get the value of the low address and judge it. We can forcibly convert the address of a into a char * pointer, and then dereference to get the content of the low address (char * pointer dereference can only access one byte):
#include <stdio.h>
int check_sys()
{
int i = 1;
return (*(char*)&i);
}
int main()
{
int ret = check_sys();
if (ret == 1)
{
printf("Small end\n");
}
else
{
printf("Big end\n");
}
return 0;
}
3, Some exercises on data type storage
- Output of the following program
#include <stdio.h>
int main()
{
char a= -1;
signed char b=-1;
unsigned char c=-1;
printf("a=%d,b=%d,c=%d",a,b,c);
return 0;
}
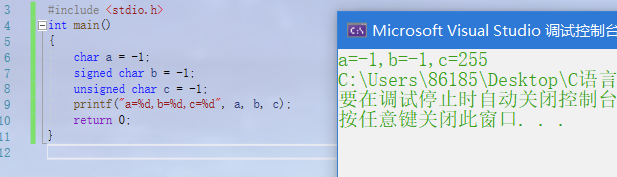
char a=-1; first-1 Is an integer, its size is 4 bytes, that is, 32 bits, 100000000000000000001 Its complement is 111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111 however a yes char Type, variable of this type a It can only store 1 byte, that is, 8 bits: 11111111 Similarly signed char b=-1; signed char Type b Only 8 bits can be stored: 11111111 unsigned char c=-1; unsigned char Type c Only 8 bits can be stored: 11111111 When printing, it needs to be improved, a and b Complement symbol bit. The complement after shaping and lifting is: 11111111111111111111111111111111111111111 The result after printing the original code is-1 c It is unsigned, and the high bit is not a symbol bit. Therefore, the high bit is filled with 0 after shaping and lifting, and the complement after shaping and lifting is: 0000000000000000000000011111111,Since the high order is 0, it is a positive number. The original inverse complement is the same, and the printed result of the original code is 255
- The following program outputs:
#include <stdio.h>
int main()
{
char a = -128;
printf("%u\n",a);//%u print unsigned decimal numbers
return 0;
}
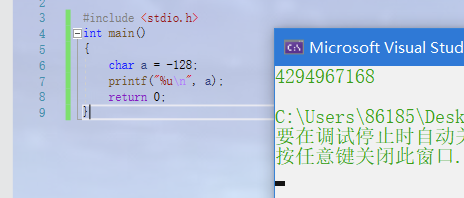
-128 Is an integer. Its size is 4 bytes, that is, 32 bits, 10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 Its complement is 11111111111111111111111111111111111110000000 char a 10000000 stored in When printing a Occurrence of shaping lifting: 11111111111111111111111110000000 Prints as an unsigned number, so the compiler thinks a The complement after shaping and lifting is the same as the original code, so it is printed directly in decimal form 11111111111111111111111110000000,The final result is 4294967168
#include <stdio.h>
int main()
{
char a = 128;
printf("%u\n", a);
return 0;
}
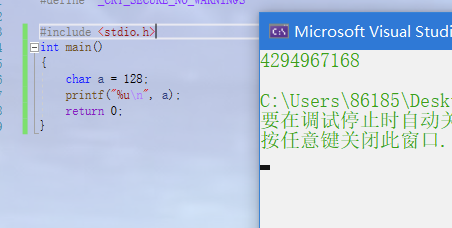
128=127+1 127 The storage form of is 00000000000000000001111111 +1 After that, it will be 0000000000000000000000000000000000000000 char a 10000000 in storage Therefore, the results of this program and char a=-128 The results are the same
It is not difficult to find that since the char type variable has only 8 bytes and the highest bit also represents the symbol bit, the numerical bit of char type has only 7 bits, so the range that char type can represent is - 128 ~ 127:

If you set 127 + 1, it will directly become - 128, and - 1 + 1 will become 0, so the following closed loop will be formed:
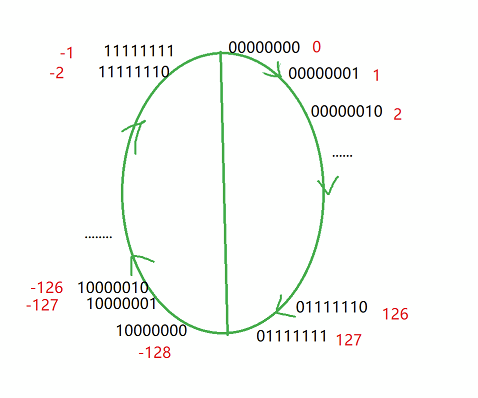
So the third question above is not difficult to understand. After 127 + 1, you will get - 128
#include <stdio.h>
int main()
{
int i = -20;
unsigned int j = 10;
printf("%d\n", i + j);
return 0;
}
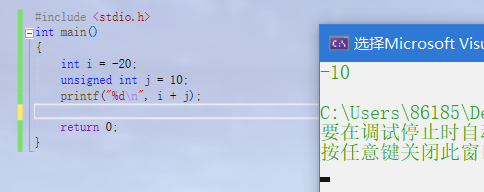
Adding the complements of i and j, and then converting the result into the original code is the final result
#include <stdio.h>
#include<Windows.h>
int main()
{
unsigned int i;
for (i = 9; i >= 0; i--)
{
printf("%u\n", i);
Sleep(1000);
}
return 0;
}
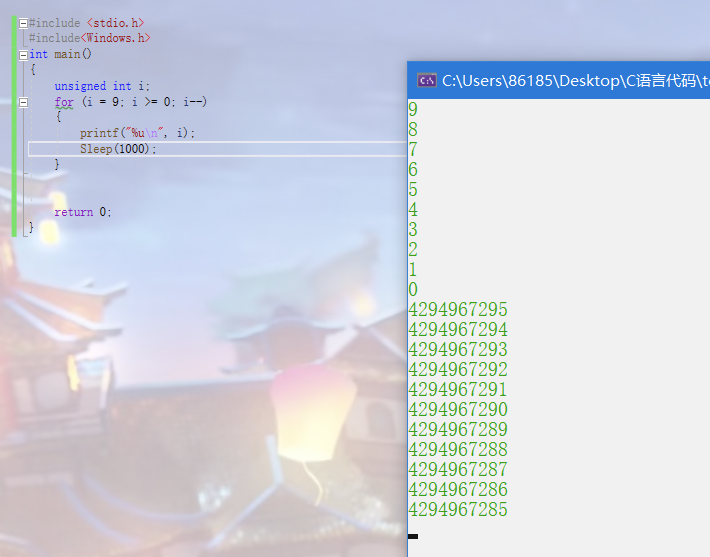
Since i is an unsigned number, i > = 0 is always true, so the program will loop.
#include<stdio.h>
#include<string.h>
int main()
{
char a[1000];
int i;
for (i = 0; i < 1000; i++)
{
a[i] = -1 - i;
}
printf("%d", strlen(a));
return 0;
}
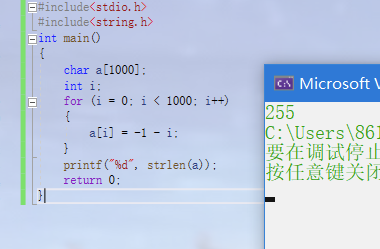
A is a character array with elements ranging from - 128 to 127. Therefore, after the for loop, the contents of a are:
-1,-2,-3,-4,........-127,-128,127,126,......2,1,0,-1,-2......
Since this is a character array and the ASCII value '\ 0' of 0 is the same, strlen calculates the length of the characters before 0, that is, the length of - 1 ~ 1, so the result is 255
#include <stdio.h>
unsigned char i = 0;
int main()
{
for (i = 0; i <= 255; i++)
{
printf("hello world\n");
}
return 0;
}
The result is an endless loop because the range of unsigned char i is 0 ~ 255255 + 1 = 0
4, Storage of floating point numbers in memory
According to the international standard IEEE 754, any binary floating-point number V can be expressed in the following form:
(-1)^s * M * 2^E
(- 1)^s represents the sign bit. When s=0, V is a positive number; When s=1, V is negative.
M represents a significant number, greater than or equal to 1 and less than 2.
2^E indicates exponential bit
For example: decimal 5.0, written in binary, is 101.0, equivalent to 1.01 × 2^2 . Then, according to the format of V above, we can get s=0,
M=1.01,E=2.
Decimal - 5.0, written as binary is - 101.0, equivalent to - 1.01 × 2^2 . Then, s=1, M=1.01, E=2.
IEEE 754 stipulates that for 32-bit (4 bytes) floating-point numbers, the highest 1 bit is the symbol bit s, the next 8 bits are the exponent E, and the remaining 23 bits are the significant number M.

For 64 bit floating-point numbers, the highest bit is sign bit S, the next 11 bits are exponent E, and the remaining 52 bits are significant digits M.
IEEE 754 has some special provisions for the significant number m and index E. As mentioned earlier, 1 ≤ m < 2, that is, M can be written as 1 The form of xxxxxx, where xxxxxx represents the decimal part.
IEEE 754 stipulates that when saving M in the computer, the first digit of this number is always 1 by default, so it can be rounded off and only the following xxxxxx part is saved.
For example, when saving 1.01, only 01 is saved. When reading, add the first 1. The purpose of this is to save 1 significant digit.
Take the 32-bit floating-point number as an example. There are only 23 bits left for M. after rounding off the 1 of the first bit, it is equivalent to saving 24 significant digits.
The case of index E is more complex
Firstly, E is an unsigned int, which means that if E is 8 bits, its value range is 0 ~ 255; If E is 11 bits, its
The value range is 0 ~ 2047. However, we know that E in scientific counting can be negative, so IEEE 754 stipulates that e is true when stored in memory
The real value must be added with an intermediate number, which is 127 for 8-bit E; For an 11 bit e, the median is 1023. For example, e of 2 ^ 10 is 10, so when saving as a 32-bit floating-point number, it must be saved as 10 + 127 = 137, that is, 10001001.
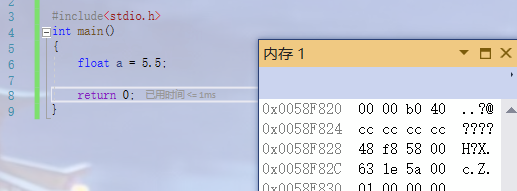
Now we know how floating point numbers are stored in memory. Take floating point number 5.5 for example:
5.5 Written in binary form is 101.1(1 of the decimal represents 2^(-1)That is 0.5) finish writing sth.(-1)^s * M * 2^E Form of: (-1)^0*1.011*2^2 therefore S=0 M=1.011 E=2 therefore S 0 in memory E Save 2 in memory+127=129 M Save 011 After they wrote binary: 0 10000001 01100000000000000000000 This 32-bit binary number is obtained after merging: 01000000101100000000000000000000 Convert this string of binary numbers to hexadecimal: 0x40b00000 The memory is small end storage, so it is stored as 0000b040
When E is taken out of memory, there are three situations:
- E is not all 0 or all 1 (normal)
At this time, the floating-point number is represented by the following rule, that is, subtract 127 (or 1023) from the calculated value of index E to obtain the real value, and then add the first 1 before the significant number M. For example, the binary form of 0.5 is 0.1. Since it is specified that the positive part must be 1, that is, if the decimal point is shifted to the right by 1 digit, it will be 1.0 * 2 ^ (- 1), and its order code is - 1 + 127 = 126, which means 01111110, while the mantissa of 1.0 is 0 after removing the integer part and complementing 0 to 23 digits, then its binary form is:
0 01111110 00000000000000000000000
- E is all 0
If e is all 0, it means that the original value of E is - 127 or - 1023. This number is super small, and the precision of float and double cannot represent this number
At this time, the exponent E of the floating point number is equal to 1-127 (or 1-1023), which is the real value, and the significant number M is no longer added with the first 1, but restored to 0 The decimal of XXXXXX. This is done to represent ± 0 and small numbers close to 0.
- E is all 1
If e is all 1, the original value of E is 128. This number is super large, and the precision of float and double cannot represent this number
At this time, if the significant digits M are all 0, it means ± infinity (the positive and negative depend on the sign bit s);
So look at the following procedure:
#include<stdio.h>
int main()
{
int n = 9;
float* pFloat = (float*)&n;
printf("n The value of is:%d\n", n);
printf("*pFloat The value of is:%f\n", *pFloat);
*pFloat = 9.0;
printf("num The value of is:%d\n", n);
printf("*pFloat The value of is:%f\n", *pFloat);
return 0;
}
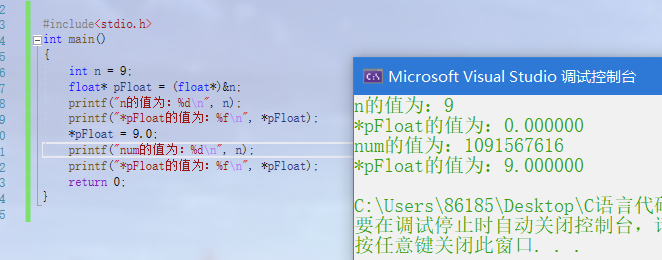
After n is converted into a float * pointer and then dereferenced, it is printed according to the memory form of float: split the binary form of n 0000000000000000000000000000001001 to obtain the first sign bit s=0, the index E=00000000 in the next 8 bits, and the last 23 significant digits M = 000 0000001001. Since the index E is all 0, it conforms to the second case in the previous section. Therefore, the floating-point number V is written as: V=(-1)^0 × 0.00000000000000000001001 × 2(-126)=1.001 × 2 (- 146) obviously, V is a small positive number close to 0, so it is 0.000000 in decimal.
Floating point number 9.0 is equal to binary 1001.0, i.E. 1.001 × 2^3. Then, the sign bit of the first bit s=0, the significant number M is equal to 001, followed by 20 zeros to fill 23 bits, and the index E is equal to 3 + 127 = 130, i.E. 10000001. Therefore, written in binary form 0100000100000000000000000000000, this 32-bit binary number is reduced to decimal, which is 1091567616.