1. Linearity table
linear list is a finite sequence of n data elements with the same characteristics. It is a data structure widely used in practice. The common linear lists are: sequential list, linked list, stack, queue, string
A linear table is logically a linear structure, that is, a continuous straight line. However, the physical structure is not necessarily continuous. When the linear table is stored physically, it is usually stored in the form of array and chain structure.
Array storage
It can be stored completely or there can be space left
Store in chain structure
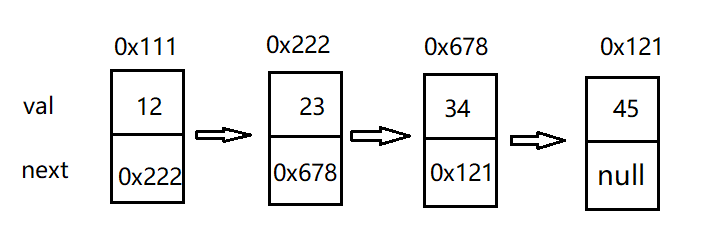
This is a simple single linked list (one-way headless acyclic linked list). The specific structure will be introduced in detail later.
2. Sequence table
2.1 concept and structure
Data structure: describes how data is organized.
A sequence table is a data structure. Its bottom layer is an array.
Sequential table is a linear structure in which data elements are sequentially stored in a storage unit with continuous physical addresses. Generally, array storage is used to complete the addition, deletion, query and modification of data on the array.
In order to better understand the sequence table, the following figure can help you better understand it.
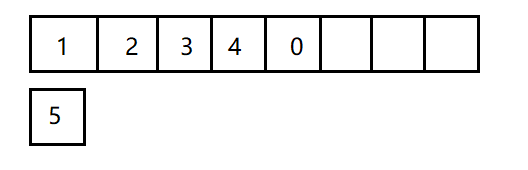
The upper row indicates where data is stored, while the lower row indicates the number of data in the linked list.
The sequence table can generally be divided into:
- Static sequential table: use fixed length array storage.
- Dynamic sequential table: use dynamic array storage.
The static sequence table is suitable for determining the scenario that knows how much data needs to be stored. The fixed length array of static sequence table leads to large N, waste of space and insufficient space.
In contrast, the dynamic sequential table is more flexible and dynamically allocates space according to needs.
2.2 interface implementation
In the above, we use icons to show the sequence table. In Java, we should construct these things according to this idea to let the JVM know what the code we write represents.
Next, we will implement the interface of the sequence table. The following is the code:
import java.util.Arrays;
public class MyArrayList {
public int[] elem;//Array reference type (on heap) to store data
public int usedSize;//Number of valid data
public MyArrayList() {//Initializing an array with a constructor
this.elem = new int[5];//Let this Elem equals the new integer array
}
}
-In the above code, we first created elme, which is used to open up space on the heap and store arrays;
-Then we create usedSize, which is used to record how many data there are in the sequence table.
-Then we use the constructor to initialize the array so that the array can be stored in the sequence table.
Interface 1: add an element at a certain position in the sequence table
//Add new element in pos position
public void add(int pos, int data) {
//1. Judge whether the array is full
if (isFull()) {
System.out.println("The sequence table is full! Capacity expansion required!");
this.elem = Arrays.copyOf(this.elem,2*this.elem.length);//The expanded array still has to be assigned to the original this elem
//return;
}
//2. First judge the legitimacy of pos location
if (pos < 0 || pos > this.usedSize) {
System.out.println("pos Illegal location!!!");
return;
}
//3. Move the element from back to front. If pos==usedSize, put it directly to the usedSize position
if (pos == this.usedSize) {
this.elem[pos] = data;
this.usedSize++;
return;
}
for (int i = this.usedSize - 1; i >= pos; i--) {
this.elem[i + 1] = this.elem[i];
}
this.elem[pos] = data;
this.usedSize++;
}
public boolean isFull() {
if (this.usedSize == this.elem.length) {
return true;
}
return false;
}
When we add elements to the sequence table, we can fill them or have vacancies. When the number of added elements is greater than its space, we can expand the capacity. After capacity expansion, the expanded table should be assigned back to the original table.
In this way, our interface for inserting data into the sequence table is established. In order to check whether it is correct, we also need to create a printing method to check whether the inserted data conforms to our design idea.
Note: when inserting elements in the sequence table, there must be elements in front of the insertion position, otherwise it is illegal!!!
Interface 2: printing method
// Print sequence table
public void display() {
for (int i = 0; i < this.usedSize; i++) {
System.out.print(this.elem[i]+" ");
}
System.out.println();
}
The idea of printing is the same as that of printing the elements in the array. We can see that the introduction of usedSize can greatly improve the efficiency of the code, rather than re writing the code to obtain how many data there are in the sequence table.
After these two preparations are made, we can check whether we have correctly inserted data in the main function.
public static void main(String[] args) {
MyArrayList myArrayList = new MyArrayList();
myArrayList.add(0,1);
myArrayList.add(1,2);
myArrayList.add(2,3);
myArrayList.add(3,4);
myArrayList.display();
}
//Output: 1,2,3,4
First of all, you have to instantiate the class where the call sequence table is located. Because the array is stored in the sequence table, its starting position starts from 0, which should be noted.
Interface 3: judge whether the sequence table contains an element
// Determines whether a toFind element is included
public boolean contains(int toFind) {
for (int i = 0; i < this.usedSize; i++) {
if(this.elem[i] == toFind) {
return true;
}
}
return false;
}
Idea: use the for loop to traverse the sequence table.
Interface 4: find the corresponding position of an element
// Find the location of an element
public int search(int toFind) {
for (int i = 0; i < this.usedSize; i++) {
if(this.elem[i] == toFind) {
return i;
}
}
return -1;
}
Idea: use the for loop to traverse the sequence table. If found, return the subscript of the location of the element. If not found, return - 1, because the subscript of the sequence table is the same as that of the array, which starts from 0 by default.
Interface 5: get the element of a location
//Gets the element of the pos location
public int getPos(int pos) {
//1. Judge whether the sequence table is empty
if(this.isEmpty()) {
return -1;
}
//2. Illegal POS
if(pos < 0 || pos >= this.usedSize) {
return -1;//-1 is used to mark that the current position is illegal
}
//3. Return the element at that location
return this.elem[pos];
}
public boolean isEmpty() {
/*if(this.usedSize == 0) {
return true;
}
return false;*/
return this.usedSize == 0;
}
Idea:
- First, we have to judge whether the sequence table is empty;
- Next, judge whether the obtained position conforms to the sequence table we created;
- If the above two conditions are reasonable, the data can be returned directly.
Interface 6: setting elements for a location
//The element at pos position is set to value
public void updatePos(int pos, int value) {
//1. Judge whether the sequence table is empty
if(this.isEmpty()) {
return;
}
//2. Illegal POS
if(pos < 0 || pos >= this.usedSize) {
return;
}
//3. Set value
this.elem[pos] = value;
}
Idea:
- First, you have to judge whether the sequence table is empty;
- Secondly, judge the legitimacy of the location of the updated data;
- If the above two conditions are reasonable, you can set the element directly.
Interface 7: delete the first keyword key
//Delete the keyword key that appears for the first time
public void remove(int key) {
int index = search(key);//Find the keyword and return its subscript
if(key == -1) {
System.out.println("Keywords you want to delete:"+key+"non-existent!!");
return;
}
for (int i = index; i < this.usedSize-1; i++) {//When i move, i can't move back after i move the last number, so i have to set a reasonable condition i < this usedSize-1
this.elem[i] = this.elem[i+1];
}
this.usedSize--;
}
Idea:
- First, we have to find the location of this keyword with the help of interface 4;
- Secondly, judge the legitimacy of location;
- Finally, directly move the data behind the keyword forward to complete the deletion. At the same time, the usedSize value also needs to be changed accordingly.
The data of the deletion sequence table can be understood as follows:
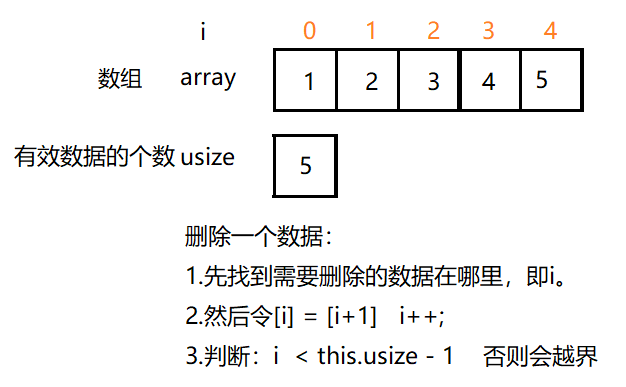
Other interfaces: get the length of the table and clear the sequence table
// Get sequence table length
public int size() {
return usedSize;
}
// Empty sequence table
public void clear() {
this.usedSize = 0;
}
Question:
- The time complexity of inserting and deleting sequence tables is O(N)
- Capacity expansion requires applying for new space, copying data and releasing old space, which will consume a lot.
- The capacity increase is generally double, which is bound to waste some space.
Based on the above shortcomings, we introduce linked list.
3. Linked list
3.1 concept and structure of linked list
Linked list is a discontinuous storage structure in physical storage structure. The logical order of data elements is realized through the reference link order in the linked list. Generally speaking, a linked list is connected by nodes.
Classification of linked list:
In practice, the structure of linked list is very diverse. There are eight linked list structures when the following situations are combined:
- Unidirectional and bidirectional
- Take the lead, don't take the lead
- Cyclic and non cyclic
Next, we introduce a one-way non leading acyclic linked list, that is, single linked list.
The linked list is formed by connecting nodes. The node structure is as follows:
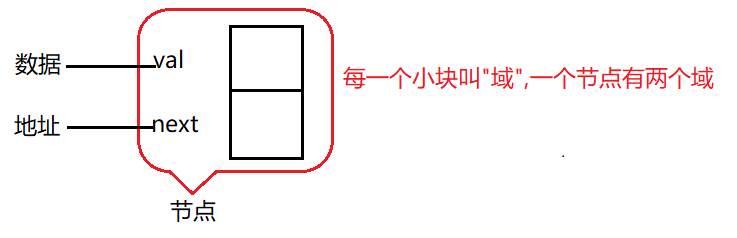
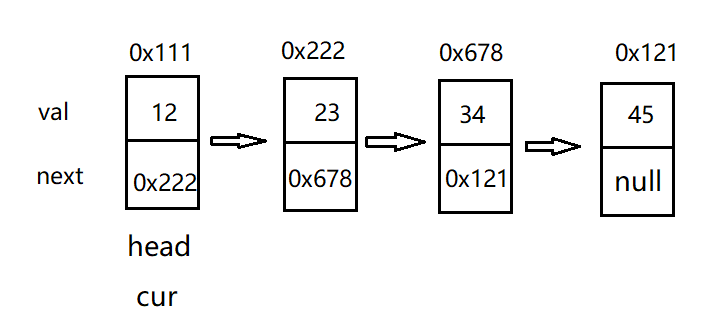
We can see that a node has two fields, one is data and the other is address. The single linked list is connected by such nodes.
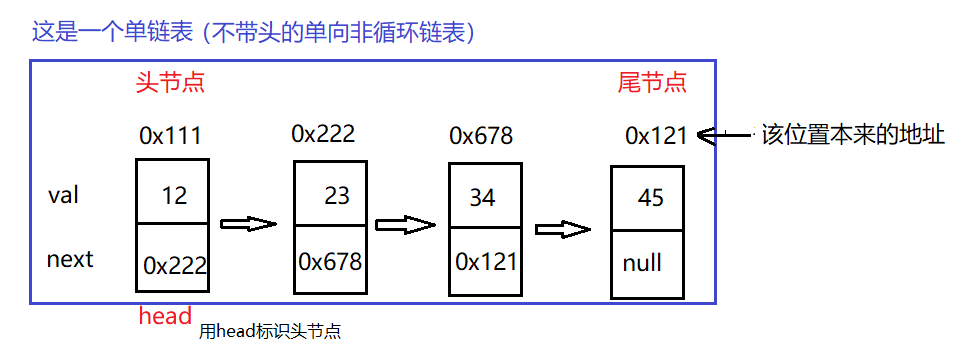
As can be seen from the above figure:
- Each node of the single linked list has two fields, the upper part is data, and the lower part is a reference (address) to the next node;
- The first node is the head node and the last node is the tail node;
- Each node has a reference (address);
- Nodes are connected through next.
By comparing the graph structure of sequence list and linked list, we can see that sequence list is physically and logically continuous; The linked list is not necessarily continuous physically, but must be continuous logically.
The above figure shows a headless single linked list. Next, let's look at a single linked list of leading nodes
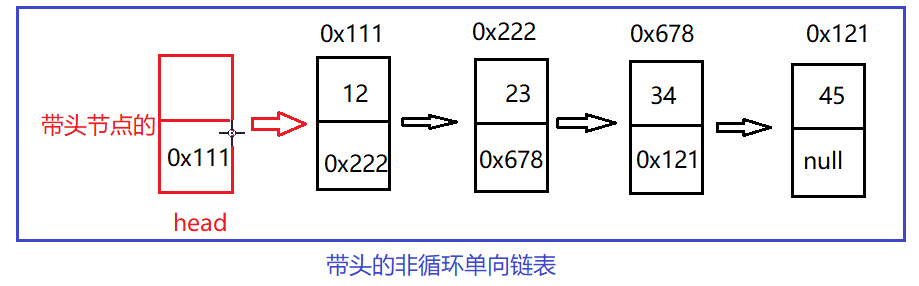
It has a header node, but the header node does not store data. In the next study, we first get familiar with the single linked list without taking the lead. On this basis, we get familiar with the linked list.
Supplement:
Circular linked list:
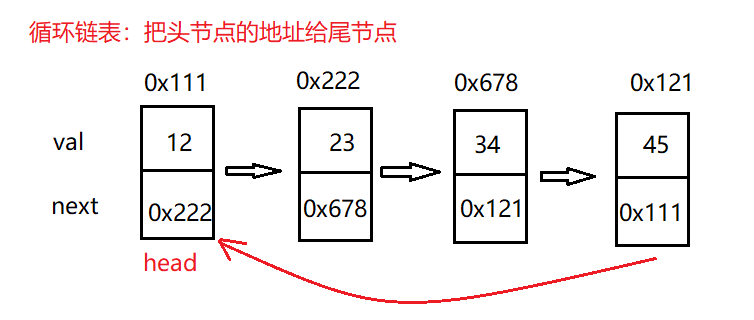
Linked list:
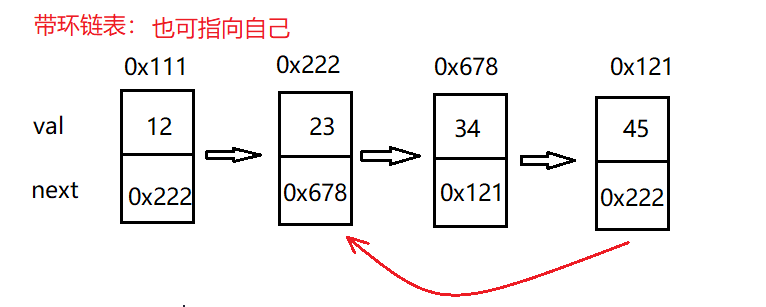
3.2 implementation of linked list
3.2. 1 implementation of headless one-way linked list
In order to implement a single linked list, we need to define a Node node in the code, which is also a class. In this class, we need to specify two parts, one is data, and the other represents the address of the next Node; Then, the construction method is used to instantiate the data of each Node. The code can be written as:
//Node is a class
class Node {//Defines a node that has two values
public int val;//Integer data
public Node next;//Address of the next node
public Node(int val) {
this.val = val;
}
}
Then we create a linked list class, in which we can call the properties of the node.
First define a header node, and then insert data into the linked list by enumeration. The code is as follows:
public class MyLinkedList {//Single linked list
public Node head = null;
//Create a single linked list in an exhaustive way
public void creatList() {
Node node1 = new Node(1);
Node node2 = new Node(2);
Node node3 = new Node(3);
Node node4 = new Node(4);
node1.next = node2;
node2.next = node3;
node3.next = node4;
this.head = node1;
}
}
In the above code, we call the Node class and instantiate four objects, and then make the reference of each object point to the reference of the next Node. In this way, nodes are connected.
Then, in the class MyLinkedList, in order to check whether the data of the linked list is instantiated successfully, we have to create a printing function:
Interface 1: print function
public void show() {
/*while (this.head != null) {//Disadvantages of this method: the value saved in the last head is null, that is, the head is missing
System.out.println(this.head.val);
this.head = this.head.next;*/
Node cur = this.head;//It can ensure that the head is always in front. Moving only cur
while (cur != null) {
System.out.print(cur.val+ " ");
cur = cur.next;
}
System.out.println();
}
The printing function can be written as the above two, but the second one is preferred. We can see from the print function in the note that the head is used to traverse the whole linked list. After traversing the linked list, the head is at the back, which is inconsistent with our design concept. Therefore, in the following code, we define a new node cur to traverse the array instead of the head node. In this way, the rationality of the code is improved.
Through the above two interfaces, we can completely create a linked list, but the method is too low. If a large amount of data needs to be inserted into the linked list, the efficiency of the code will be reduced, so we have this method to establish the linked list. Plug in:
Interface 2: head insertion method
As the name suggests, the head insertion method is to insert nodes from the head of the linked list, and each newly inserted node is the head node of the linked list.
//● head insertion method
public void addFirst(int val) {
Node node = new Node(val);//The first step is to define the data to be inserted
node.next = this.head;//Step 2
this.head = node;//It can ensure that the head does not move
}
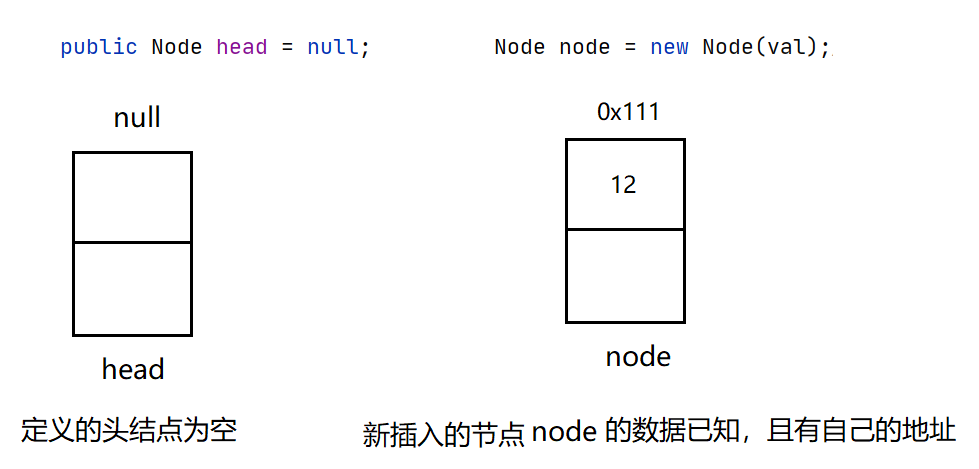
We have defined the header node in the class MyLinkedList. Therefore, in the process of header interpolation, we can draw a picture as follows:
Step 1: define that the head node is empty, and the inserted node defines a new data.
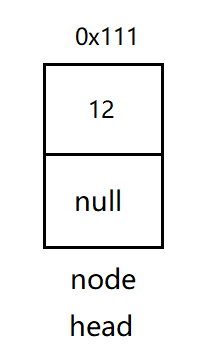
Step 2: let the next of the inserted node point to the head node, and then the head is equal to node, then the first data newly inserted is the head node of the new linked list.
Step 3: continue to insert new data
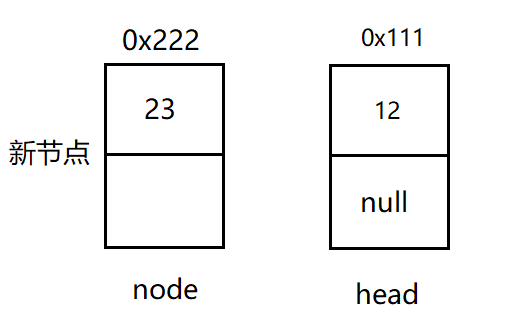
Repeat the step in step 2 to make the next of the inserted node equal to the address of the head node. In this way, the two nodes are connected together because of this address. The node points to the head from the node, and the head is equal to the address of the newly inserted node. Then the newly inserted node is the head node of the new linked list.
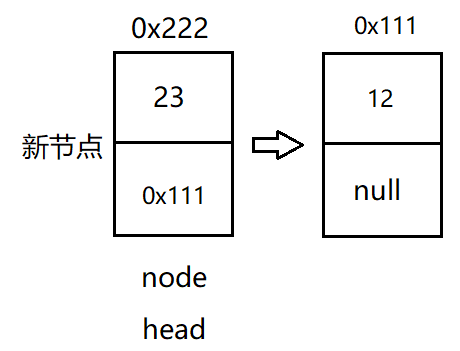
After that, the new node inserted can complete the head insertion method by repeating the step in step 2.
Interface 3: tail insertion method
Tail insertion method is to insert nodes from the tail node of the linked list, and each newly inserted node is the tail node of the new linked list.
//● tail interpolation
public void addLast(int val) {
Node node = new Node(val);
if(this.head == null) {//When there is no node
this.head = node;
}else {
Node cur = this.head;
while (cur.next != null) {
cur = cur.next;
}
//Cycle here, cur next == null;
cur.next = node;
}
}
Firstly, we consider the tail interpolation method with multiple nodes.
- First define a cur to traverse the linked list instead of head When next = null, the corresponding cycle ends;
- Then let's go to cur at the current tail node Next = address of the node to be inserted.
- The special case is: if the linked list is empty, you can directly make the node node equal to the head node.
Interface 4: plug in at any position
public Node searchIndexSubOne(int index) {//The specified index was found
Node cur = this.head;
/*while(index-1 != 0) {
cur = cur.next;
index--;
}*/
int count = 0;
while (count != index - 1) {//Determines whether the number of moves is equal to the specified subscript minus one
cur = cur.next;
count++;
}
return cur;//Moved to the designated position
}
//● insert at any position, and the first data node is subscript 0
public void addIndex(int index,int data) {
if(index < 0 || index > getLength()) {
System.out.println("Illegal location!!");
return;
}
if(index == 0) {
addFirst(data);
return;
}
if(index == getLength()) {
addLast(data);
return;
}
Node ret = searchIndexSubOne(index);
//ret stores the address (Reference) of the node at index-1
Node node = new Node(data);//Set inserted data
node.next = ret.next;//The address of the inserted data is equal to the address moved to the specified location
ret.next = node;//The address of ret moved to the specified location is equal to the reference of node
}
public int getLength() {
int len = 0;
Node cur = this.head;
while (cur != null) {
len++;
cur = cur.next;
}
return len;
}
General idea: insert at any position:
- Insert at the head node, which is equivalent to the head insertion method;
- Inserting at the tail node is equivalent to tail interpolation;
- Insert at a given position, find the inserted node according to a certain method, and then insert it.
Now let's discuss the third case:
To insert at any position, we have to find this position. From the figure, we can infer that assuming that the inserted position is the position with index 2, we only need to move cur to the previous node at position 2 to ensure that the new nodes can be connected. Then the relationship between cur and index is cur = index -1. We can use the loop, Calculate the number of times cur is moved, and then find the index. In this case, the insertion can be simply completed.
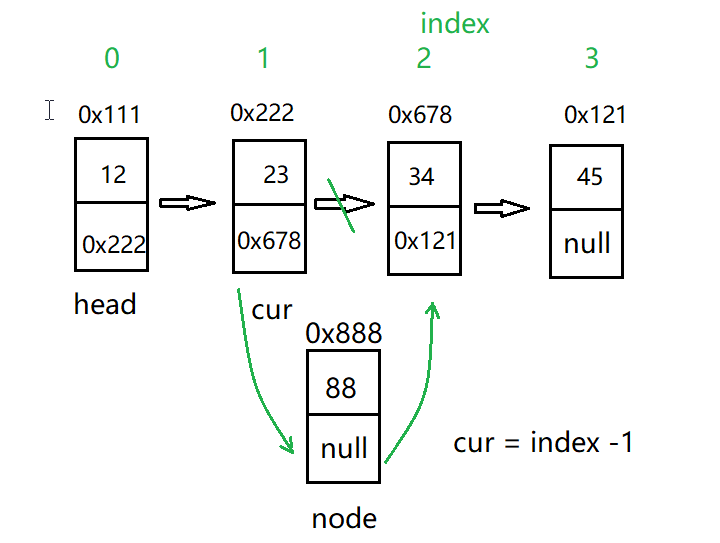
Interface 5: check whether there is a keyword in the linked list
//● check whether the keyword is included and whether the key is in the single linked list
public boolean contains(int key) {
Node cur = this.head;//Define a cur equal header through the Node
while(cur != null) {
if(cur.val == key) {
return true;
}
cur = cur.next;
}
return false;
}
The above interface is implemented. The implementation of this interface is very simple. You only need to traverse the linked list once to determine whether the keyword is in the linked list.
Interface 6: delete the node whose keyword is key for the first time
General idea: the node to be deleted is not the head node or tail node
As shown in the figure below, assuming that we want to delete the third node, we only need to find the precursor node of the node to be deleted and directly let cur The value of next is equal to the address of the last node.
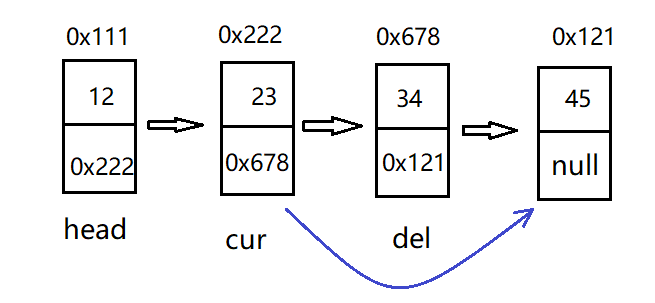
But how to find the node to be deleted and its precursor node cur only after traversing the linked list once? At this point, you need to write a method to find the precursor node. The following code is easy to understand.
//Find the precursor of key from the beginning
public Node searchPrev(int key) {
Node cur = this.head;
while(cur.next != null){
if(cur.next.val == key) {//Judge that the next value of the current node is not equal to key
return cur;//If equal to, this node is the precursor
}
cur = cur.next;
}
//When the cycle is finished, it means that it is not found
return null;
}
//● delete the node whose keyword is key for the first time
public void remove(int key){
//1. Judge whether the header node is the node to be deleted
if(this.head.val == key) {//When the keyword is equal to head
this.head = this.head.next;//Just make the head node equal to head Value of next
return;
}
//2. Find the precursor node of the key. The reason for finding the precursor node: if the deleted node is in the middle of the linked list and the deleted node is gone, the reference of the precursor node must be changed to the node of the deleted data, so that the linked list is complete
Node prev = searchPrev(key);
if(prev == null) {
System.out.println("There is no node to delete!");
return;
}
//The specified deletion location was found
Node del = prev.next;//del is a node
//Start deletion
prev.next =del.next;
}
Overall idea:
- First judge whether the end node is the node to be deleted;
- Then find the precursor node;
- Next, find the node to delete;
- Finally, you can delete it directly.
Interface 7: delete all nodes with key value
Idea: to delete a node, you have to find the precursor node of the node. Consider the case where multiple values need to be deleted, and also consider the case where the header node is to be deleted. cur is equivalent to the node to be deleted.
//Delete all nodes with the value of key
public void removeAllKey(int key) {
Node cur = this.head.next;
Node prev = this.head;
//Each element of the single linked list should be traversed
while (cur != null) {
if (cur.val == key) {
//This is the node you want to delete
prev.next = cur.next;
cur = cur.next;
}else {
prev = cur;//Or prev = prev next;
cur = cur.next;
}
}
if(this.head.val == key) {
this.head =this.head.next;
}
}
Interface 8: clear single linked list
Idea: you can directly make the head node null, or write a loop to make each node empty in the process of traversing the linked list. We also have to consider the case of only one node.
public void clear() {
//this.head = null;
Node cur = this.head;
while (cur != null) {
Node curNext = cur.next;
cur.next = null;
cur = curNext;
}
this.head = null;//Finally, the header node should be recycled
}
3.2. 2 implementation of headless bidirectional linked list
Headless two-way linked list is similar to single linked list. It is connected by nodes, but each node has three fields: the first field represents the number of the current node, the second field represents the address of the predecessor node of the current node, and the third field represents the address of the next node. As shown in the figure below, it points to a simple headless two-way linked list.
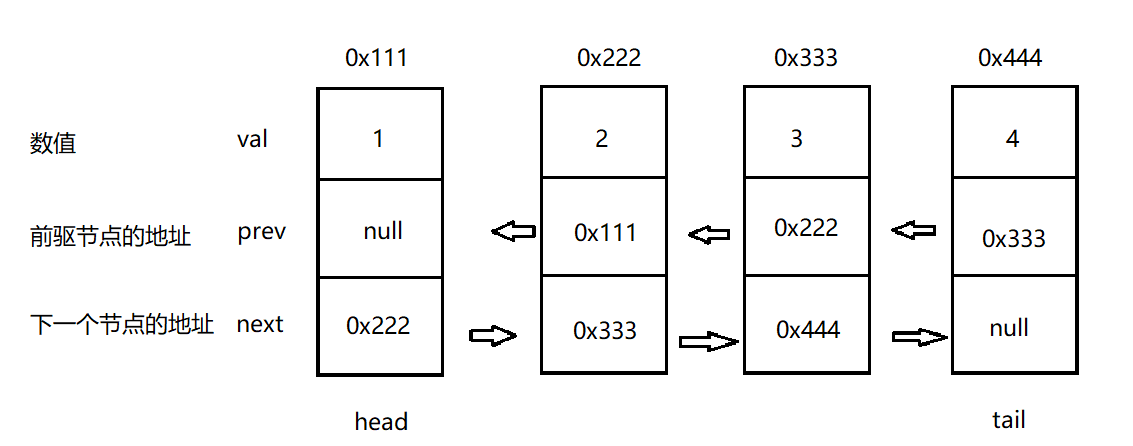
To implement a headless two-way linked list, similar to a single linked list, create a ListNode class, define the data, the address of the precursor node and the address of the next node in this class, and then assign values to the nodes of the class by the construction method:
class ListNode {
public int val;
public ListNode prev;
public ListNode next;
public ListNode(int val) {
this.val = val;//point
}
}
Interface 1: print function
Next, create a MyDoubleList class to represent the headless bidirectional linked list. All interfaces of the headless bidirectional linked list will be implemented in this class
public class MyDoubleList {
public ListNode head;//head
public ListNode tail;//tail
//Printing method
public void display() {
ListNode cur = this.head;
while (cur != null) {
System.out.print(cur.val + " ");
cur = cur.next;
}
System.out.println();
}
}
Interface 2: head insertion method
//Head insertion
public void addFirst(int data) {
ListNode node = new ListNode(data);
if (this.head == null) {//First insertion
this.head = node;
this.tail = node;
}else {
node.next = this.head;
this.head.prev = node;
this.head = node;
}
}
Interface 3: tail insertion method
//Tail interpolation
public void addLast(int data) {
ListNode node = new ListNode(data);
if (head == null) {//First insertion
this.head = node;
this.tail = node;
}else {
this.tail.next = node;
node.prev = this.tail;
this.tail = this.tail.next;
}
}
Interface 4: plug in at any position
//Find the subscript where the node is located
public ListNode findIndex(int index) {
ListNode cur = this.head;
int count = 0;
while (count != index) {
cur = cur.next;
count++;
}
return cur;
}
//Insert at any position, and the first data node is subscript 0
public void addIndex(int index,int data) {
if (index <0 || index >size()) {
System.out.println("index wrongful!!");
return;
}
if (index == 0) {
addFirst(data);
return;
}
if (index == this.size()) {
addLast(data);
return;
}
ListNode cur = findIndex(index);
ListNode node = new ListNode(data);
node.next = cur;
cur.prev.next = node;
node.prev = cur.prev;
cur.prev = node;
}
Interface 5: check whether the keyword key is in the linked list
//Find out whether the keyword is included and whether the key is in the linked list
public boolean contains(int key) {
ListNode cur = this.head;
while (cur != null) {
if (cur.val == key) {
return true;
}
cur = cur.next;
}
return false;
}
Interface 6: delete the node whose keyword is key for the first time
//Delete the node whose keyword is key for the first time
public void remove(int key) {
ListNode cur = this.head;
while (cur != null) {
if (cur.val == key) {
if (this.head.val == key) {//The deleted node is the head node
this.head = this.head.next;
if (this.head != null) {//The linked list has only one node and needs to be deleted
this.head.prev = null;
}else {
this.tail = null;
}
}else {//Middle and tail nodes
if (cur.next != null) {//middle
cur.prev.next = cur.next;
cur.next.prev = cur.prev;
}else {//Tail node
cur.prev.next = cur.next;
tail = cur.prev;
}
}
return;
}else {
cur = cur.next;
}
}
}
Interface 7: delete all nodes with key value
//Delete all nodes with the value of key
public void removeAllKey(int key) {
ListNode cur = this.head;
while (cur != null) {
if (cur.val == key) {
if (this.head.val == key) {//The deleted node is the head node
this.head = this.head.next;
if (this.head != null) {//The linked list has only one node and needs to be deleted
this.head.prev = null;
}else {
this.tail = null;
}
}else {//Middle and tail nodes
if (cur.next != null) {//middle
cur.prev.next = cur.next;
cur.next.prev = cur.prev;
}else {//Tail node
cur.prev.next = cur.next;
tail = cur.prev;
}
}
}
cur = cur.next;
}
}
Interface 8: get the length of the linked list
//Get the length of the linked list
public int size() {
int count = 0;
ListNode cur = this.head;
while (cur != null) {
cur = cur.next;
count++;
}
return count;
}
Interface 9: empty linked list
public void clear() {
ListNode cur = this.head;
while (cur != null) {
ListNode curNext = cur.next;
cur.next = null;
cur.prev = null;
cur = curNext;
}
this.head = null;
this.tail = null;
}
3.3 chain surface test questions
1. Delete all nodes in the linked list equal to the given value val
Force buckle topic: Remove linked list elements.
The code of this problem is the same as the code of interface 7 mentioned above, but it needs to be judged when the force buckle is applied:
if (head == null) return null;//If there is no node in the linked list, null will be returned and nothing can be deleted
Then return a head at the end of the code to run.
2. Reverse single linked list
Force buckle topic: Reverse a single linked list.
Reversing the linked list means that the node is reversed, that is, the node points backwards. As shown below:
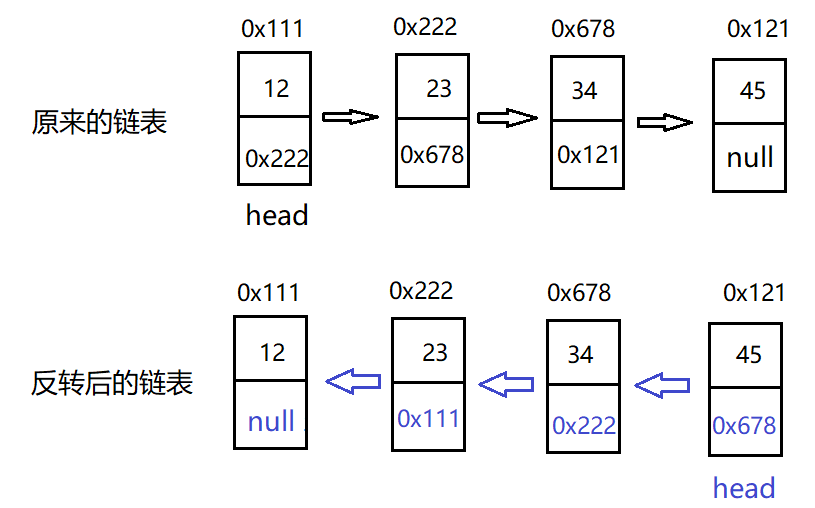
Idea 1: use the head insertion method to check the nodes behind the original linked list to the front of the head node.
/**
* Give you the head node of the single linked list. Please reverse the linked list and return the reversed linked list.
* Using head insertion method
* @return
*/
public Node reverseList() {
if (head == null ||this.head.next == null) {
return this.head;
}
//cur represents a node that is currently to be flipped or headlined
Node cur = this.head;
Node curNext = cur.next;
//Processing header node
cur.next = null;
cur = curNext;
while(cur != null) {//Head insertion
curNext = cur.next;
cur.next = this.head;
this.head = cur;
cur = curNext;
}
return this.head;
}
/**
Idea 2: define a precursor node with the following code:
/**
* Give you the head node of the single linked list. Please reverse the linked list and return the reversed linked list.
* New method: define a precursor node
* @return
*/
public Node reverseList1() {
Node prev = null;
Node cur = this.head;
Node newHead = null;
while (cur != null) {
Node curNext = cur.next;
if (curNext == null) {
newHead = cur;
}
cur.next = prev;
prev = cur;
cur = curNext;
}
return newHead;
}
Since a new header node is defined when the reverseList1() class is written, a new show2 method needs to be called when checking:
//Start printing according to the specified node position (this printing function is used in conjunction with the method reverseList1())
public void show2(Node newHead) {
Node cur = newHead;
while (cur != null) {
System.out.print(cur.val + " ");
cur = cur.next;
}
}
3. Return the intermediate node of the linked list
Force buckle topic: Returns the intermediate node of the linked list.
Title Description: given a non empty single linked list with head node, return the intermediate node of the linked list. If there are two intermediate nodes, the second intermediate node is returned.
Idea: the speed node defines a fast, two steps at a time, and defines a slow node, one step at a time, when fast or fast When next is null, the position of slow is the position of the intermediate node. This idea is applicable to odd and even nodes.
/**
* Given a non empty single linked list with head node, return the intermediate node of the linked list. If there are two intermediate nodes, the second intermediate node is returned
* @return
*/
public Node middleNode() {
Node fast = this.head;
Node slow = this.head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
}
return slow;
}
4. Input a linked list and output the penultimate node in the linked list
Niuke topic: Input a linked list and output the penultimate node in the linked list..
Idea: to output the penultimate node, you need to define two nodes, fast and slow. Fast takes the k-1 step first, and then slow and fast go together when fast or fast When next is null, the position of slow is the penultimate node.
Note: judge the rationality of k value; Judge the condition of empty linked list
/**
* Input a linked list and output the penultimate node in the linked list.
* @param k
* @return
*/
public Node findKthToTail(int k) {
if(k <= 0 || head == null) {
return null;
}
Node fast = this.head;
Node slow = this.head;
while (k-1 != 0) {
if (fast.next != null) {
fast = fast.next;
k--;
}else {
System.out.println("Given k The value is too big!!");
return null;
}
}
//Here, fast took k-1 steps
while(fast.next != null) {
fast = fast.next;
slow = slow.next;
}
return slow;
}
5. Linked list segmentation
Niuke topic: Linked list segmentation.
Title Description: write code to divide the linked list into two parts based on the given value x. all nodes less than x are arranged before nodes greater than or equal to x.
Idea: as shown in the figure below. A single linked list with 5 nodes. Assuming a given x = 30, we can insert the number smaller than 30 into the front line segment, insert the number larger than 30 into the rear line segment, and finally connect the two line segments into a linked list.
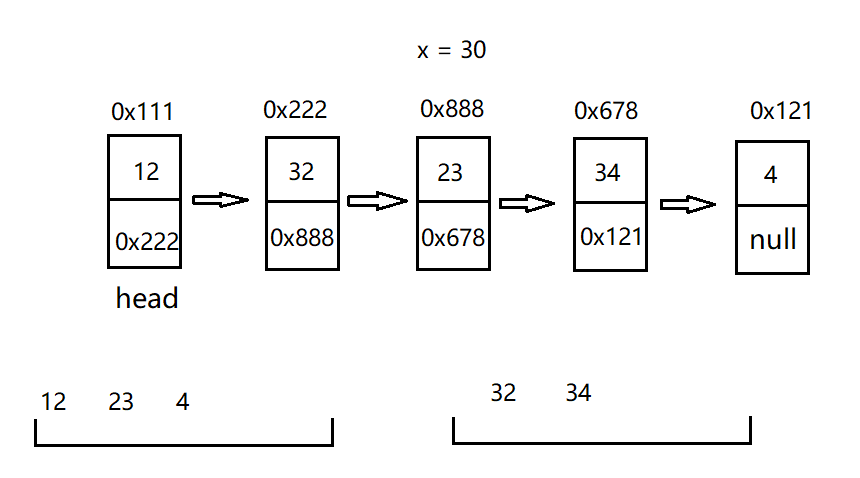Note: after thinking according to the above ideas, we need to pay attention to some special situations.
- 1. First consider the first insertion and not the first insertion of the two parts;
- 2. All data are smaller than the specified data, that is, all data are inserted into the first half, and the second half is empty, and vice versa;
- 3. There is just one node in the second half. You need to set the next value of the node to null, otherwise it will cause an endless loop.
/**
* Write code to divide the linked list into two parts based on the given value X. all nodes less than X are arranged before nodes greater than or equal to x, and the original data order cannot be changed. Return the head pointer of the rearranged linked list
* @param x
* @return
*/
public Node partition(int x) {
Node cur = this.head;
Node bs = null;//bs is the abbreviation of before start
Node be = null;//bs is the abbreviation of before end
Node as = null;//afterstart
Node ae = null;
while (cur != null) {
if (cur.val < x) {//Less than x
if(bs == null) {//First insertion of less than part
bs = cur;
be = cur;
}else {
be.next = cur;
be = be.next;
}
}else {//Greater than or equal to x
if (as == null) {//First insertion of greater than part
as = cur;
ae = cur;
}else {
ae.next = cur;
ae = ae.next;
}
}
cur = cur.next;
}
if (bs == null) {//Here, judge if the value of x is smaller than all the numbers in the linked list
return as;//Returns the head linked list of the second half
}
be.next = as;//After traversing the linked list, connect the two separate parts
if (as != null) {//The last data is less than x and is placed in the first half. If there is no tail node in the whole linked list, it will enter an endless loop.
ae.next = null;//ae and as were together at the beginning, and ae moved behind
}
return bs;
}
6. Delete duplicate nodes in the linked list
Niuke topic: Delete duplicate nodes in the linked list.
Title Description: in a sorted linked list, there are duplicate nodes. Please delete the duplicate nodes in the linked list. The duplicate nodes are not retained and the chain header pointer is returned.
Idea: define a cur and let it traverse the linked list; Define a puppet node tmphead. First judge cur next != null && cur. val == cur.next. Val this condition, and then let tmpahead next = cur； tmpHead = tmpHead.next； Cur continues to traverse backwards. When encountering repeated numbers, write a loop and let cur continue to traverse backward. At the end of the loop, cur is at the last of the same number, and then jump out of the loop and let cur traverse a node later to make cur The value of next is equal to the tmpahead node, so the linked list is connected.
be careful:
- 1. Judge whether the linked list is empty;
- 2. Except for the head node, the numbers of other nodes are the same, so you need to pay attention to setting the next value of the head node to null.
/**
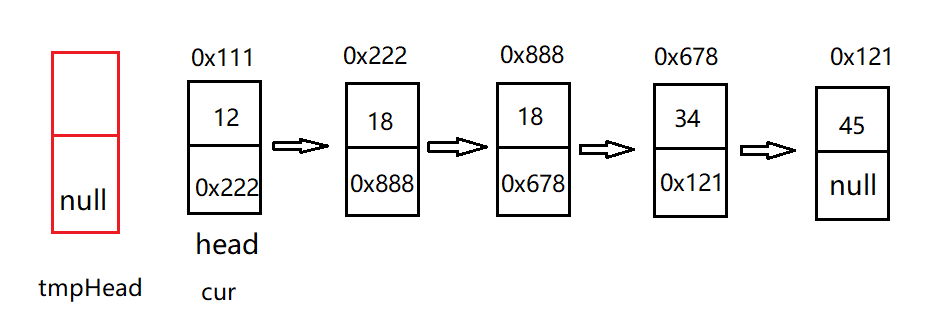
* In a sorted linked list, there are duplicate nodes. Please delete the duplicate nodes in the linked list. The duplicate nodes are not retained and the chain header pointer is returned. For example, the linked list 1 - > 2 - > 3 - > 3 - > 4 - > 4 - > 5 is 1 - > 2 - > 5 after processing
* @return
*/
public Node deleteDuplication() {
Node cur = this.head;
Node tmpHead = new Node(-1);//Define a puppet node to ensure that one node is fixed.
Node newHead = tmpHead;//This considers that the linked list is the same from the beginning node, and only the tail node is different
while (cur != null) {
if (cur.next != null && cur.val == cur.next.val) {//Duplicate nodes found
while (cur.next != null && cur.val == cur.next.val) {
cur = cur.next;
}
cur = cur.next;
}else {//No duplicate nodes found
tmpHead.next = cur;
tmpHead = tmpHead.next;
cur = cur.next;
}
}
tmpHead.next = null;//Prevent only one header node after deletion
return newHead.next;
}
This problem is a little more difficult and needs more practice
7. Palindrome structure
Niuke topic: Palindrome structure of linked list.
Title Description: for a linked list, please design an algorithm with time complexity of O(n) and additional space complexity of O(1) to judge whether it is palindrome structure.
Idea:
- First, use the speed node to find the intermediate node of the current linked list;
- Then reverse the second half of the linked list;
- When reversing, start from the next node of slow (the same applies to even nodes).
Note: consider the case of odd and even nodes
/**
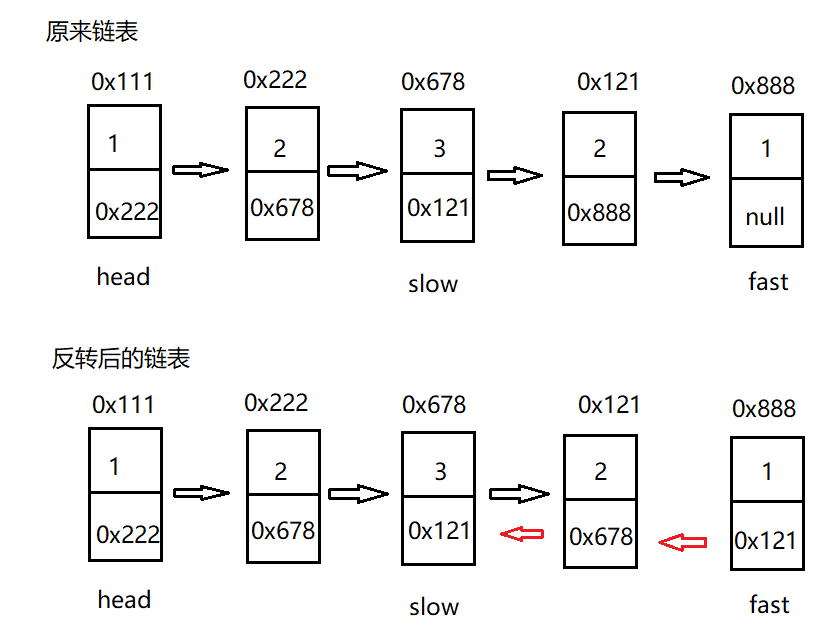
*For a linked list, please design an algorithm with time complexity of O(n) and additional space complexity of O(1) to judge whether it is palindrome structure,
*Given the header pointer A of A linked list, please return A bool value to represent whether it is A palindrome structure. Ensure that the length of the linked list is less than or equal to 900.
* Test example: 1 - > 2 - > 2 - > 1
* Return: true
* @return
*/
public boolean chkPalindrome() {
if (this.head == null) return false;//The header node is empty
if (this.head.next == null) return true;//Only one node
Node fast = this.head;
Node slow = this.head;
while (fast != null && fast.next != null) {//Find the intermediate node with slow
fast = fast.next.next;
slow = slow.next;
}
Node cur = slow.next;
while (cur != null) {//Flip the second half of the linked list
Node curNext = cur.next;
cur.next = slow;
slow = cur;
cur = curNext;
}
while (this.head != slow) {
if (this.head.val != slow.val) {
return false;
}
if (this.head.next == slow) {//When the number of nodes is even
return true;
}
this.head = this.head.next;
slow = slow.next;
}
return true;
}
8. Judge whether there are links in the linked list
Force buckle topic: Given a linked list, judge whether there are links in the linked list.
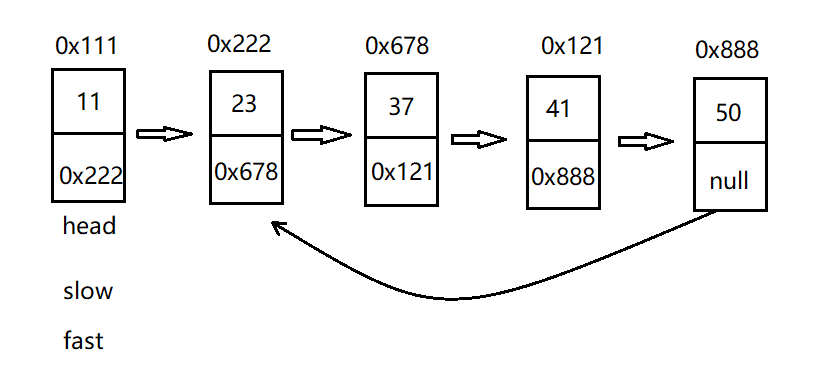
Idea: as shown below. Define the speed node, a fast node and a slow node. Fast takes two steps at a time and slow takes one step at a time. When fast and slow meet again, it shows that the linked list has rings.
Q: why can't fast take only two steps, three or four steps?
A: two steps can ensure the fastest meeting. Three or four steps may be missed several times before meeting.
/**
* Given a linked list, judge whether there are links in the linked list.
* @return
*/
public boolean hasCycle() {
Node fast = this.head;
Node slow = this.head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) {
return true;
}
}
return false;
}
9. Return the first node of the linked list into the ring
Force buckle topic: Returns the first node of the linked list into the ring.
Title Description: given a linked list, return the first node from the linked list into the ring. If the linked list is acyclic, null is returned.
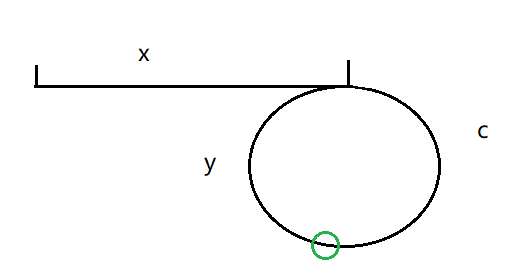
Idea: set two nodes, fast and slow. Fast takes two steps at a time and slow takes one step at a time.
Suppose in the linked list, as shown in the following figure, x is the number of nodes traversed before entering the ring, c is the length of the ring, the green part is the point met on the ring, and its distance from the node entering the ring is y. Since the speed of fast is twice that of slow, there is a double relationship between the distance when we meet.
When meeting:
- Slow node slow: x+c-y
- fast node: x+c+c-y
From the above relationship, we can deduce that x=y
/**
* Given a linked list, return the first node from the linked list into the ring. If the linked list is acyclic, null is returned
* @return
*/
public Node detectCycle() {
Node fast = this.head;
Node slow = this.head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) {
break;
}
}
if (fast == null || fast.next == null) {
return null;
}
slow = this.head;
while (fast != slow) {
slow = slow.next;
fast = fast.next;
}
return slow;
}
10. Two linked lists: merge two ordered linked lists
Force buckle topic: Merge two ordered linked lists.
Title Description: merge two ascending linked lists into a new ascending linked list and return. The new linked list is composed of all nodes of a given two linked lists.
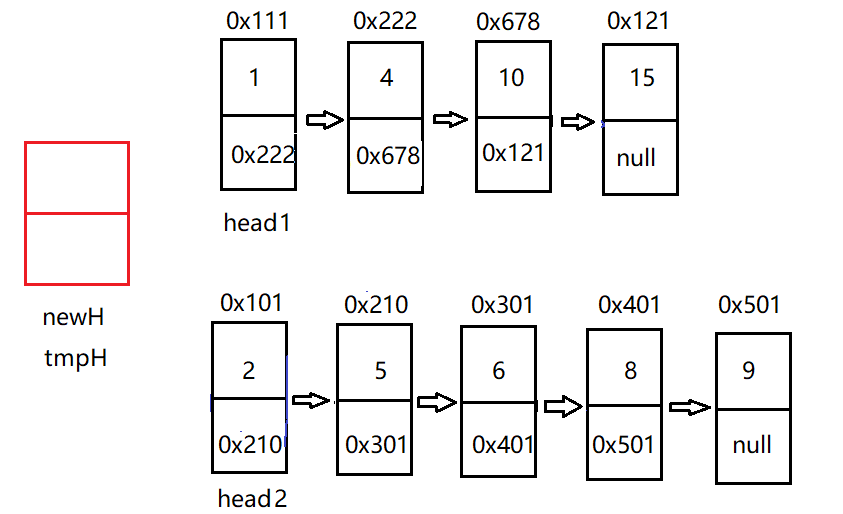
Idea: since we cannot determine which of the two nodes has a larger number of head nodes, we first define a puppet node newH, let tmpHead = newHead, and let tmpHead traverse the two linked lists instead of newHead. The following figure is an example:
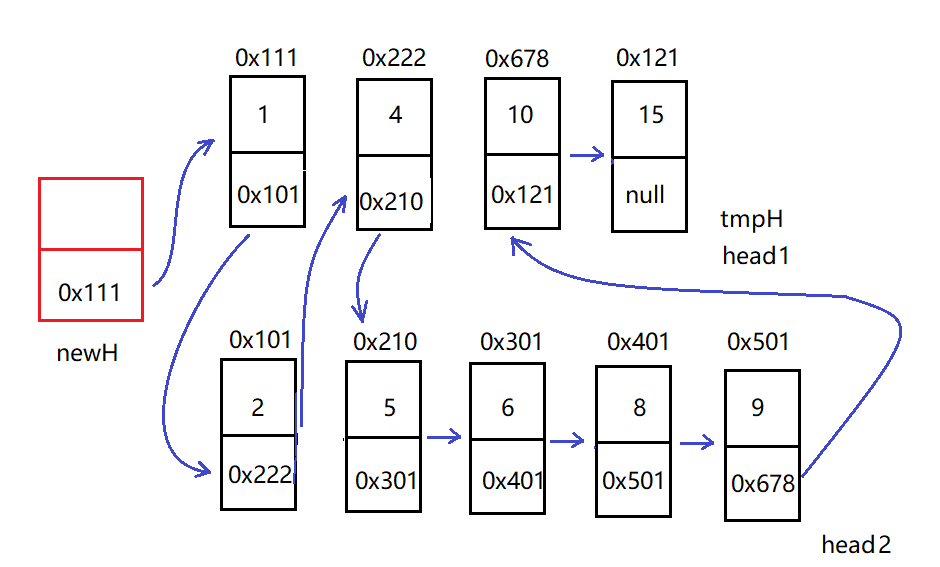
After defining the puppet node, it is judged that the value of head1 is small, then the puppet node points to the head node of head1, head1 = head1 next，tmpHead = tmpHead.next, and then compare the size of the second node of head1 and the head node of head2, and so on.
In the process of traversal, the two linked lists connect all nodes together according to the definition of single linked list, and the two linked lists are combined into an ordered single linked list. The steps in the figure above are as follows:
/**
* Merge the two ascending linked lists into a new ascending linked list and return. The new linked list is composed of all nodes of a given two linked lists.
* @param head1 Represents the header node of the first single linked list
* @param head2 Represents the header node of the first single linked list
* @return
*/
public static Node mergeTwoLists(Node head1, Node head2) {
Node newHead = new Node(-1);//Define a puppet node
Node tmpHead = newHead;
while (head1 != null && head2 != null) {
if (head1.val < head2.val) {
tmpHead.next = head1;//point
head1 = head1.next;
tmpHead = tmpHead.next;//Move back
}else {
tmpHead.next = head2;//point
head2 = head2.next;
tmpHead = tmpHead.next;
}
}
if (head1 != null) {//In this case, one linked list has been traversed and the other has not been traversed. It directly points to the linked list that has not been traversed.
tmpHead.next = head1;
}
if (head2 != null) {
tmpHead.next = head2;
}
return newHead.next;
}
public static void main(String[] args) {
MyLinkedList myLinkedList = new MyLinkedList();
myLinkedList.addLast(1);
myLinkedList.addLast(3);
myLinkedList.addLast(5);
myLinkedList.addLast(7);
myLinkedList.addLast(10);
myLinkedList.show();
MyLinkedList myLinkedList2 = new MyLinkedList();
myLinkedList2.addLast(2);
myLinkedList2.addLast(4);
myLinkedList2.addLast(6);
myLinkedList2.addLast(8);
myLinkedList2.addLast(13);
myLinkedList2.show();
Node ret = mergeTwoLists(myLinkedList.head,myLinkedList2.head);
myLinkedList2.show2(ret);
}
11. Two linked lists: find the common nodes of the two linked lists
Find the common nodes of the two linked lists.
Title Description: enter two linked lists and find their first common node. If the two linked lists do not have intersecting nodes, null is returned.
Idea: when two linked lists intersect, the result must be Y-shaped.
The following figure shows the results of the intersection of two linked lists. At this time, the length of head 1 is 4 and the length of head 2 is 5. Our main idea is to let the longer linked list take the absolute value step of their difference first, and then the two linked lists go together. When the two nodes meet for the first time, the node is what we want.
/**
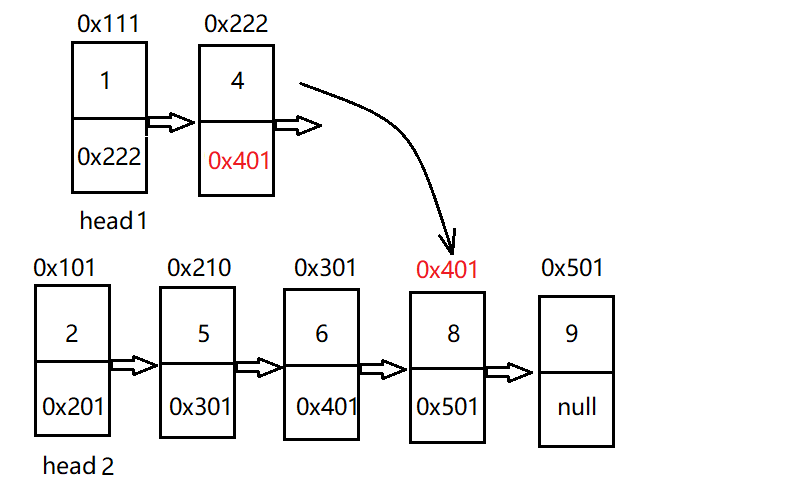
* Find the starting node where two single linked lists intersect
* @param headA
* @param headB
* @return
*/
public static Node getIntersectionNode(Node headA, Node headB) {
//0. Judge whether it is empty
if (headA == null || headB == null) return null;
//1. Calculate the length of the two linked lists respectively
int lenA = 0;
int lenB = 0;
Node pl = headA;//The default length of these two lines is headA and headB.
Node ps = headB;
while (pl != null) {
lenA++;
pl = pl.next;
}
while (ps != null) {
lenB++;
ps = ps.next;
}
pl = headA;//Be sure to rewrite it back
ps = headB;
int len = lenA - lenB;
if (len < 0) {
pl = headB;
ps = headA;
len = Math.abs(lenA-lenB);//The absolute value function is referenced here, which is equivalent to len = headb heada to ensure that len is a positive number
}
//pl must be a long list and ps must be a short list
while (len != 0) {//The difference of the first go length of the long linked list
pl = pl.next;
len--;
}//So far, the two linked lists are on the same starting line
while (pl != ps) {//Next, the two linked lists start walking synchronously
pl = pl.next;
ps = ps.next;
}
if (pl == null || ps == null) {
return null;
}
return pl;
}
/**
* Find the starting node where two single linked lists intersect
* @param args
*/
public static void main17(String[] args) {
MyLinkedList myLinkedList = new MyLinkedList();
myLinkedList.addLast(1);
myLinkedList.addLast(5);
myLinkedList.addLast(7);
myLinkedList.show();
MyLinkedList myLinkedList2 = new MyLinkedList();
myLinkedList2.addLast(2);
myLinkedList2.addLast(3);
myLinkedList2.addLast(4);
myLinkedList2.addLast(6);
myLinkedList2.addLast(7);
myLinkedList2.addLast(8);
myLinkedList2.addLast(13);
myLinkedList2.show();
Node ret = getIntersectionNode(myLinkedList.head, myLinkedList2.head);
creatCut(myLinkedList.head,myLinkedList2.head);
System.out.println(getIntersectionNode(myLinkedList.head,myLinkedList2.head).val);
}
12. Other linked list topics
Niuke.com: Linked list title.
Force buckle: Linked list title.
summary
The content of the linked list is very complex. You need to practice and draw more pictures. If you encounter a problem, first draw the structure of the linked list, then analyze and write the general code. If the general situation can pass, you have to consider more special positions and improve the code step by step. If you don't have rich exercise, you want to write a complete code of the linked list at one time, It is almost impossible, so we must practice and draw more pictures; Practice more and draw more pictures; Practice and draw more!!!