1. Problem Description:
In 1944, special forces Mike received an order from the Ministry of defense to rush to an isolated island in the Pacific Ocean to rescue Private Ryan captured by the enemy. Ryan was imprisoned in a maze with complex terrain, but fortunately Mike got the topographic map of the maze. The shape of the maze is a rectangle. Its north-south direction is divided into N rows and east-west direction is divided into m columns, so the whole maze is divided into N rows × M units. The position of each cell can be represented by an ordinal number pair (cell row number, cell column number). The two adjacent units in the North-South or east-west direction may be interconnected, there may be a locked door, or an insurmountable wall. Note: the door can pass through in two directions, that is, it can be regarded as an undirected edge. Some units in the maze store keys. The same unit may store multiple keys, and all doors are divided into P categories. The keys to open the same doors are the same, and the keys of different doors are different. Private Ryan was held in the southeast corner of the maze, unit (N,M), and was unconscious. The maze has only one entrance, in the northwest corner. That is, the microphone can directly enter the (1,1) unit. In addition, the time for the microphone to move from one unit to another adjacent unit is 1, and the time for taking the key of the unit and opening the door with the key can be ignored. Try to design an algorithm to help Mike reach Ryan's unit in the fastest way and rescue Private Ryan.
Input format
The first line has three integers representing the values of N, m and P. The second line is an integer k, which represents the total number of doors and walls in the maze. Next K lines, each line contains five integers, Xi1,Yi1,Xi2,Yi2,Gi: when Gi ≥ 1, there is a Gi class door between (Xi1,Yi1) and (Xi2,Yi2) units; when Gi=0, there is an insurmountable wall between (Xi1,Yi1) and (Xi2,Yi2) units. The next line contains an integer S, which represents the total number of keys stored in the maze.
Next, in line S, each line contains three integers Xi1, Yi1 and Qi, indicating that there is a key that can open the Qi door in the (Xi1,Yi1) unit.
Output format
Output the shortest time for Mike to rescue Private Ryan. If the problem has no solution, output - 1.
Data range
|Xi1−Xi2| + |Yi1−Yi2| = 1,
0 ≤ Gi ≤ P,
1 ≤ Qi ≤ P,
1 ≤ N,M,P ≤ 10,
1 ≤ k ≤ 150
Input example:
4 4 9
9
1 2 1 3 2
1 2 2 2 0
2 1 2 2 0
2 1 3 1 0
2 3 3 3 0
2 4 3 4 1
3 2 3 3 0
3 3 4 3 0
4 3 4 4 0
2
2 1 2
4 2 1
Output example:
14
Example explanation:
The maze is as follows:
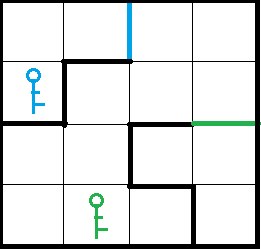
Source: https://www.acwing.com/problem/content/description/1133/
2. Train of thought analysis:
3. The code is as follows:
python:
from typing import List
import heapq
class Solution:
# It is also possible to use dijkstra plain version to solve the shortest path, or use double ended queue wide search (the weight is only 0 and 1)
def dijkstra(self, n: int, m: int, key: List[int], g: List[List[int]]):
INF = 10 ** 10
# p is the maximum number of key types, and the corresponding maximum binary state is 1 < < 10
p = 10
# The first dimension represents the current position (one-dimensional coordinate is equivalent to two-dimensional coordinate), and the second dimension represents the key state
dis = [[INF] * (1 << p) for i in range((n * m + 10))]
# vis needs two dimensions, which is the same as dis
vis = [[0] * (1 << p) for i in range((n * m + 10))]
dis[1][0] = 0
q = list()
# The first element of the tuple must have the current shortest distance, the second element is the current one-dimensional coordinate position (which can be regarded as two-dimensional coordinates), and the third element is the current key state
heapq.heappush(q, (0, 1, 0))
while q:
# x indicates the current position and y indicates the current key status
d, x, y = heapq.heappop(q)
# The current state is in the heap
if vis[x][y]: continue
vis[x][y] = 1
# Take the key directly when you have it, because it doesn't cost you any time
if key[x]:
# Update key status,
state = y | key[x]
# Update the current 2D status
if dis[x][state] > dis[x][y]:
dis[x][state] = dis[x][y]
# If there are updates, they need to be added to the heap
heapq.heappush(q, (dis[x][state], x, state))
# Traverse the adjacent nodes (previously, walking edges were built in the upper, lower, left and right directions)
for next in g[x]:
# There's a door, but there's no key
if next[1] > 0 and y >> (next[1] - 1) & 1 == 0: continue
# Update reachable status
if dis[next[0]][y] > dis[x][y] + 1:
dis[next[0]][y] = dis[x][y] + 1
# If there are updates, they need to be added to the heap
heapq.heappush(q, (dis[next[0]][y], next[0], y))
# Enumerate the answers. The second indicates the state of the key. Enumerating n * m is equivalent to the last position of the two-dimensional coordinates (the two-dimensional coordinates and one-dimensional coordinates are mapped one by one)
res = INF
for i in range(1 << p):
res = min(res, dis[n * m][i])
# Note that - 1 needs to be returned when there is no solution to the problem
return res if res != INF else -1
# Here, you can create a position that can be reached directly up, down, left and right at the current position
def build(self, n: int, m: int, mp: List[List[int]], g: List[List[int]], dic: dict):
pos = [[0, 1], [0, -1], [-1, 0], [1, 0]]
for i in range(1, n + 1):
for j in range(1, m + 1):
for u in range(4):
x, y = i + pos[u][0], j + pos[u][1]
if 0 < x <= n and 0 < y <= m:
# Judge whether it already exists in the dictionary. If it does not exist, the description can be passed directly. Create an edge with an edge weight of 0
a, b = mp[i][j], mp[x][y]
if (a, b) not in dic:
# There is no need to create it twice, because each point will start by itself, so two-way edges will be created in the end
# Creating an edge with an edge weight of 0 means that the time spent is 0
g[a].append((b, 0))
def process(self):
# n * m line, p is the total number of key types (not used after p)
n, m, p = map(int, input().split())
# The mp list is the mapping of two-dimensional coordinates to one-dimensional coordinates
mp = [[0] * (m + 1) for i in range(n + 1)]
t = 1
for i in range(1, n + 1):
for j in range(1, m + 1):
mp[i][j] = t
t += 1
k = int(input())
# Because two-dimensional coordinates are mapped to one-dimensional coordinates, it is necessary to declare at least the number of nodes of n * m + 1. From two-dimensional coordinates to one-dimensional coordinates can save some space and be expressed conveniently
g = [list() for i in range(n * m + 10)]
dic = dict()
for i in range(k):
# There is a door or wall between (x1, Y2) and (X2, Y2). When C > = 1, it indicates the door
x1, y1, x2, y2, c = map(int, input().split())
# Use a hash table to record whether there are walls or doors between them
a, b = mp[x1][y1], mp[x2][y2]
# Mark that the current coordinates have been accessed, so that you can distinguish whether there is a wall or a door or nothing in the adjacent position that can be passed directly. When there is a door or a wall, the last thing left in the mark in the dic is the situation that can be passed directly
dic[(a, b)] = 1
dic[(b, a)] = 1
# c greater than 0 indicates that an edge needs to be built
if c:
g[a].append((b, c))
g[b].append((a, c))
# Use loops to create edges that go directly from one location to another (note that)
self.build(n, m, mp, g, dic)
# Learn the position of the key and the corresponding key type·
s = int(input())
key = [0] * (n * m + 1)
for i in range(s):
x, y, q = map(int, input().split())
# Key [] is a decimal number that can be regarded as a binary number. If the current key type is q, it is marked as 1 on the corresponding binary bit. Because there may be multiple keys in the same position, it needs to be used or calculated. 1 < < q - 1 is equivalent to: 1 < < (q - 1)
key[mp[x][y]] |= 1 << q - 1
return self.dijkstra(n, m, key, g)
if __name__ == "__main__":
print(Solution().process())c++:
#include <cstring>
#include <iostream>
#include <algorithm>
#include <deque>
#include <set>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
const int N = 11, M = 360, P = 1 << 10;
int n, m, k, p;
int h[N * N], e[M], w[M], ne[M], idx;
int g[N][N], key[N * N];
int dist[N * N][P];
bool st[N * N][P];
set<PII> edges;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void build()
{
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
for (int u = 0; u < 4; u ++ )
{
int x = i + dx[u], y = j + dy[u];
if (!x || x > n || !y || y > m) continue;
int a = g[i][j], b = g[x][y];
if (!edges.count({a, b})) add(a, b, 0);
}
}
int bfs()
{
memset(dist, 0x3f, sizeof dist);
dist[1][0] = 0;
deque<PII> q;
q.push_back({1, 0});
while (q.size())
{
PII t = q.front();
q.pop_front();
if (st[t.x][t.y]) continue;
st[t.x][t.y] = true;
if (t.x == n * m) return dist[t.x][t.y];
if (key[t.x])
{
int state = t.y | key[t.x];
if (dist[t.x][state] > dist[t.x][t.y])
{
dist[t.x][state] = dist[t.x][t.y];
q.push_front({t.x, state});
}
}
for (int i = h[t.x]; ~i; i = ne[i])
{
int j = e[i];
if (w[i] && !(t.y >> w[i] - 1 & 1)) continue; // There are doors and no keys
if (dist[j][t.y] > dist[t.x][t.y] + 1)
{
dist[j][t.y] = dist[t.x][t.y] + 1;
q.push_back({j, t.y});
}
}
}
return -1;
}
int main()
{
cin >> n >> m >> p >> k;
for (int i = 1, t = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
g[i][j] = t ++ ;
memset(h, -1, sizeof h);
while (k -- )
{
int x1, y1, x2, y2, c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
int a = g[x1][y1], b = g[x2][y2];
edges.insert({a, b}), edges.insert({b, a});
if (c) add(a, b, c), add(b, a, c);
}
build();
int s;
cin >> s;
while (s -- )
{
int x, y, c;
cin >> x >> y >> c;
key[g[x][y]] |= 1 << c - 1;
}
cout << bfs() << endl;
return 0;
}