Xiaocheng and Xiaohua are both good students who love mathematics. Recently, they have become addicted to Sudoku games. They want to compete with Sudoku. But ordinary Sudoku was too simple for them, so they asked Dr. Z for advice. Dr. Z took out his recently invented "target Sudoku" as the topic of the competition between the two children.

The square of target Sudoku is the same as that of ordinary Sudoku, which is 9 squares wide × Nine of the nine high squares are three wide × Three grid high small Jiugong grid (separated by thick black lines). In this big Jiugong grid, some numbers are known. According to these numbers, use logical reasoning to fill in the numbers from 1 to 9 in other spaces. Each number cannot be repeated in each small nine palace, and each number cannot be repeated in each row and column. However, target Sudoku is different from ordinary Sudoku in that each square has a score, and like a target, the closer to the center, the higher the score. (as shown in the figure)

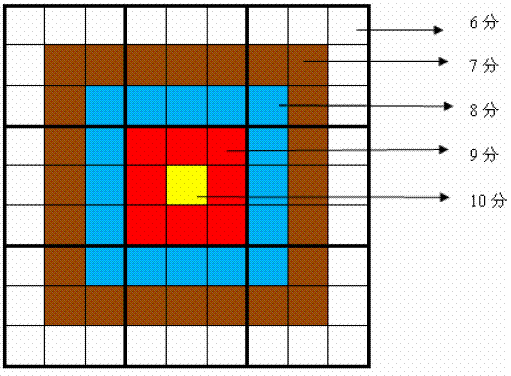
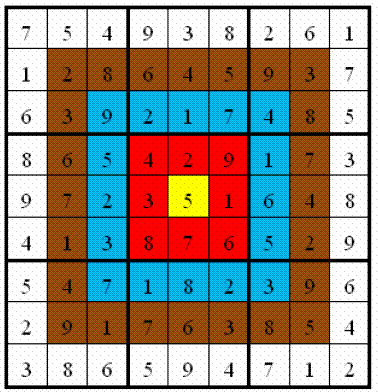
The specific score distribution in the above figure is: the innermost grid (yellow area) is 10 points, the circle outside the yellow area (red area) is 9 points, the outer circle (blue area) is 8 points, the circle outside the blue area (brown area) is 7 points, and the outermost circle (white area) is 6 points, as shown in the above figure. The requirement of the competition is that everyone must complete a given Sudoku (each given Sudoku may have different filling methods), and strive for a higher total score. The total score is the sum of the product of the score on each grid and the number filled in the corresponding grid when completing the Sudoku. As shown in the figure, in the following target Sudoku game, which has filled in numbers, the total score is 2829. The game stipulates that the winner will be determined by the total score.

Eager to win, the town found you who are good at programming and asked you to help him find the highest score for a given target Sudoku.

Nine lines altogether. 9 integers per line (each number is in the range of 0-9), indicating an unfilled Sudoku square, and the unfilled space is represented by "0". Every two numbers are separated by a space.

1 line in total. Output the highest score of target Sudoku. If the Sudoku has no solution, the integer - 1 is output.

[input / output example 2]

Output:

0 0 0 7 0 2 4 5 3
9 0 0 0 0 8 0 0 0
7 4 0 0 0 5 0 1 0
1 9 5 0 8 0 0 0 0
0 7 0 0 0 0 0 2 5
0 3 0 5 7 9 1 0 8
0 0 0 6 0 1 0 0 0
0 6 0 9 0 0 0 0 1
0 0 0 0 0 0 0 0 6

Output:

2852

[data range]

40% of the data, and the number of non-zero numbers in Sudoku is not less than 30.

80% of the data, and the number of non-zero numbers in Sudoku is not less than 26.

100% of the data, and the number of non-zero numbers in Sudoku shall not be less than 24.

[analysis]

for the first time:

Search down from the first one to find the one with the highest score.

Result: 40 points # TLE

The second time:

Search from the most in each row and column to find the one with the highest score.

Results: 75 points # there are 5 test points TLE

third time:

Search from the most in each row and column to find the one with the highest score.

In the above search, try the number a[x][y] from 1 to 9 all the time, and judge whether it can be filled every time from 1 to 9. Therefore, the judgment check in this code is actually very time-consuming. You can create an array cando [] [] (a value of 0 means that it can be filled, and a value of 1 means that it cannot be filled). Then check the number of this row and column and the number of this Jiugong lattice (assuming that it is row N and column m). If the number is not 0, the number cannot be filled in and c[a[n][m]]=1. After checking, carry out the cyclic search of 1 ~ 9: if the number c[i]=1, then continue to find the number i+1; Otherwise, search for the next number.

The AC code is as follows:

#include<bits/stdc++. h> / / Sudoku
using namespace std;
int a[11][11];
int b[11];//Maximum number of known per line
int bid[11];//id of b
int bbid;//bid number
int c[11];//Maximum known number per column
int cid[11];//id of c
int ccid;//cid number
int maxx;//Maximum score
int cando[1001][11];//Determine what number can be filled in the search
int candoid=1;//Number
bool fff=false;//Is there a solution
void checkx(int x) {//Judge which line
	for(int i=1; i<=9; i++) {
		if(a[x][i]==0)
			continue;
		cando[candoid][a[x][i]]=1;
	}
}
void checky(int y) { //Determine which column
	for(int i=1; i<=9; i++) {
		if(a[i][y]==0)
			continue;
		cando[candoid][a[i][y]]=1;
	}
}
void jggfz(int djgg) {//Change the ninth grid into the starting point (x,y) and judge the ninth grid
	int x,y;
	if(djgg==1)
		x=1,y=1;
	else if(djgg==2)
		x=1,y=4;
	else if(djgg==3)
		x=1,y=7;
	else if(djgg==4)
		x=4,y=1;
	else if(djgg==5)
		x=4,y=4;
	else if(djgg==6)
		x=4,y=7;
	else if(djgg==7)
		x=7,y=1;
	else if(djgg==8)
		x=7,y=4;
	else
		x=7,y=7;
	for(int k=x; k<x+3; k++) {
		for(int i=y; i<y+3; i++) {
			if(a[k][i]==0)
				continue;
			cando[candoid][a[k][i]]=1;
		}
	}
}
int fzfz(int x) { //Auxiliary score calculation
	if(x==5)
		return 10*a[5][5];
	int sum=0;
	for(int i=x; i<=10-x; i++)
		sum+=(5+x)*a[x][i];
	for(int i=x+1; i<=10-(x+1); i++)
		sum+=(5+x)*a[i][x];
	for(int i=x+1; i<=10-(x+1); i++)
		sum+=(5+x)*a[i][10-x];
	for(int i=x; i<=10-x; i++)
		sum+=(5+x)*a[10-x][i];
	return sum;
}
int fz() { //Calculation of score
	int sum=0;
	for(int i=1; i<=5; i++)
		sum+=fzfz(i);
	return sum;
}
void dfs(int na,int nb) { //Line number
	if(bbid==10) {
		fff=true;
		int sum=fz();
		if(sum>=maxx)
			maxx=sum;
		return;
	}
	if(a[na][nb]!=0) {
		int bbidd=bbid,ccidd=ccid;
		if(ccid==9)
			bbid++,ccid=1;
		else
			ccid++;
		dfs(bid[bbid],cid[ccid]);
		bbid=bbidd,ccid=ccidd;
		return;
	}
	//Just judge once and tell what you can fill in
	for(int i=1;i<=9;i++)
		cando[candoid][i]=0;
	int djgg=(na-1)/3*3+(nb-1)/3+1;//Use the formula to calculate the ninth house of X and y
	checkx(na);
	checky(nb);
	jggfz(djgg);
	for(int i=1; i<=9; i++) {
		if(cando[candoid][i]==1)
			continue;
		a[na][nb]=i;
		int bbidd=bbid,ccidd=ccid;
		if(ccid==9)
			bbid++,ccid=1;
		else
			ccid++;
		candoid++;
		dfs(bid[bbid],cid[ccid]);
		candoid--;
		bbid=bbidd,ccid=ccidd;
		a[na][nb]=0;
	}
}
int main() {
	for(int i=1; i<=9; i++) {
		for(int j=1; j<=9; j++) {
			scanf("%d",&a[i][j]);
			if(a[i][j]!=0)
				b[i]++;
			if(a[j][i]!=0)
				c[i]++;
		}
	}
	//Which row has the most known numbers, which row to fill in, and which column has the most known numbers, which column to fill in
	for(int i=1; i<=9; i++)
		bid[i]=i,cid[i]=i;
	for(int i=1; i<=9; i++) {
		for(int j=1; j<=9-i; j++) {
			if(b[j]<b[j+1])
				swap(b[j],b[j+1]),swap(bid[j],bid[j+1]);
			if(c[j]<c[j+1])
				swap(c[j],c[j+1]),swap(cid[j],cid[j+1]);
		}
	}
	dfs(bid[++bbid],cid[++ccid]);
	if(fff==false)
		printf("-1");
	else
		printf("%d",maxx);
	return 0;
}

The code is written for a long time and runs slowly, but it is easy to understand.