1, Simple sort
1.1 introduction to comparable interface
Compare elements, and Java provides an interface. Comparable is used to define sorting rules. Here we briefly review the comparable interface in the form of a case. (remember the customized sorting method corresponding to Comparator)
**Demand: * * 1 Define a Student class with age and name and username attributes, and provide comparison rules through the Comparable interface;
2. Define the Test class Test, and define the Test method Comparable getMax(Comparable c1,Comparable c2) in the Test class Test to complete the Test
The following shows some definitions of a Student class Student.
//1. Define a Student class with age and username attributes, and provide comparison rules through the Comparable interface;
public class Student implements Comparable<Student>{
private String username;
private int age;
public String getUsername() {
return username;
}
public void setUsername(String username) {
this.username = username;
}
public int getAge() {
return age;
}
public void setAge(int age) {
this.age = age;
}
@Override
public String toString() {
return "Student{" +
"username='" + username + '\'' +
", age=" + age +
'}';
}
@Override
public int compareTo(Student o) {
return this.getAge()-o.getAge();
}
}
Here are some test classes that define Comparable.
//2. Define the Test class Test, and define the Test method Comparable getMax(Comparable c1,Comparable c2) in the Test class Test to complete the Test
public class TestComparable {
public static void main(String[] args) {
//Create two Student objects and call the getMax method to complete the test
Student s1 = new Student();
s1.setUsername("Zhang San");
s1.setAge(18);
Student s2 = new Student();
s2.setUsername("Li Si");
s2.setAge(20);
Comparable max = getMax(s1, s2);
System.out.println(max);
}
public static Comparable getMax(Comparable c1,Comparable c2){
int result = c1.compareTo(c2);
//If result < 0, c1 is smaller than c2;
//If result > 0, c1 is greater than c2;
//If result==0, c1 is as large as c2;
if (result>=0){
return c1;
}else{
return c2;
}
}
}
1.2 bubble sorting
Bubble Sort is a relatively simple sorting algorithm in the field of computer science.
Sorting principle:
- Compare adjacent elements. If the previous element is larger than the latter, the positions of the two elements are exchanged.
- Do the same for each pair of adjacent elements, from the first pair of elements to the last pair of elements at the end. The element in the final position is the maximum value.
Requirements:
Before sorting: {4,5,6,3,2,1}
After sorting: {1,2,3,4,5,6}

Bubble sorting API design:
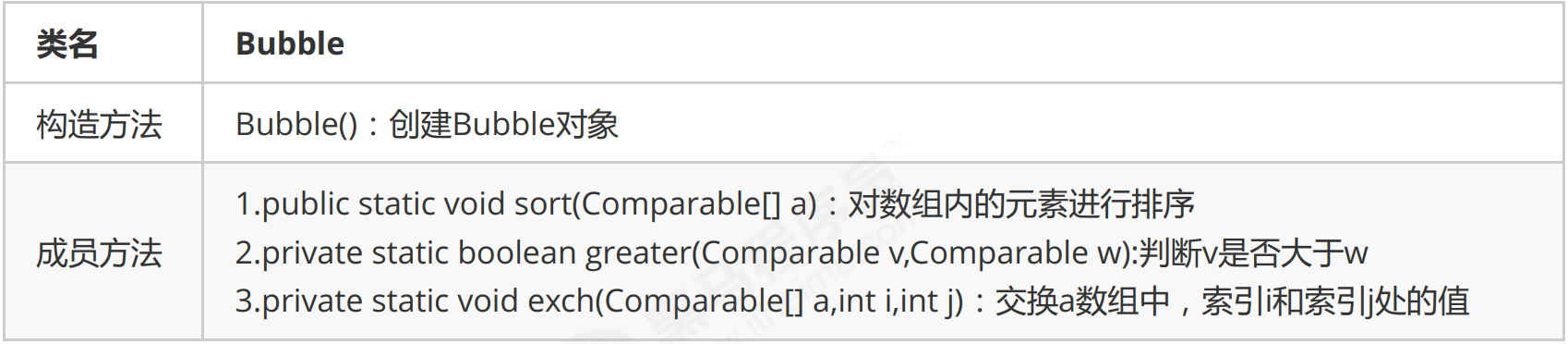
Here are some bubble sort codes that implement O(n^2).
public class Bubble {
/*
Sort the elements in array a
*/
public static void sort(Comparable[] a){
for(int i=a.length-1;i>0;i--){
for(int j=0;j<i;j++){
//{6,5,4,3,2,1}
//Compare the values at index j and index j+1
if (greater(a[j],a[j+1])){
exch(a,j,j+1);
}
}
}
}
/*
Compare whether the v element is larger than the w element
*/
private static boolean greater(Comparable v,Comparable w){
return v.compareTo(w)>0;
}
/*
Array elements i and j swap positions
*/
private static void exch(Comparable[] a,int i,int j){
Comparable temp;
temp = a[i];
a[i]=a[j];
a[j]=temp;
}
}
Some bubble sorting tests are shown below.
public class BubbleTest {
public static void main(String[] args) {
Integer[] arr = {4,5,6,3,2,1};
Bubble.sort(arr);
System.out.println(Arrays.toString(arr));//{1,2,3,4,5,6}
}
}
Here are some array implementations of bubble sorting.
public static void main(String[] args) {
int[] arr = new int[]{4,5,6,3,2,1};
//Bubble sorting
for(int i = 0;i < arr.length - 1;i++){
for (int j = 0;j < arr.length - i - 1;j++){
if (arr[j] > arr[j + 1]){
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
for (int i = 0;i < arr.length;i++){
System.out.print(arr[i] + "\t");
}
}
1.3 selection and sorting
Selective sorting is a more simple and intuitive sorting method.
Sorting principle:
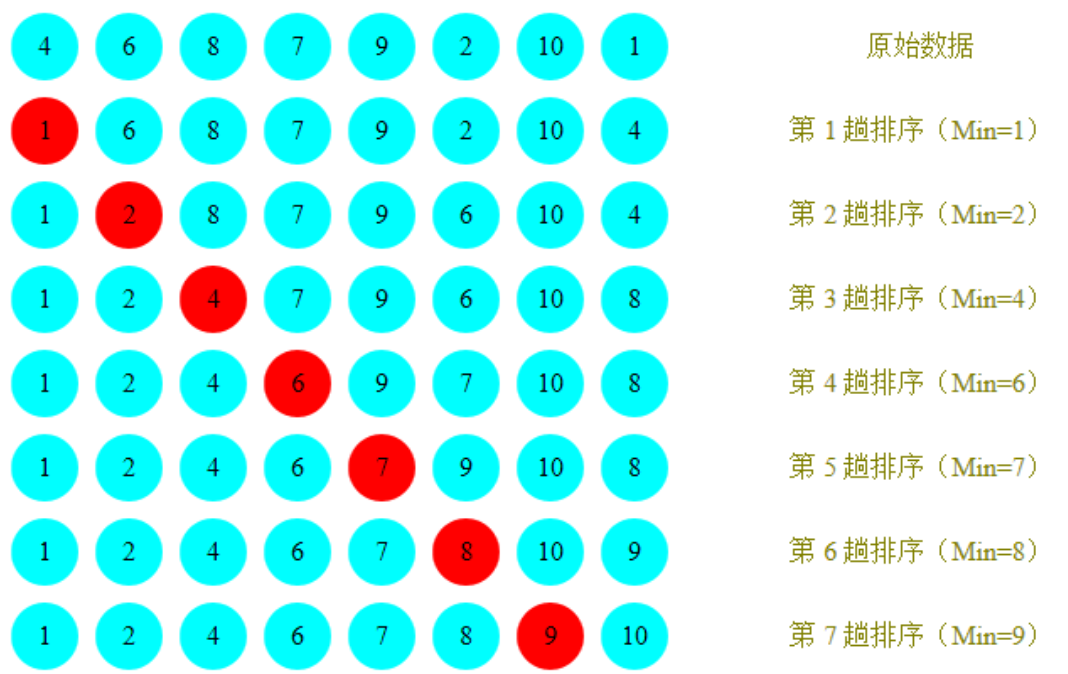
1. During each traversal, it is assumed that the element at the first index is the minimum value, which is compared with the values at other indexes in turn. If the value at the current index is greater than the value at some other index, it is assumed that the value derived from some other index is the minimum value, and finally the index where the minimum value is located can be found
2. Exchange the values at the first index and the index where the minimum value is located
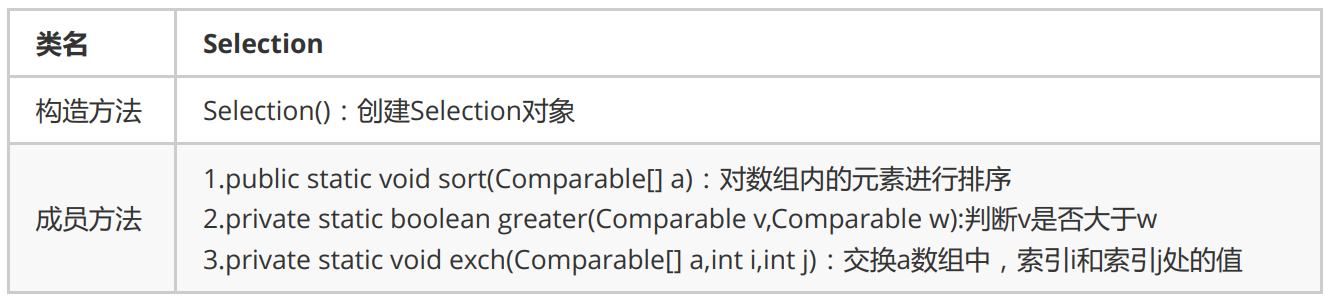
Select Sorting API design:
Requirements:
Before sorting: {4,6,8,7,9,2,10,1}
After sorting: {1,2,4,5,7,8,9,10}
Here are some quick sort implementations O (n^2).
public class Selection {
/*
Sort the elements in array a
*/
public static void sort(Comparable[] a){
for(int i=0;i<a.length -1;i++){
//Define a variable to record the index of the smallest element. By default, it is the location of the first element participating in the selection sorting
int minIndex = i;
for(int j=i+1;j<a.length;j++){
//You need to compare the value at the minimum index minIndex with the value at the j index;
if (greater(a[minIndex],a[j])){
minIndex=j;
}
}
//Swap the value at index minIndex where the smallest element is located and the value at index i
exch(a,i,minIndex);
}
}
/*
Compare whether the v element is larger than the w element
*/
private static boolean greater(Comparable v,Comparable w){
return v.compareTo(w)>0;
}
/*
Array elements i and j swap positions
*/
private static void exch(Comparable[] a,int i,int j){
Comparable temp;
temp = a[i];
a[i]=a[j];
a[j]=temp;
}
}
Here are some quick sort code tests.
public class SelectionTest {
public static void main(String[] args) {
//raw data
Integer[] a = {4,6,8,7,9,2,10,1};
Selection.sort(a);
System.out.println(Arrays.toString(a));//{1,2,4,5,7,8,9,10}
}
}
1.4 insert sort
Insertion sort is a simple, intuitive and stable sorting algorithm.
Sorting principle:
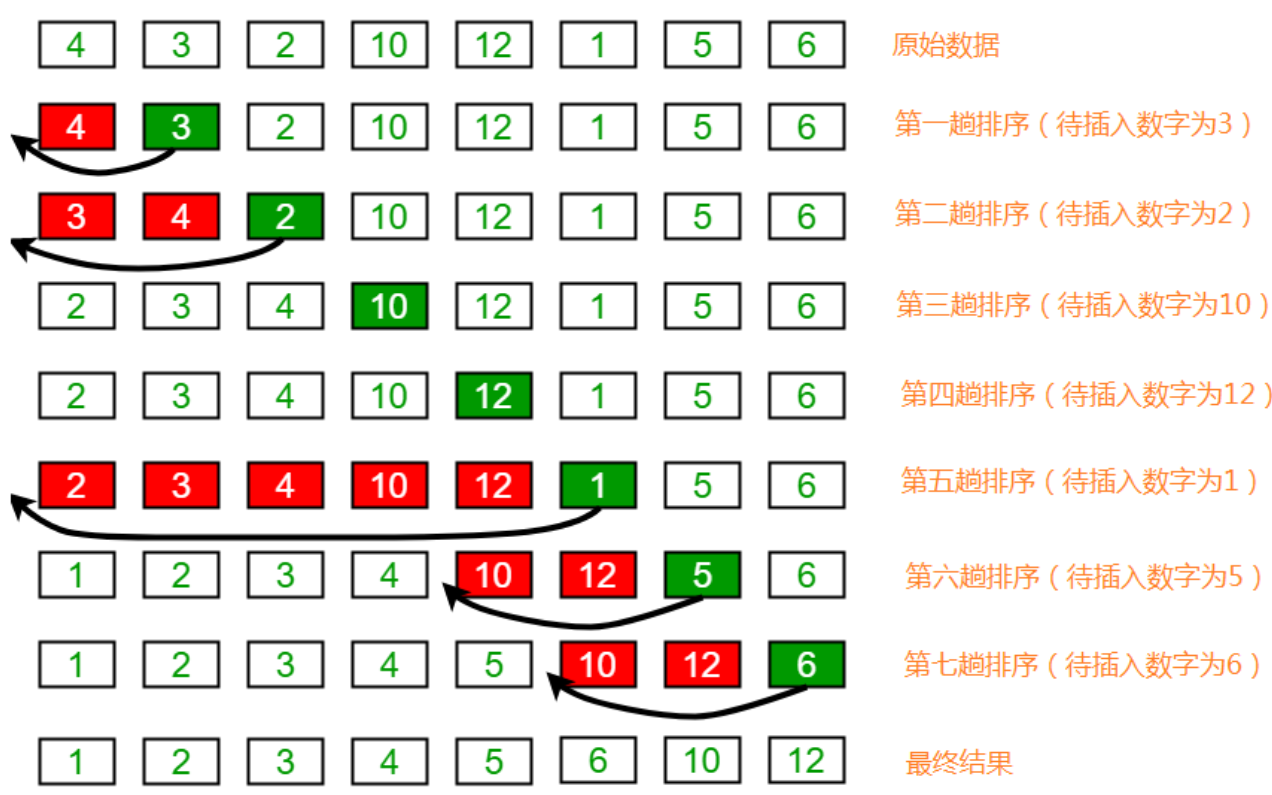
1. Divide all elements into two groups, sorted and unordered;
2. Find the first element in the unordered group and insert it into the sorted group;
3. Flashback traverses the sorted elements and compares them with the elements to be inserted in turn until an element less than or equal to the element to be inserted is found, then put the element to be inserted in this position and move the other elements one bit backward;
Insert sort API design:
The following shows some implementations of insertion sorting code, with time complexity O(n^2).
/*
1.Divide all elements into two groups, sorted and unordered;
2.Find the first element in the unordered group and insert it into the sorted group;
3.Flashback traverses the sorted elements and compares them with the elements to be inserted in turn until an element less than or equal to the element to be inserted is found
Insert the element in this position, and the other elements move back one bit;
*/
public class InsertionSort {
/*
Sort the elements in array a
*/
public static void sort(Comparable[] a){
for (int i = 1; i < a.length; i++) {
//The current element is a[i]. Compare it with the elements before I to find the elements smaller than a[i]
for (int j = i; j > 0; j--) {
if (greater(a[j - 1],a[j])){
exch(a,j - 1,j);
}else {
//If the element is found, the loop ends
break;
}
}
}
}
/*
Compare whether element a is larger than element b
*/
private static boolean greater(Comparable a, Comparable b){
return a.compareTo(b) > 0;
}
/*
Exchange position of array elements a and b
*/
private static void exch(Comparable[] a, int i,int j){
Comparable temp;
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
Here are some tests for inserting sorting.
public class InsertionTest {
public static void main(String[] args) {
Integer[] array = {4,3,2,10,12,1,5,6};
InsertionSort.sort(array);
System.out.println(Arrays.toString(array));
}
}
2, Advanced sorting
Basic sorting, including bubble sorting, selection sorting and insertion sorting, and their time complexity in the worst case is divided
Through analysis, it is found that it is O(N^2), and the square order is analyzed through our previous learning algorithm. We know that with the increase of input scale, the time cost will rise sharply, so these basic sorting methods can not deal with larger-scale problems. Next, we learn some advanced sorting algorithms to reduce the time complexity of the algorithm to the highest order power.
2.1 Hill sorting
Hill sort is a kind of insertion sort, also known as "reduced incremental sort", which is a more efficient improved version of insertion sort algorithm.
Sorting principle:
1. Select a growth amount h and group the data according to the growth amount h as the basis for data grouping;
2. Insert and sort each group of data divided into groups;
3. Reduce the growth to 1 at least, and repeat the second step.
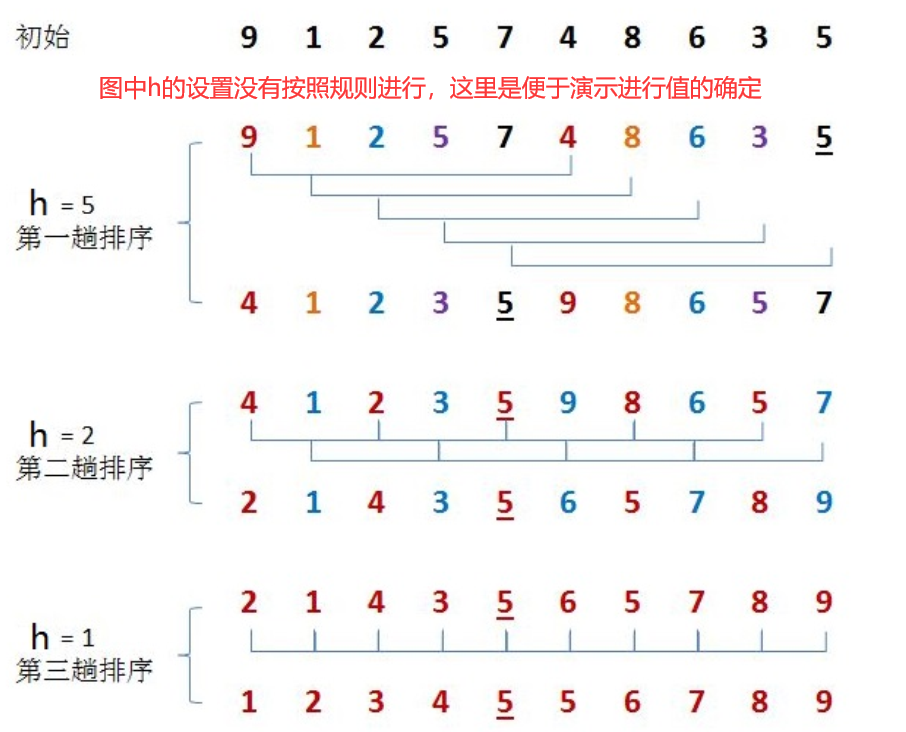
Determination of growth h
For each fixed rule of the value of growth h, we adopt the following rules:
Some determinations of growth h are shown below.
int h=1
while(h<5){
h=2h+1;//3,7
}
//At the end of the cycle, we can determine the maximum value of h;
h The reduction rules are:
h=h/2
API design for Hill sorting:
Here are some code implementations of hill sorting.
/*
1.Select a growth amount h and group the data according to the growth amount h as the basis for data grouping;
2.Insert and sort each group of data divided into groups;
3.Reduce the growth to 1 and repeat the second step.
*/
public class ShellSort {
/*
Sort the elements in array a
*/
public static void sort(Comparable[] a){
int N = a.length;
int h = 1;
//Determine the maximum value of h
while (h < N/2){
h = 2 * h + 1;
}
//When the increment h is less than 1, the sorting ends
while (h >= 1){
//Find the element to insert
for (int i = h; i < N; i++) {
//a[i] is the element to be inserted
//Need to insert a[i] into a[i - h],a[i - 2h] in
for (int j = i; j >= h ; j-=h) {
//At this time, the element to be inserted is a[j], which needs to be combined with a[j - h],a[j - 2h] For comparison, if a[j] is small, the position needs to be exchanged, otherwise it does not need to be exchanged
if (greater(a[j - h],a[j])){
exch(a,j - h,j);
}else {
break;
}
}
}
h /=2;
}
}
/*
Compare whether element a is larger than element b
*/
private static boolean greater(Comparable a, Comparable b){
return a.compareTo(b) > 0;
}
/*
Exchange position of array elements a and b
*/
private static void exch(Comparable[] a, int i,int j){
Comparable temp;
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
Here are some Hill sort code implementation tests.
public class ShellTest {
public static void main(String[] args) {
Integer[] array = {9,1,2,5,7,4,8,6,3,5};
ShellSort.sort(array);
System.out.println(Arrays.toString(array));
}
}
Time complexity analysis of Hill sort
There are many versions of the time complexity analysis of Hill sort on the Internet. Because the mathematical principles covered in it are only complex and cumbersome, in order to facilitate understanding, the post analysis method and insertion sort are compared to evaluate its performance. The test data reverse is used here_ Arr.txt file, which stores the reverse data from 100000 to 1. The test is completed according to this batch data. File Baidu cloud disk link: Link: https://pan.baidu.com/s/128RPUDuWuqMd5spBOfv5Nw
Extraction code: 1234.
Some Hill sort and other sort performance comparison test codes are shown below.
public class PerformanceTest {
//Call different test methods to complete the test
public static void main(String[] args) throws Exception {
//1. Create an ArrayList set and save the read integers
ArrayList<Integer> arrayList = new ArrayList<>();
//Create a cache read stream BufferedReader, read data, and store ArrayList
BufferedReader bufferedReader = new BufferedReader(new InputStreamReader(new FileInputStream(new File("reverse_arr.txt"))));
String line = null;
while ((line = bufferedReader.readLine()) != null){
//Line is a string. Convert line to Integer Store in collection
int i = Integer.parseInt(line);
arrayList.add(i);
}
//Turn off I/O flow
bufferedReader.close();
//3. Convert the ArrayList set into an array
Integer[] a = new Integer[arrayList.size()];
arrayList.toArray(a);
//4. Call the test code to complete the test
// testBubble(a);//46984 seconds!
// testInsertion(a);// Nine seconds!
// testMerge(a);//101 seconds!
//testQuick(a);
testSelection(a);//13600 seconds!
}
//Fake sort
public static void testBubble(Integer[] a) {
//1. Time before acquisition
long start = System.currentTimeMillis();
//2. Execute algorithm code
BubbleSort.sort(a);
//3. Time after acquisition
long end = System.currentTimeMillis();
System.out.println("The time taken for bubble sorting is:" + (end - start) + "Seconds!");
}
//Insert sort
public static void testInsertion(Integer[] a) {
//1. Time before acquisition
long start = System.currentTimeMillis();
//2. Execute algorithm code
InsertionSort.sort(a);
//3. Time after acquisition
long end = System.currentTimeMillis();
System.out.println("The time taken to insert a sort is:" + (end - start) + "Seconds!");
}
//Select sort
public static void testSelection(Integer[] a) {
//1. Time before acquisition
long start = System.currentTimeMillis();
//2. Execute algorithm code
SelectionSort.sort(a);
//3. Time after acquisition
long end = System.currentTimeMillis();
System.out.println("The time taken to select a sort is:" + (end - start) + "Seconds!");
}
//Merge sort
public static void testMerge(Integer[] a) {
//1. Time before acquisition
long start = System.currentTimeMillis();
//2. Execute algorithm code
MergeSort.sort(a);
//3. Time after acquisition
long end = System.currentTimeMillis();
System.out.println("The time taken to merge and sort is:" + (end - start) + "Seconds!");
}
//Quick sort
public static void testQuick(Integer[] a) {
//1. Time before acquisition
long start = System.currentTimeMillis();
//2. Execute algorithm code
QuickSort.sort(a);
//3. Time after acquisition
long end = System.currentTimeMillis();
System.out.println("The time taken for quick sort is:" + (end - start) + "Seconds!");
}
}
From the comparison test of the code, it can be found that the efficiency of Hill sort is much higher than that of insert sort when dealing with large quantities of data.
2.2 merge sort
2.2. 1 recursion
Definition: when defining a method, the method itself is called inside the method, which is called recursion
Function: it usually transforms a large and complex problem into a smaller problem similar to the original problem. The recursive strategy only needs a small number of programs to describe the multiple repeated calculations required in the problem-solving process, which greatly reduces the amount of code of the program.
Note: in recursion, you can't call yourself unlimited. You must have boundary conditions to end the recursion, because each recursive call will open up a new space in the stack memory and re execute the method. If the recursion level is too deep, it is easy to cause stack memory overflow.
Requirements: please define a method to calculate the factorial of N by recursion;
Here are some factorials of N using recursive completion.
// A code block var foo = 'bar';
// An highlighted block var foo = 'bar';
2.2. 2 merge sort
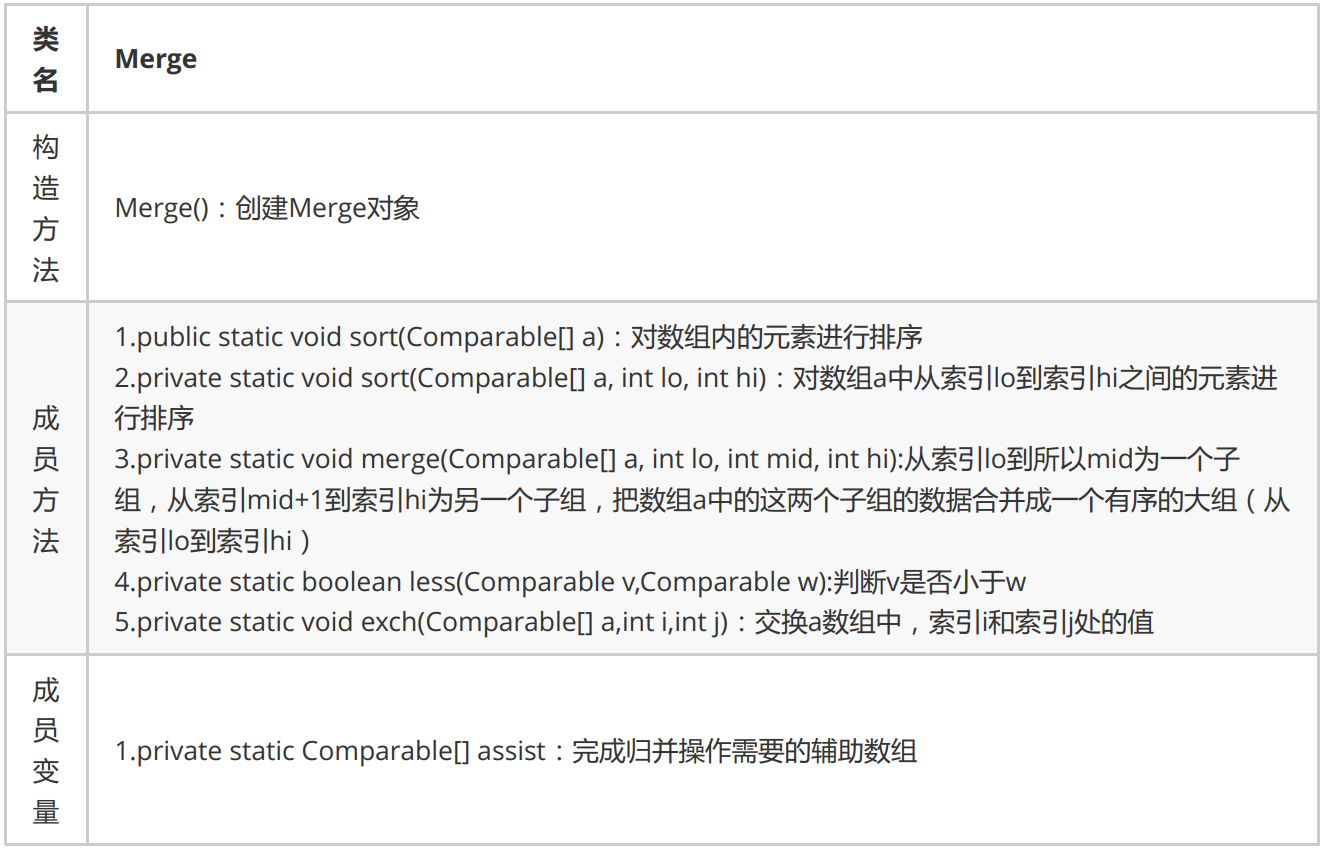
Merge sort is an effective sort algorithm based on merge operation. This algorithm is a very typical application of divide and conquer method. The ordered subsequences are combined to obtain a completely ordered sequence; That is, each subsequence is ordered first, and then the subsequence segments are ordered. If two ordered tables are merged into one, it is called two-way merging.
Sorting principle:
1. Split a set of data into two subgroups with equal elements as far as possible, and continue to split each subgroup until the number of elements in each subgroup after splitting is 1.
2. Merge two adjacent subgroups into an ordered large group;
3. Repeat step 2 until there is only one group.
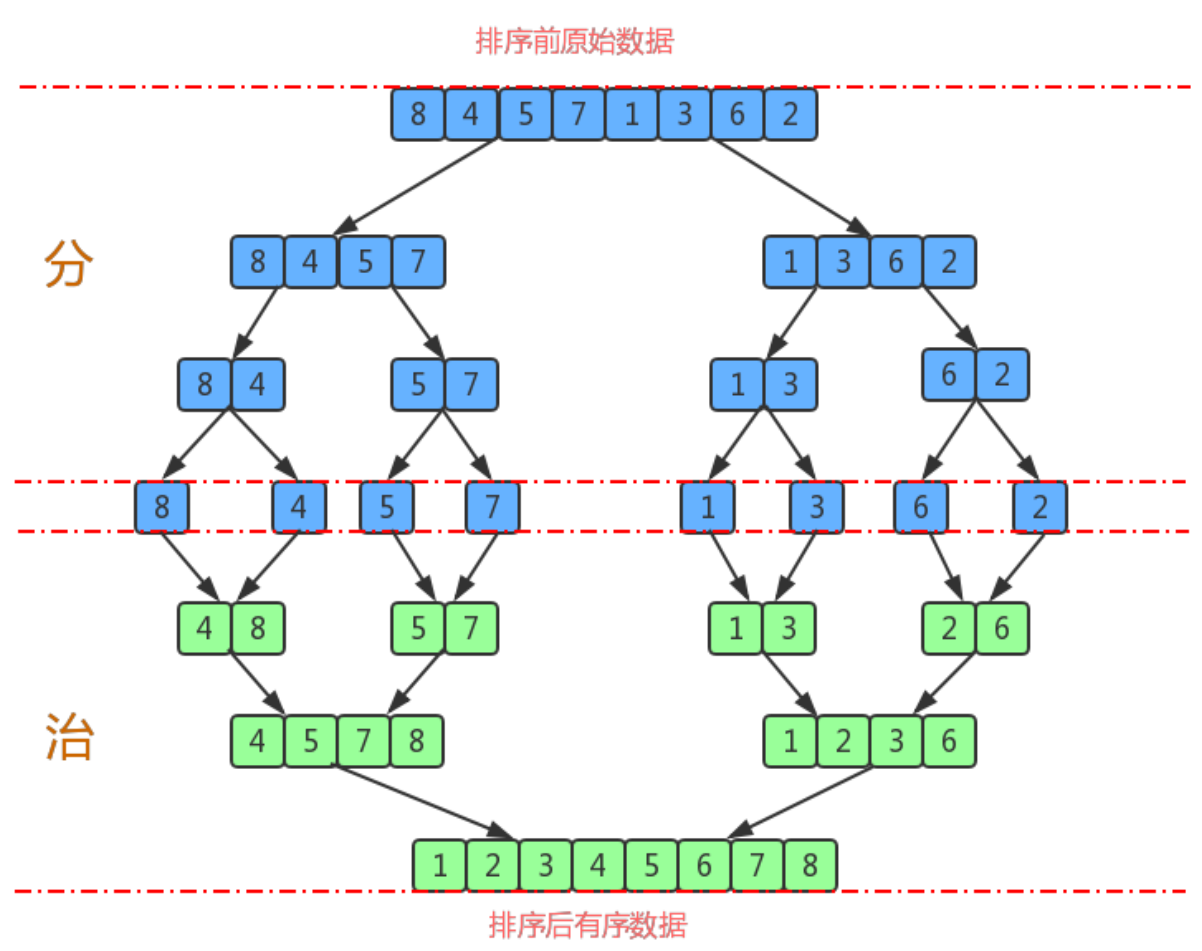
Merge and sort API design:
The following shows some merging and sorting code implementation, with time complexity O(nlogn).
/*
1.Split a set of data into two subgroups with equal elements as far as possible, and continue to split each subgroup until the number of elements in each subgroup is
1 until.
2.Merging two adjacent subgroups into an ordered large group;
3.Repeat step 2 until there is only one group.
*/
public class MergeSort {
/*
Auxiliary data required for merging
*/
private static Comparable[] assist;
/*
Sort the elements in array a (call yourself recursively)
*/
public static void sort(Comparable[] a){
//1. Initialize auxiliary array
assist = new Comparable[a.length];//Define that the length of the last sorted array is consistent with the length of the original array
//2. Define a lo variable and hi variable to record the maximum index and minimum index in the array respectively
int lo = 0;
int hi = a.length - 1;
//3. Call the sort overloaded method to sort the elements in array a from index lo to hi
sort(a,lo,hi);
}
/*
Sorts the elements in array a from index lo to index hi
*/
private static void sort(Comparable[] a,int lo,int hi){
//Assuming that the array length is 0, there is no need to sort (security check)
if (hi <= lo){
return;
}
int mid = (lo + hi) / 2;
//Sorts the elements from index lo to index mid
sort(a, lo, mid);
//Sort the elements between index mid + 1 and hi
sort(a, mid + 1, hi);
//merge the above two subgroups of lo
merge(a,lo, mid,hi);
}
/*
From index lo to index mid is a subgroup, and from index mid+1 to index hi is another subgroup,
Merge the data of the two subgroups in array a into an ordered large group (from index lo to hi)
*/
private static void merge(Comparable[] a,int lo,int mid,int hi){
//Merge the data from lo to mid and mid+1 to hi into the index corresponding to the auxiliary array assist
int i = lo;//Define a pointer to the index in the assist array that starts filling data
int p1 = lo;//Defines a pointer to the first element of the first set of data
int p2 = mid + 1;//Defines a pointer to the first element of the second set of data
//Compare the element sizes of the left and right subgroups, and fill the data into the assist array
while (p1 <= mid && p2 <= hi){
if (less(a[p1],a[p2])){
assist[i++] = a[p1++];
}else {
assist[i++] = a[p2++];
}
}
//After the above cycle, if one of the conditions P1 < = mid & & P2 < = hi is not satisfied, it means that the merging of the left group or the right group is completed
//Continue to fill the unfilled data into the assist, and execute the following cycle according to the avoidance of the left and right subgroups
while (p1 <= mid){
assist[i++] = a[p1++];
}
while (p2 <= hi){
assist[i++] = a[p2++];
}
//So far, the elements from lo to hi in the assit auxiliary array are ordered, and the data is copied to the corresponding index in the a array
for (int index = lo; index <= hi; index++) {
a[index] = assist[index];
}
}
/*
Compare whether element a is larger than element b
*/
private static boolean less(Comparable a, Comparable b){
return a.compareTo(b) < 0;
}
/*
Exchange position of array elements a and b
*/
private static void exch(Comparable[] a, int i,int j){
Comparable temp;
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
Some merge sort code implementation tests are shown below.
public class MergeTest {
public static void main(String[] args) {
Integer[] array = {4, 6, 8, 7, 9, 2, 10, 1,12};
MergeSort.sort(array);
System.out.println(Arrays.toString(array));
}
}
Merge sort time complexity analysis:
Merge sort is the most typical example of divide and conquer. In the above algorithm, a[lo... hi] is sorted. First, it is divided into a[lo... Mid] and a[mid+1... hi], which are sorted separately through recursive calls, and finally the ordered sub arrays are merged into the final sorting result. The exit of this recursion is that if an array can no longer be divided into two sub arrays, merge will be performed to determine the size of the elements and sort them when merging.
Assuming that the number of elements is n, the number of splits using merge sort is log2(n), so there are log2(n) layers. The time complexity of the final merge sort is: log2(n)* 2^(log2(n))=log2(n)*n. according to the large o derivation rule, the base number is ignored, and the time complexity of the final merge sort is O(nlogn);
Performance comparison between merge sort and Hill sort: performance comparison similar to Hill sort
Here are some performance comparisons between merge sort and Hill sort.
// A code block var foo = 'bar';
// An highlighted block var foo = 'bar';
Disadvantages of merge sorting:
When calling the merge sort algorithm, you need to apply for additional array space assist, resulting in increased space complexity. It is a typical space for time operation. This problem can be ignored in Java program development, but in the process of embedded development, the merging and sorting algorithm should be used carefully.
2.3 quick sort
Quick sort is an improvement of bubble sort. Its basic idea is to divide the data to be sorted into two independent parts through one-time sorting. All the data in one part is smaller than all the data in the other part, and then quickly sort the two parts of data according to this method. The whole sorting process can be recursive, so that the whole data becomes an ordered sequence.
Sorting principle:
1. First, set a boundary value, and divide the array into left and right parts through the boundary value;
2. Put the data greater than or equal to the boundary value to the right of the array, and the data less than the boundary value to the left of the array. At this time, all elements in the left part are less than or equal to the boundary value, while all elements in the right part are greater than or equal to the boundary value;
3. Then, the data on the left and right can be sorted independently. For the array data on the left, you can take another boundary value and divide this part of the data into left and right parts. Similarly, place the smaller value on the left and the larger value on the right. The array data on the right can also be processed similarly.
4. By repeating the above process, it can be seen that this is a recursive definition. After the left part is sorted recursively, the right part is sorted recursively. When the data of the left and right parts are sorted, the sorting of the whole array is completed.
Quicksort API design:

Segmentation principle:
The basic idea of dividing an array into two subarrays:
1. Find a reference value and point to the head and tail of the array with two pointers respectively;
2. Search for an element smaller than the reference value from the tail to the head, stop the search, and record the position of the pointer;
3. Search for an element larger than the reference value from the head to the tail, stop the search, and record the position of the pointer;
4. Exchange the elements of the current left pointer position and the right pointer position;
5. Repeat steps 2, 3 and 4 until the value of the left pointer is greater than that of the right pointer.
Some quick sort code implementations are shown below.
/*
1.First, set a boundary value, and divide the array into left and right parts through the boundary value;
2.Put the data greater than or equal to the boundary value to the right of the array, and the data less than the boundary value to the left of the array. At this time, each element in the left part is less than
Or equal to the boundary value, and all elements in the right part are greater than or equal to the boundary value;
*/
public class QuickSort {
/*
Compare whether element a is larger than element b
*/
private static boolean less(Comparable a, Comparable b){
return a.compareTo(b) < 0;
}
/*
Exchange position of array elements a and b
*/
private static void exch(Comparable[] a, int i,int j){
Comparable temp;
temp = a[i];
a[i] = a[j];
a[j] = temp;
}
/*
Sort the elements in array a
*/
public static void sort(Comparable[] a){
int lo = 0;
int hi = a.length - 1;
sort(a,lo,hi);
}
private static void sort(Comparable[] a,int lo,int hi){
//Validate the array
if (hi <= lo){
return;
}
//Slice array a from lo to hi
//The elements in the array from lo index to hi index need to be grouped
int partition = partition(a, lo, hi);
//Sort left progeny
sort(a,lo,partition - 1);
//Sort right subgroup
sort(a,partition + 1,hi);
}
//For array a, from index lo to
public static int partition(Comparable[] a,int lo,int hi){
Comparable key = a[lo];//Take the element with index 0 as the base value
int left = lo;//Define a left pointer, and the initial pointer points to the leftmost element
int right = hi + 1;//Define a right pointer. The initial pointer points to the rightmost bit of the rightmost element
//segmentation
while (true){
//Scan from right to left to find a value smaller than the reference value
while (less(key,a[--right])){
if (right == lo){
break;
}
}
//Scan from left to right to find a value larger than the reference value
while (less(a[++left],key)){
if (left == hi){
break;
}
}
if (left >= right){
break;//End of scan
}else {
//Swap elements at left and right indexes
exch(a,right,left);
}
}
//Exchange the value at the index of the last rirht pointer and the index where the reference value is located
exch(a,lo,right);
return right;//Return right. This is the index value limit of the shard
}
}
Here are some quick sort code implementation tests.
public class QuickTest {
public static void main(String[] args) {
Integer[] array = {4, 6, 8, 7, 9, 2, 10, 1,12,10};
QuickSort.sort(array);
System.out.println(Arrays.toString(array));
}
}
Quick sort time complexity analysis:
The first segmentation of quick sort starts from both ends and searches alternately until left and right coincide. Therefore, the time complexity of the first segmentation algorithm is O(n), but the time complexity of the whole quick sort is related to the number of segmentation.
Optimal case: the benchmark number selected for each segmentation just divides the current sequence equally. In the optimal case, the time complexity of quick sorting is O(nlogn);
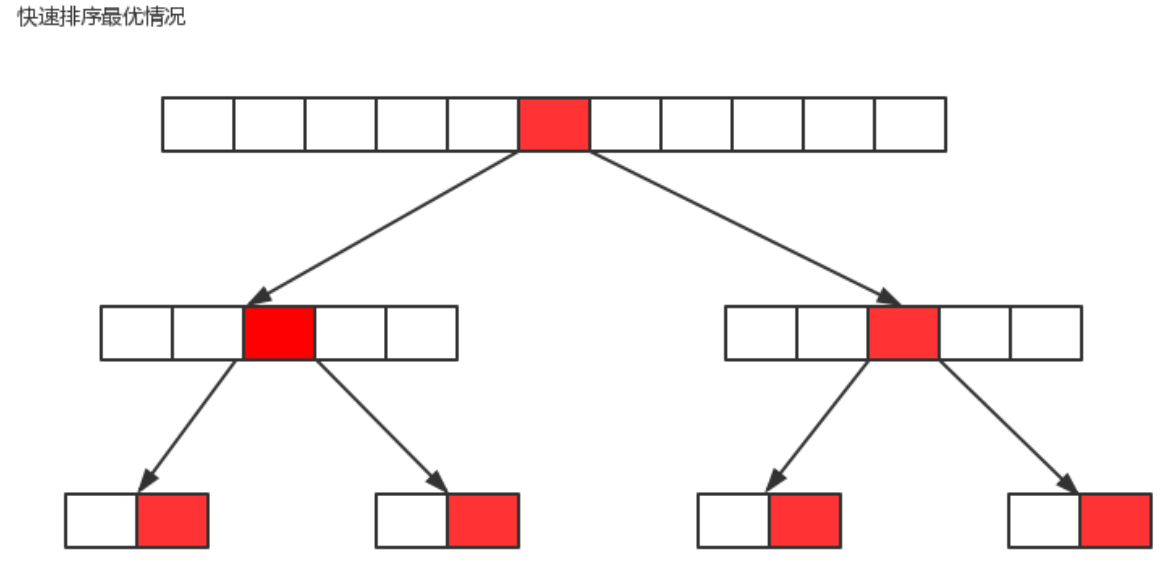
Worst case: the benchmark number selected for each segmentation is the maximum number or the minimum number in the current sequence, so that each segmentation will have a subgroup, so it will be segmented n times in total. Therefore, in the worst case, the time complexity of quick sorting is O(n^2);
Similarities and differences between quick sort and merge sort:
Quick sort is another divide and conquer sorting algorithm. It divides an array into two sub arrays and sorts the two parts independently. Quick sort and merge sort are complementary: merge sort divides the array into two sub arrays, sorts them respectively, and merges the ordered sub arrays to sort the whole array. The way of quick sort is that when the two arrays are ordered, the whole array is naturally ordered. In merge sort, an array is equally divided into two parts. The merge call occurs before processing the whole array. In quick sort, the position of the split array depends on the content of the array, and the recursive call occurs after processing the whole array.
2.4 stability of sorting
Definition of stability:
There are several elements in array arr, in which element A is equal to element B, and element A is in front of element B. If A sorting algorithm is used to sort, it can ensure that element A is still in front of element B, it can be said that the algorithm is stable.
Meaning of stability:
If a group of data only needs to be sorted once, the stability is generally meaningless. If a group of data needs to be sorted multiple times, the stability is meaningful. For example, the content to be sorted is a group of commodity objects. The first sorting is sorted by price from low to high, and the second sorting is sorted by sales volume from high to low. If the stability algorithm is used in the second sorting, objects with the same sales volume can still be displayed in the order of price, and only objects with different sales volumes need to be reordered. This can not only maintain the original meaning of the first sorting, but also reduce the system overhead.
Stability of common sorting algorithms:
Bubble sort:
Only when arr [i] > arr [i + 1], the positions of elements will be exchanged, and when they are equal, they will not be exchanged. Therefore, bubble sorting is a stable sorting algorithm.
Select sort:
Selective sorting is to select the smallest current element for each position, such as data {5 (1), 8, 5 (2), 2, 9}. The smallest element selected for the first time is 2, so 5 (1) will exchange positions with 2. At this time, when 5 (1) comes after 5 (2), the stability is destroyed. Therefore, selective sorting is an unstable sorting algorithm.
Insert sort:
The comparison starts from the end of the ordered sequence, that is, the element you want to insert is compared with the largest one that has been ordered. If it is larger than it, it is directly inserted behind it. Otherwise, look forward until you find its insertion position. If you encounter an element that is equal to the inserted element, put the element to be inserted after the equal element. Therefore, the sequence of equal elements has not changed. The order out of the original unordered sequence is the order after the order is arranged, so the insertion sort is stable.
Hill sort:
Hill sort is to insert and sort the elements according to the asynchronous length. Although one insertion sort is stable and will not change the relative order of the same elements, in different insertion sort processes, the same elements may move in their own insertion sort, and finally their stability will be disturbed. Therefore, Hill sort is unstable.
Merge sort:
Merge sort in the process of merging, the position will be exchanged only when arr [i] < arr [i + 1]. If the two elements are equal, the position will not be exchanged, so it will not destroy the stability. Merge sort is stable.
Quick sort:
Quick sort requires a benchmark value. Find an element smaller than the benchmark value on the right side of the benchmark value and an element larger than the benchmark value on the left side of the benchmark value, and then exchange the two elements. At this time, the stability will be destroyed. Therefore, quick sort is an unstable algorithm.