2009 Niuke Summer Multi-School Training (Game 9) J-Symmetrical Painting

Daily worship:
Worship Xin Da Hao Ma and Bowen Big Man

meaning of the title

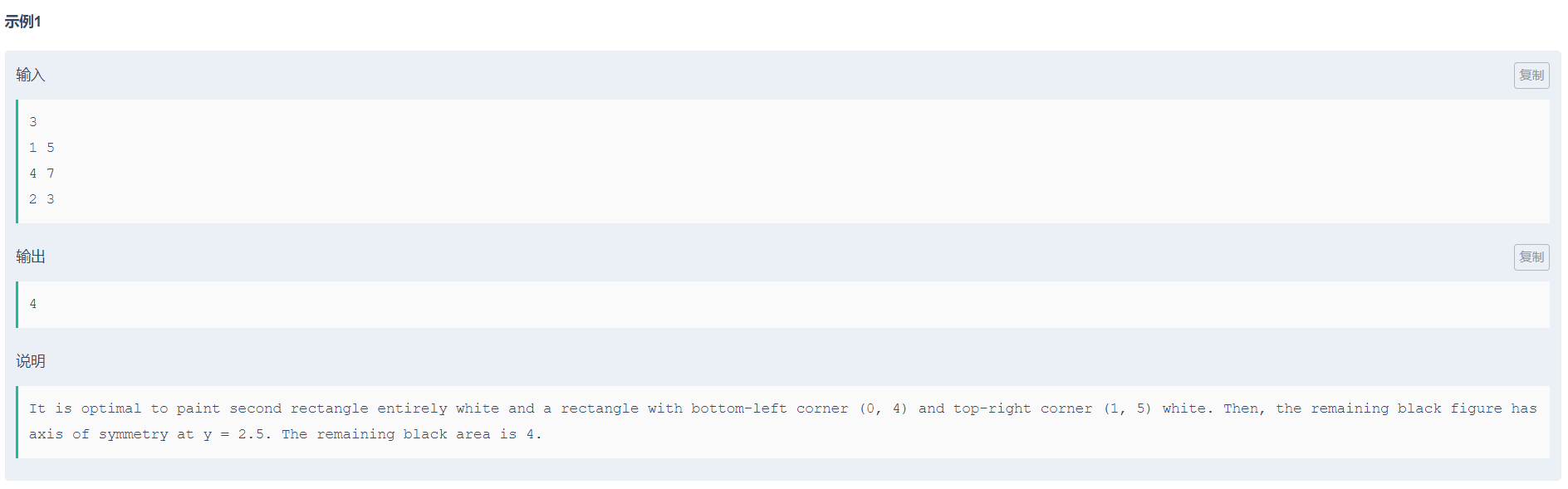
Given n n n rectangles with a width of 1, some areas are deleted so that the remaining figures have a symmetrical axis parallel to the x-axis. How can we maximize the area and output the largest area?

thinking

It is easy to see that the symmetric axis can only appear at both ends or at the midpoint of the rectangle. (If not at these three points, there will be no sudden change in area, i.e., no extreme point)
Scanning lines are used to sweep through these possible points one by one, calculate the area and get the maximum value.

Pit point

Unexpected

Code

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

const int N=3e5+5;

double top[N],down[N];
double mid[N];
double all[3*N];

int main()
{
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        scanf("%lf%lf",&down[i],&top[i]);
        mid[i]=(down[i]+top[i])/2;
        all[3*i]=down[i];
        all[3*i+1]=top[i];
        all[3*i+2]=mid[i];
    }
    sort(down,down+n);
    sort(mid,mid+n);
    sort(top,top+n);
    sort(all,all+3*n);
//    for(int i=0;i<n;i++)
//    {
//        cout<<down[i]<<' ';
//    }
//    cout<<endl;
//    for(int i=0;i<n;i++)
//    {
//        cout<<mid[i]<<' ';
//    }
//    cout<<endl;
//    for(int i=0;i<n;i++)
//    {
//        cout<<top[i]<<' ';
//    }
//    cout<<endl;
//    for(int i=0;i<3*n;i++)
//    {
//        cout<<all[i]<<' ';
//    }
//    cout<<endl;
    int cntdown=0,cntmid=0,cnttop=0;
    int num1=0,num2=0;
    double maxn=0;
    double sum=0;
    for(int lin=1;lin<3*n;lin++)
    {
        while(cntdown<n&&down[cntdown]<all[lin])
        {
            cntdown++;
            num1++;
        }
        while(cntmid<n&&mid[cntmid]<all[lin])
        {
            cntmid++;
            num1--;
            num2++;
        }
        while(cnttop<n&&top[cnttop]<all[lin])
        {
            cnttop++;
            num2--;
        }
        sum=sum+num1*(all[lin]-all[lin-1])-num2*(all[lin]-all[lin-1]);
        maxn=max(maxn,sum);
    }
    printf("%lld\n",(ll)(2*maxn));
    return 0;
}