To tell you the truth, I really don't want to write. I did badly in the exam. 35 points, rank34/55
But reflection, problem-solving are still to be written.
When I saw the "template" of T2 in the exam, it was absolutely not so simple. I jumped directly. It took two hours to make T1 first, and more than one hour to make T3. So T2 lost. As a result, T3 exploded zero, and the T1 of self-perceived AC only took 35.
Summarize a few points:
1. Never place your hopes on a particular topic, let alone stumble on it.
2. Grasp the time allocation, as Deepinc said, first evaluate the difficulty, about half an hour or so to get the simplest out, to think about the harder, half an hour without thinking about what to do.
3. Lower expectations, less chances of disappointment. You can take Rank1 QWQ if you step on your blog crazily.
T1 Spicy Chicken
n^2 Storm Search, there are (x-1)*(y-1) hydrogen bonds in a (x*y) block. Then discuss the number of hydrogen bonds between blocks and blocks. The number of blocks in contact is (d-1)*2. If there is one end out of the block except the contact part+1,
With two ends in the head + 2
Ps: Think carefully and don't miss anything.
Pss: Make sure to draw in the form of the coordinate system given in the question. For example, the question x is the abscissa and y is the ordinate. Don't flip the coordinate system like I did. Sort by y and get stuck.
#include<iostream> #include<cstdio> #include<algorithm> using namespace std; #define ll long long int n; struct node{ ll u,l,d,r; }q[110000]; inline int cmp(node a,node b){ return a.l<b.l; } long long ans; int main(){ scanf("%d",&n); for(register int i=1;i<=n;i++){ scanf("%lld%lld%lld%lld",&q[i].l,&q[i].d,&q[i].r,&q[i].u); ans+=(ll)(q[i].u-q[i].d)*(q[i].r-q[i].l)*2; } //cout<<ans<<endl; sort(q+1,q+n+1,cmp); for(register int i=1;i<n;i++){ for(register int j=i+1;j<=n&&q[i].r+1>=q[j].l;j++){ int minn; // cout<<i<<" "<<j<<endl; if(q[j].l==q[i].l){ if(q[j].u+1==q[i].d||q[j].d-1==q[i].u){ minn=min(q[i].r-q[i].l+1,q[j].r-q[j].l+1); ans+=(minn-1)*2; if(q[j].r!=q[i].r) ans++; } } else if(q[j].l<=q[i].r){ if(q[j].u+1==q[i].d||q[j].d-1==q[i].u){ if(q[j].r>q[i].r) minn=q[i].r-q[j].l+1; else if(q[j].r<q[i].r) minn=q[j].r-q[j].l+1; else minn=q[i].r-q[j].l+1; ans+=(minn-1)*2; ans+=(q[j].r==q[i].r)?1:2; } } else if(q[i].r+1==q[j].l){ if(q[j].u==q[i].d-1||q[j].d==q[i].u+1) ans++; else if(q[j].u<q[i].u&&q[j].u>=q[i].d){ if(q[j].d>q[i].d) minn=q[j].u-q[j].d+1; else if(q[j].d<q[i].d) minn=q[j].u-q[i].d+1; else if(q[j].d==q[i].d) minn=q[j].u-q[i].d+1; ans+=(minn-1)*2; ans+=(q[j].d==q[i].d)?1:2; } else if(q[j].u>q[i].u&&q[i].u>=q[j].d){ if(q[j].d>q[i].d) minn=q[i].u-q[j].d+1; else if(q[j].d<q[i].d) minn=q[i].u-q[i].d+1; else if(q[j].d==q[i].d) minn=q[i].u-q[j].d+1; ans+=(minn-1)*2; ans+=(q[j].d==q[i].d)?1:2; } else if(q[j].u==q[i].u){ if(q[j].d>q[i].d) minn=q[i].u-q[j].d+1; else if(q[j].d<q[i].d) minn=q[i].u-q[i].d+1; else minn=q[i].u-q[i].d+1; ans+=(minn-1)*2; ans+=(q[j].d==q[i].d)?0:1; } } } } printf("%lld\n",ans); }
T2 template
Line segment tree maintains the number of interval balls, the number of colors, and the number of query balls is the interval of the number of barrels (from 1 to?) Number of colors
Colors should be discretized because they have negative numbers and may have large color values.
Segment trees are merged heuristically, i.e. retaining the information of the largest subtree and updating the information of the current node with other subtrees
PS: Pay attention to the answer statistics and recursive boundaries of the query function, otherwise it will be dead cycle.
PS: Note that each time a node is processed and the information of the node is not retained, it is best to clear with a timestamp (i.e. f-lazy marker), and must not use memset.
#include<iostream> #include<cstdio> #include<vector> #include<cstring> #include<algorithm> #include<map> using namespace std; int n,m,Q,num,cet,root; const int maxn=1e5+100; int ls[410000],rs[410000],f[410000],qiunum[410000],colornum[410000],w[maxn],size[maxn],ma[maxn],is_here[maxn],loc[maxn],wolan[maxn],key[maxn]; vector<int>son[110000],point[110000]; int tmp[maxn],ans[maxn]; inline void down(int t){ qiunum[ls[t]]=colornum[ls[t]]=0; qiunum[rs[t]]=colornum[rs[t]]=0; f[ls[t]]=f[rs[t]]=1; if(ls[ls[t]]==0&&rs[ls[t]]==0) f[ls[t]]=0; if(ls[rs[t]]==0&&rs[rs[t]]==0) f[rs[t]]=0; f[t]=0; } inline void build(int &t,int l,int r){ if(!t) t=++cet; if(l==r) return ; int mid=(l+r)/2; build(ls[t],l,mid); build(rs[t],mid+1,r); } inline void dfs1(int x,int pre){ size[x]=1+point[x].size(); int mxn=0; for(register int i=0;i<son[x].size();i++){ int y=son[x][i]; if(y==pre) continue; dfs1(y,x); size[x]+=size[y]; if(size[y]>mxn) ma[x]=y,mxn=size[y]; } } inline void change(int t,int l,int r,int x){ if(l==r){ colornum[t]=0; return; } if(f[t]) down(t); int mid=(l+r)/2; if(mid>=x) change(ls[t],l,mid,x); else change(rs[t],mid+1,r,x); qiunum[t]=qiunum[ls[t]]+qiunum[rs[t]]; colornum[t]=colornum[ls[t]]+colornum[rs[t]]; } int landenum; inline void add(int t,int l,int r,int x,int k){ if(l==r){ qiunum[t]+=k; colornum[t]+=k; if(wolan[w[l]]!=landenum) wolan[w[l]]=0,is_here[w[l]]=0,loc[w[l]]=0; if(k==1&&!is_here[w[l]]) is_here[w[l]]=1,loc[w[l]]=l,wolan[w[l]]=landenum; else if(k==1&&is_here[w[l]]){ if(loc[w[l]]<l) colornum[t]=0; else{ change(1,1,m,loc[w[l]]); loc[w[l]]=l; } } return; } if(f[t]) down(t); int mid=(l+r)/2; if(mid>=x) add(ls[t],l,mid,x,k); else add(rs[t],mid+1,r,x,k); qiunum[t]=qiunum[ls[t]]+qiunum[rs[t]]; colornum[t]=colornum[ls[t]]+colornum[rs[t]]; } inline void go_add(int x,int pre,int k){ for(register int i=0;i<point[x].size();i++) add(1,1,m,point[x][i],k); for(register int i=0;i<son[x].size();i++) if(son[x][i]!=pre) go_add(son[x][i],x,k); } inline int ask(int t,int x){ if(x==0) return 0; if(qiunum[t]==0) return 0; if(t==0) return 0; if(qiunum[t]<x) return colornum[t]; if(qiunum[t]==x) return colornum[t]; if(qiunum[ls[t]]==x) return colornum[ls[t]]; else if(qiunum[ls[t]]>x) return ask(ls[t],x); return colornum[ls[t]]+ask(rs[t],x-qiunum[ls[t]]); } inline void dfs(int x,int keep,int pre){ landenum++; for(register int i=0;i<son[x].size();i++){ int y=son[x][i]; if(y==pre||y==ma[x]) continue; dfs(y,0,x); } if(ma[x]) dfs(ma[x],1,x); for(register int i=0;i<point[x].size();i++) add(1,1,m,point[x][i],1); for(register int i=0;i<son[x].size();i++){ int y=son[x][i]; if(y==pre||y==ma[x]) continue; go_add(son[x][i],x,1); } ans[x]=ask(1,tmp[x]); if(!keep){ f[1]=1,qiunum[1]=0,colornum[1]=0; } } int main(){ scanf("%d",&n); int x,y; for(register int i=1;i<n;i++){ scanf("%d%d",&x,&y); son[x].push_back(y); son[y].push_back(x); } for(register int i=1;i<=n;i++) scanf("%d",&tmp[i]); scanf("%d",&m); build(root,1,m); for(register int i=1;i<=m;i++){ scanf("%d%d",&x,&y); w[i]=key[i]=y; point[x].push_back(i); } cout<<endl; sort(key+1,key+m+1); int q=unique(key+1,key+m+1)-key- 1; for(register int i=1;i<=m;i++){ w[i]=lower_bound(key+1,key+q+1,w[i])-key; } dfs1(1,0); dfs(1,0,0); scanf("%d",&Q); while(Q--){ scanf("%d",&x); printf("%d\n",ans[x]); } return 0; }
T3 Big Guy
There is an idea of complete combinatorial mathematics. For the difficulty of n questions, the number of solutions is n^m, and each solution corresponds to the first day... The next day... On the third day... Situation
So every day's plan is the same, and the probability is the same. The n-day expectation is the one-day expectation multiplied by the n-day expectation.
Another way to understand it is to call it the law of combination of addition and addition.
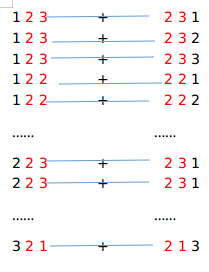
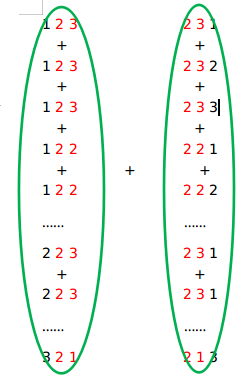
It seems intuitively that the two are equal.
So the n-day expectation is equal to the one-day expectation multiplied by the n-day expectation.
#include<iostream> #include<cstdio> #include<cstring> using namespace std; #define ll long long const int mod=1e9+7; int n,m,k; ll wt[650],f[2][450],sum; ll pow(ll a,ll b){ ll ans=1; a%=mod; while(b){ if(b&1) ans=ans*a%mod; b>>=1; a=a*a%mod; } return ans%mod; } int main(){ scanf("%d%d%d",&n,&m,&k); if(k>n){ puts("0"); return 0; } for(int i=1;i<=m;i++){ scanf("%lld",&wt[i]); if(i!=1) wt[i]=wt[i]%mod*(pow(i,k)-pow(i-1,k)+mod)%mod; sum=(sum+wt[i])%mod; } ll ans=pow(pow(m,k),mod-2)%mod; printf("%lld\n",sum*(n-k+1)%mod*ans%mod); }