Introduction
Knowledge points involved
Thinking, multiplicative inverse, combinatorial mathematics, topological sorting, DP, bipartite graph, maximum weight matching, plane geometry
Link: Nanjing 2019 regional competition [Cloned]
subject
A
Give a positive integer n and find the smallest integer k to make the set { 1 , 2 , ... n } \{1,2,\dots n\} Any size of {1,2,... n} is k k There are at least two elements in the subset of k, so that one of them is the factor of the other
Idea: at first, I thought it was a prime number plus 1, but later I found a counterexample:
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
1,2,3,4,5,6,7,8,9
1,2,3,4,5,6,7,8,9, if you add one to the number of primes, then the size of k is 5, but you can find it
{
5
,
6
,
7
,
8
,
9
}
\{5,6,7,8,9\}
{5,6,7,8,9} This set does not satisfy the condition
The simplest way is to find the law directly. You can find that the size of k is
2
,
3
,
3
,
4
,
4
...
2,3,3,4,4\dots
2,3,3,4,4... The result is
(
n
+
1
)
/
2
+
1
(n+1)/2+1
(n+1)/2+1
code
#include <bits/stdc++.h>
#define ll long long
#define INF 0x3f3f3f3f
using namespace std;
int T,n;
int main() {
cin.tie(0);
ios::sync_with_stdio(0);
cin >>T;
while(T--) {
cin >>n;
cout <<(n+1)/2+1<<endl;
}
return 0;
}
C
Main idea of the topic: give a numerical matrix, and define the path: the elements must be strictly increased from the starting grid to the end, with a tolerance of 1, and can not be expanded after the end. The number of grids shall not be less than 4 to calculate the number of paths
Idea: it's right to consider from the direction of the number of schemes at the beginning, but there are problems in the statistics of 4 and more than 4 paths. Finally, after reading the problem solution, we know that we ignore a more important point: it can't be expanded after the end point, but we can take 4, 5, etc. from the end point forward, that is, a path with length of 7 can create a path with length of 4, 5, 6, 7, In fact, 4 can be regarded as a whole
set up
d
p
[
i
]
[
j
]
[
k
]
dp[i][j][k]
dp[i][j][k]
(
i
,
j
)
(i,j)
(i,j) is the number of paths with the end point and the length of k, and this recursive formula can be obtained:
d
p
[
i
]
[
j
]
[
k
]
=
d
p
[
i
]
[
j
]
[
k
]
+
d
p
[
i
′
]
[
j
′
]
[
k
−
1
]
dp[i][j][k]=dp[i][j][k]+dp[i'][j'][k-1]
dp[i][j][k]=dp[i][j][k]+dp[i′][j′][k−1],
(
i
′
,
j
′
)
(i',j')
(i ', j') yes
(
i
,
j
)
(i,j)
(i,j), the difference of elements is 1, and
(
i
,
j
)
(i,j)
(i,j) larger data
After basically determining the method and definition of dp, the next step is to determine the order of dp. For any path, the first point must not be smaller than other adjacent points. Then you can use the concept of out degree and in degree in DAG. There is an adjacent lattice 1 larger than the point, the out degree of the point is + 1, there is an adjacent lattice 1 smaller than the point, and the in degree of the point is - 1. Then you can sort by topology, Construct the number of feasible schemes under different path lengths. See the code for the rest
code
#include <bits/stdc++.h>
#define ll long long
#define INF 0x3f3f3f3f
using namespace std;
int n,m,in[1212][1212],out[1212][1212],maze[1212][1212],Next[4][2]= {0,1,1,0,0,-1,-1,0};
ll res,dp[1212][1212][5];
const int mod=1e9+7;
struct node {
int x,y;
};
void BFS() {
queue<node>q;
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
if(!in[i][j]) {//Enter the node with penetration of 0 and prepare the topology BFS
q.push({i,j});
dp[i][j][1]=1;
}
while(!q.empty()) {
auto t=q.front();
q.pop();
int x=t.x,y=t.y;
for(int i=0; i<4; i++) {
int xx=x+Next[i][0],yy=y+Next[i][1];
if(xx<1||yy<1||xx>n||yy>m)continue;
if(maze[xx][yy]==maze[x][y]+1) {//Adjacency points can be expanded and the corresponding number of schemes can be updated
dp[xx][yy][2]=(dp[x][y][1]+dp[xx][yy][2])%mod;//The number of schemes with adjacency point length of 2 comes from the scheme with (x,y) length of 1
dp[xx][yy][3]=(dp[x][y][2]+dp[xx][yy][3])%mod;//The number of schemes with adjacency point length of 3 comes from the scheme with (x,y) length of 2
dp[xx][yy][4]=(dp[x][y][3]+dp[xx][yy][4]+dp[x][y][4])%mod;
//The number of schemes with the length of adjacent points greater than or equal to 4 comes from the number of schemes with the length of (x,y) 3 and the number of schemes greater than or equal to 4
if(--in[xx][yy]==0)q.push({xx,yy});//Topological sorting, and a new root node appears
}
}
}
}
int main() {
cin.tie(0);
ios::sync_with_stdio(0);
cin >>n>>m;
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
cin >>maze[i][j];
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
for(int k=0; k<4; k++) {
int x=i+Next[k][0],y=j+Next[k][1];
if(x<1||y<1||x>n||y>m)continue;
if(maze[i][j]==maze[x][y]+1)in[i][j]++;//Statistical input and output
if(maze[i][j]==maze[x][y]-1)out[i][j]++;//ditto
}
BFS();//Number of broad search statistical schemes
for(int i=1; i<=n; i++)
for(int j=1; j<=m; j++)
if(!out[i][j])res=(res+dp[i][j][4])%mod;
//For a point with an exit of 0, count the number of schemes whose length is greater than or equal to 4
cout <<res;
return 0;
}
H
Main idea of the title: a needs to find B. There are three types of people who support a to find B (including a). It doesn't matter if they don't support it. Everyone (except a) is in different rooms. For everyone, you can ask three kinds of questions: what room is b in? Who are you? Who is in room x? Supporters will give true, no supporters will give false, and the third type will give at will. Now give the number of three types of people, Now judge whether a can find B, and if so, ask at least a few questions
Idea: if the number of supporters is greater than the sum of the other two categories, obviously a can always find b, because as long as a asks the next person, he must answer really. If the number given is 1,0,0, it means there is only one b, so there is no need to ask
code
#include <bits/stdc++.h>
#define ll long long
#define INF 0x3f3f3f3f
using namespace std;
int a,b,c;
int main() {
cin.tie(0);
ios::sync_with_stdio(0);
cin >>a>>b>>c;
if(a==1&&b==0&&c==0)cout <<"YES\n0";
else if(a>b+c)cout <<"YES\n"<<2*(b+c)+1;
else cout <<"NO";
return 0;
}
J
Main idea of the title: omitted
Train of thought: for the KM template question, you need to pay attention to the structure of the diagram. After the structure, you need to use it O ( n 3 ) O(n^3) O(n3) template for maximum weight perfect matching
code
#include <bits/stdc++.h>
#define int long long
#define inf 0x3f3f3f3f
using namespace std;
const int maxn=512;
int pre[maxn],match[maxn],delta[maxn],graph[maxn][maxn],n,res,l[maxn],r[maxn];
int a[maxn],p[maxn],b[maxn],c[maxn];
bool visl[maxn],visr[maxn];
void maxmatch(int u) {
int x,y=0,d,id=0;
memset(pre,0,sizeof(pre));//pre is used to record the previous edge
for(int i=1; i<=n; i++)delta[i]=inf;//Initialize right point set
match[y]=u;//Initialize matching relationship
while(1) {
x=match[y];
d=inf;//initialization
visr[y]=1;//visit
for(int i=1; i<=n; i++) {
if(visr[i])continue;
if(delta[i]>l[x]+r[i]-graph[x][i]) {//Can you add an edge x-i
delta[i]=l[x]+r[i]-graph[x][i];
pre[i]=y;//Connect an unmatched edge
}
if(delta[i]<d) {//Find a point with the least modification value
d=delta[i];//Record value
id=i;//Record number
}
}
for(int i=0; i<=n; i++)
if(visr[i])l[match[i]]-=d,r[i]+=d;//Try to modify
else delta[i]-=d;//The edge is not the shortest edge and may become the shortest edge after subtraction
y=id;
if(match[y]==-1)break;//Cannot continue matching
}
while(y) {//Construction matching
match[y]=match[pre[y]];
y=pre[y];
}
}
int KM() {
memset(match,-1,sizeof(match));//Empty match
memset(l,0,sizeof(l));
memset(r,0,sizeof(r));
for(int i=1; i<=n; i++) {
memset(visr,0,sizeof(visr));
maxmatch(i);//BFS left point set
}
for(int i=1; i<=n; i++)
if(match[i]!=-1)res+=graph[match[i]][i];
return res;
}
signed main() {
ios::sync_with_stdio(0);
cin.tie(0);
cin >>n;
for(int i=1; i<=n; i++)cin >>a[i];
for(int i=1; i<=n; i++)cin >>p[i];
for(int i=1; i<=n; i++)cin >>b[i];
for(int i=1; i<=n; i++)cin >>c[i];
//Input data
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
for(int k=1; k<=n; k++)
if(b[i]+c[j]>a[k])graph[i][j]+=p[k];//If you can defeat, build an edge
cout <<KM();
return 0;
}
/*
4
1 2 3 4
1 1 1 1
0 0 1 1
0 1 1 2
*/
K
Give a triangle and a point. If the point is not on the boundary, output - 1. If the point is on the boundary, find another point, so that the connecting line between two points can divide the triangle into two parts with equal area
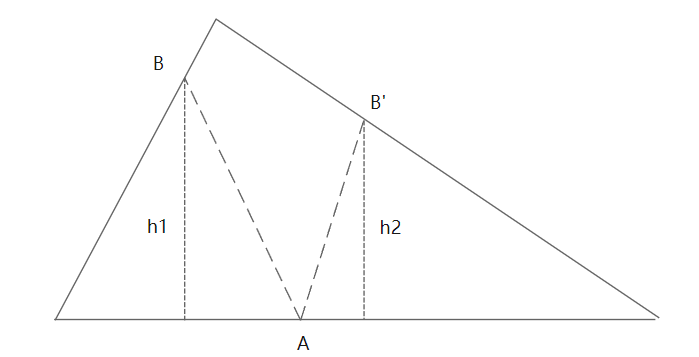
Idea: first judge whether the given point is on the boundary. If it is not, directly output - 1. If it is, try two points on the other two sides to calculate the total triangle area, as shown in the figure. Calculate the height of the triangle that meets the total area / 2 under different conditions, and then calculate the corresponding coordinates according to the height
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const double eps = 1e-10;
int sign(double x)//Symbols for judging floating point numbers
{
if(fabs(x) <= eps) return 0;
if(x > 0) return 1;
else return -1;
}
struct Point
{
double x,y;
Point() {}
//Definition operation
Point(double _x,double _y)
{
x = _x;
y = _y;
}
Point operator + (const Point &b)const
{
return Point(x+b.x,y+b.y);
}
Point operator - (const Point &b)const
{
return Point(x-b.x,y-b.y);
}
Point operator * (const double &k)const //Multiplication constant
{
return Point(x*k,y*k);
}
Point operator / (const double &k)const
{
return Point(x/k,y/k);
}
double len()
{
return x * x + y * y;
}
};
typedef Point Vector;//Define redefines a point as a vector
Point p[4],pp;//Directly predefined variables, p three points, pp one point
double cross(Vector a,Vector b)//Cross product
{
return a.x * b.y - a.y * b.x;
}
double dot(Vector a,Vector b)//Dot product
{
return a.x * b.x + a.y * b.y;
}
double dis(Point a,Point b)//Distance between two points
{
return sqrt((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y));
}
Point answer(int flag)
{
Point ans;
if(flag == 1)
{
double d1 = dis(pp,p[2]);
double d2 = dis(pp,p[3]);
if(fabs(d1 - d2) <= eps)
ans = p[1];
else
{
double rate;
Vector v1,v2,v3;
if(d1 > d2)
{
v1 = pp - p[2],v2 = p[1] - p[2],v3 = p[3] - p[2];
double dd = fabs(cross(v1,v2)) / v2.len();
double hh = fabs(cross(v3,v2)) / v2.len();
rate = hh / dd;
ans = p[2] + (p[1]-p[2]) * 0.5 * rate;
}
else
{
v1 = pp - p[3],v2 = p[1] - p[3],v3 = p[2] - p[3];
double dd = fabs(cross(v1,v2)) / v2.len();
double hh = fabs(cross(v3,v2)) / v2.len();
rate = hh / dd;
ans = p[3] + (p[1]-p[3]) * 0.5 * rate;
}
}
}
else if(flag == 2)
{
double d1 = dis(pp,p[1]);
double d2 = dis(pp,p[3]);
if(fabs(d1 - d2) <= eps)
ans = p[2];
else
{
double rate;
Vector v1,v2,v3;
if(d1 > d2)
{
v1 = pp - p[1],v2 = p[2] - p[1],v3 = p[3] - p[1];
double dd = fabs(cross(v1,v2)) / v2.len();
double hh = fabs(cross(v3,v2)) / v2.len();
rate = hh / dd;
ans = p[1] + (p[2]-p[1]) * 0.5 * rate;
}
else
{
v1 = pp - p[3],v2 = p[2] - p[3],v3 = p[1] - p[3];
double dd = fabs(cross(v1,v2)) / v2.len();
double hh = fabs(cross(v3,v2)) / v2.len();
rate = hh / dd;
ans = p[3] + (p[2]-p[3]) * 0.5 * rate;
}
}
}
else if(flag == 3)
{
double d1 = dis(pp,p[1]);
double d2 = dis(pp,p[2]);
if(fabs(d1 - d2) <= eps)
ans = p[3];
else
{
double rate;
Vector v1,v2,v3;
if(d1 > d2)
{
v1 = pp - p[1],v2 = p[3] - p[1],v3 = p[2] - p[1];
double dd = fabs(cross(v1,v2)) / v2.len();
double hh = fabs(cross(v3,v2)) / v2.len();
rate = hh / dd;
ans = p[1] + (p[3]-p[1]) * 0.5 * rate;
}
else
{
v1 = pp - p[2],v2 = p[3] - p[2],v3 = p[1] - p[2];
double dd = fabs(cross(v1,v2)) / v2.len();
double hh = fabs(cross(v3,v2)) / v2.len();
rate = hh / dd;
ans = p[2] + (p[3]-p[2]) * 0.5 * rate;
}
}
}
return ans;
}
void solve()
{
Point ans;
for(int i = 1; i <= 3; i ++)
scanf("%lf%lf",&p[i].x,&p[i].y);
scanf("%lf%lf",&pp.x,&pp.y);
if(pp.x == p[1].x && pp.y == p[1].y)//Determine whether the fourth point is the endpoint
{
Point mid = (p[2] + p[3]) / 2.0;
printf("%.10f %.10f\n",mid.x,mid.y);
return ;
}
if(pp.x == p[2].x && pp.y == p[2].y)
{
Point mid = (p[1] + p[3]) / 2.0;
printf("%.10f %.10f\n",mid.x,mid.y);
return ;
}
if(pp.x == p[3].x && pp.y == p[3].y)
{
Point mid = (p[1] + p[2]) / 2.0;
printf("%.10f %.10f\n",mid.x,mid.y);
return ;
}
int flag = 0;//Judge whether the fourth point is legal
Vector v1 = pp - p[1],v2 = pp - p[2],v3 = pp - p[3];
if(sign(dot(v1,v2)) == -1 && sign(cross(v1,v2)) == 0) flag = 3;
else if(sign(dot(v1,v3)) == -1 && sign(cross(v1,v3)) == 0) flag = 2;
else if(sign(dot(v2,v3)) == -1 && sign(cross(v2,v3)) == 0) flag = 1;
if(!flag)
{
printf("-1\n");
return ;
}
ans=answer(flag);//flag 1 represents the edge between p2 and p3, 2 represents the edge between p1 and p3, and 3 represents the edge between p1 and p2
printf("%.10f %.10f\n", ans.x, ans.y);
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
solve();
}
return 0;
}