The gardener Xiao Q raised two kinds of flowers, one white flower and one safflower. Now Xiao Q put these flowers on display. When placed, the number of continuous white flowers can only be multiple of K (multiple can be 0), otherwise it will wither. Given A and B now, little Q wants to know how many kinds of pendulum schemes with length [a,b].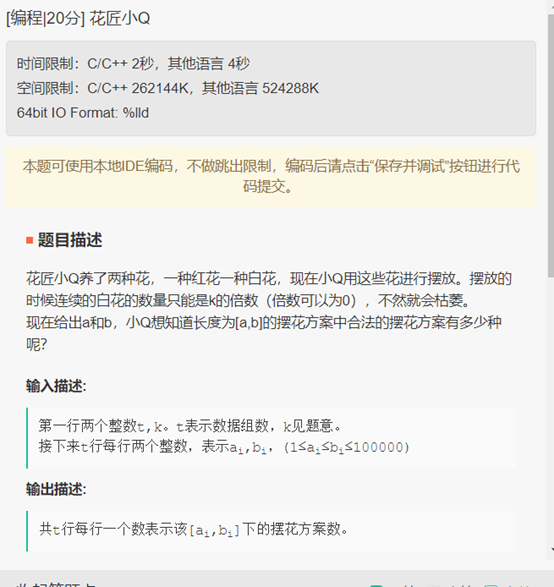


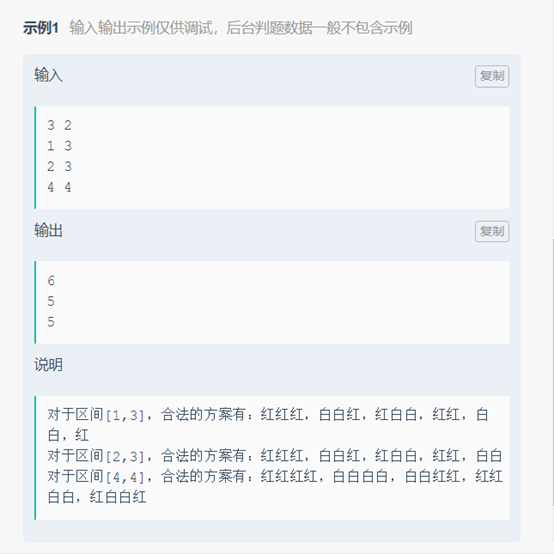
Analysis:
1. Let the current length be X and X belong to [a,b].
2. When X < K, it can only be all safflower, one kind
3. When X=K, it can only be white or safflower.
4. When X > K, the situation needs to be divided.
1. White flowers are 0 * k.
2. White flowers are 1 * k.
3. White flowers are 2*k...
At this time, the k white flowers are regarded as one, and the current problems are simplified as the following examples:

Example: Five pots of safflower and three pots of yellow flower are arranged in a row.
These flowers are the same except for their color.
How many methods are there in the end when yellow flowers are not adjacent to each other?
Interpolation is considered because yellow flowers are not adjacent to each other.
First put the safflower, the safflower grows the same, so no matter how it is placed, there is only one way.
 Because yellow flowers grow the same, so insert yellow flowers into six empty safflower, a total of C3 6=20 methods.

But the white flowers here can be adjacent, so:

Example: Place three pots of safflower and two pots of yellow flowers in a row.
How many methods do these flowers have in common except for their color?
Analysis: Consider the arrangement of repeatable elements.
According to the formula: there are (5!) / (3! 2! = 10 kinds, complete ok
rrrhh   hhrrr  rhrhr   rhrrh
rrhrh   hrhrr  rrhhr   hrrhr
rhhrr   hrrrh

Next, it's easy to write code:
I wrote the output of the process for easy understanding.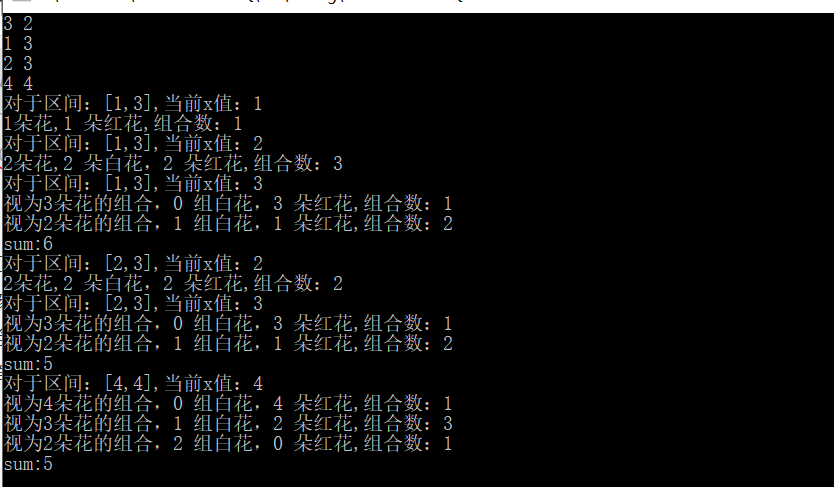

#include <stdio.h>
#include <stdlib.h>

int calculateN(int num)
{
    int i=1;
    int calcu=1;
    do
    {
        calcu*=i;
        i++;
    }
    while(i<=num);
    //printf("%d n!=%d\n",num,calcu);
        return calcu;
}

int main()
{
    int t=0;
    int k=0;
    scanf("%d %d",&t,&k);
    int flowerlength[2000][2];
    int i=0;
    for(i=0; i<t; i++)
    {
        scanf("%d %d",&flowerlength[i][0],&flowerlength[i][1]);
    }

    for(i=0; i<t; i++)
    {
        int x=0;
        int sum=0;
        for(x=flowerlength[i][0]; x<=flowerlength[i][1]; x++)
        {
            printf("For intervals:[%d,%d],current x Value:%d\n",flowerlength[i][0],flowerlength[i][1],x);
            if(x<k)
            {
                sum+=1;
                 printf("%d A flower,%d Flos Carthamus,Combination number:%d\n",x,x,sum);
            }
            else if(x==k)
            {sum+=2;
                 printf("%d A flower,%d White flower,%d Flos Carthamus,Combination number:%d\n",x,x,x,sum);

            }
            else if(x>k)
            {
                int n=0;//Limit the number of white flowers
                while(n*k<=x)
                {
                    int cal=calculateN(n+x-n*k)/(calculateN(n)*calculateN(x-n*k));
                    sum+=cal;
                    printf("Regard as%d The combination of flowers,%d Group of white flowers,%d Flos Carthamus,Combination number:%d\n",n+x-n*k,n,x-n*k,cal);
                    n+=1;
                }
            }
            else
            {
                printf("error!\n");
            }

        }
        printf("sum:%d\n",sum);

    }

    return 0;
}