Critical path:
Planning, construction process, production process and procedure process are usually regarded as a project. The project is usually divided into several sub projects called "activities". After these "activities" are completed, the project can be completed. AOE net is usually used to represent engineering. AOE net is a weighted directed acyclic graph, in which the vertex represents the EVENT, the arc represents the activity, and the weight represents the duration of the activity. AOE net can be used to estimate the completion time of the project. It can make people understand:
(1) How much time does it take to study a project?
(2) What are the key activities affecting the project progress?
Because some activities in AOE network can be carried out in parallel, from the start point to each vertex, there may be more than one directed path from the start point to the completion point, and the length of these paths may also be different. Although the time required to complete the activities of different paths is different, the project is completed only when all the activities on each path are completed. Therefore, the shortest time required to complete the project is the length of the longest path from the start point to the completion point, that is, the sum of the durations of all activities on this path The length of this path is called critical path.
Example: AOE diagram is as follows:
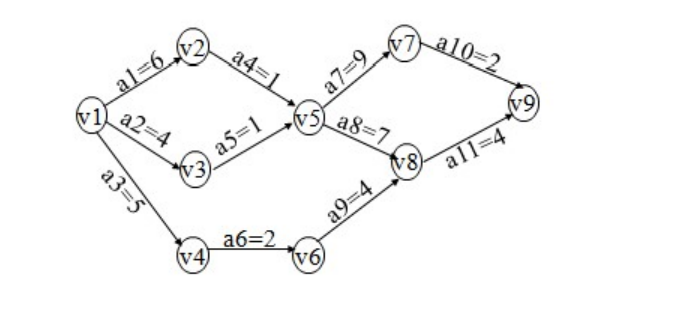
After the program is executed, it should output:
Key activities: A1, a4, a7, a10, a8, a11
The critical paths are: A1 - > A4 - > A7 - > A10 (or V1 - > V2 - > V5 - > V7 - > V9) and A1 - > A4 - > A8 - > a11 (or V1 - > V2 - > V5 - > V8 - > V9)
The time spent is at least: 18 (time units).
Algorithm design:
1. Use adjacency table to store a weighted directed graph.
2. The graph is topologically sorted, and the earliest occurrence time Ve[i] of events is calculated.
3. According to the sorting result, judge whether there is a directed ring in the graph.
4. Calculate the latest occurrence time Vl[i] of the event according to the inverse topology sequence.
5. Calculate the earliest and latest occurrence time of activities, judge key activities and find out key paths.
flow chart:

Algorithm implementation:
#include<bits/stdc++.h>
using namespace std;
typedef int Status;
typedef int Boolean;
#define TRUE 1
#define FALSE 0
#define OK 1
#define ERROR 0
#define MAX_NAME 5
typedef int InfoType;
typedef char VertexType[MAX_NAME];
/* --------------------------------- Adjacency table storage representation of graph--------------------------------*/
#define MAX_VERTEX_NUM 20
typedef struct ArcNode{ //Table node
int adjvex; //The subscript of the vertex to which the arc points
struct ArcNode *nextarc; //Pointer to the next arc
InfoType *info; //Edge weight
}ArcNode;
typedef struct{
VertexType data; //Vertex information
ArcNode *firstarc; //The address of the first table node, a pointer to the first arc attached to the vertex
}VNode, AdjList[MAX_VERTEX_NUM];//Adjacency table
typedef struct{ //chart
AdjList vertices;
int vexnum, arcnum; //Number of vertices and edges
int kind; //Types of Graphs
}ALGraph;
/* ----------------------------- The adjacency table of the graph needs to be used to store the basic operations--------------------------*/
int LocateVex(ALGraph G, VertexType u){
//If there is vertex u in G, the position of the vertex in the graph is returned; Otherwise - 1 is returned
int i;
for (i = 0; i < G.vexnum; ++i)
if (strcmp(u, G.vertices[i].data) == 0)
return i;
return -1;
}
Status CreateGraph(ALGraph &G){ //Create directed net
int i, j, k;
int w; // Weight
VertexType va, vb;
ArcNode *p;
G.kind = 1;//Directed net
printf("Please enter the number of vertices and edges of the graph(Space separated): ");
scanf("%d%d", &G.vexnum, &G.arcnum);
printf("Please enter%d The value of the first vertex(<%d Characters):\n", G.vexnum, MAX_NAME);
for (i = 0; i < G.vexnum; ++i) {
scanf("%s", G.vertices[i].data);
G.vertices[i].firstarc = NULL;
}
printf("Please enter each arc in sequence(edge)Weight, arc tail and arc head(Space):\n");
for (k = 0; k < G.arcnum; ++k) {
scanf("%d%s%s", &w, va, vb);
i = LocateVex(G, va); // Arc tail
j = LocateVex(G, vb); // Arc head
p = (ArcNode*)malloc(sizeof(ArcNode));
p->adjvex = j;
p->info = (int *)malloc(sizeof(int));
*(p->info) = w;
p->nextarc = G.vertices[i].firstarc; // Insert in header
G.vertices[i].firstarc = p;
}
return OK;
}
void Display(ALGraph G){ // Adjacency table G of output graph
int i;
ArcNode *p;
printf("Directed graph\n");
printf("%d Vertices:\n", G.vexnum);
for (i = 0; i < G.vexnum; ++i)
printf("%s ", G.vertices[i].data);
printf("\n%d Strip arc(edge):\n", G.arcnum);
for (i = 0; i < G.vexnum; i++){
p = G.vertices[i].firstarc;
while (p){
printf("%s→%s :%d", G.vertices[i].data, G.vertices[p->adjvex].data, *(p->info));
p = p->nextarc;
}
printf("\n");
}
}
void FindInDegree(ALGraph G, int indegree[]){ // Find the penetration of vertices
int i;
ArcNode *p;
for (i = 0; i < G.vexnum; i++)
indegree[i] = 0; /* Initial value assignment */
for (i = 0; i < G.vexnum; i++){
p = G.vertices[i].firstarc;
while (p){
indegree[p->adjvex]++;
p = p->nextarc;
}
}
}
typedef int SElemType;
/* ----------------------------------- Sequential storage representation of stack-----------------------------------*/
#define STACK_INIT_SIZE 10
#define STACKINCREMENT 2
typedef struct SqStack{
SElemType *base;
SElemType *top;
int stacksize;
}SqStack;
Status InitStack(SqStack &S){
S.base = (SElemType *)malloc(STACK_INIT_SIZE * sizeof(SElemType));
if (!S.base)
exit(_OVERFLOW);
S.top = S.base;
S.stacksize = STACK_INIT_SIZE;
return OK;
}
Status StackEmpty(SqStack S){
if (S.top == S.base)
return TRUE;
else
return FALSE;
}
Status GetTop(SqStack s,SElemType &e){
if(s.base==s.top)
return 0;
e = *(s.top - 1);
return 1;
}
Status Push(SqStack &S, SElemType e){
if (S.top - S.base >= S.stacksize) {
S.base = (SElemType *)realloc(S.base, (S.stacksize + STACKINCREMENT) * sizeof(SElemType));
if (!S.base)
exit(_OVERFLOW);
S.top = S.base + S.stacksize;
S.stacksize += STACKINCREMENT;
}
*(S.top)++ = e;
return OK;
}
Status Pop(SqStack &S, SElemType &e){ /* If the stack is not empty, delete the top element of S, return its value with e, and return OK; Otherwise, ERROR is returned */
if (S.top == S.base)
return ERROR;
e = *--S.top;
return OK;
}
int ve[MAX_VERTEX_NUM], vl[MAX_VERTEX_NUM];//e []: earliest occurrence time vl []: latest occurrence time
bool flag = 0;
vector<string> path;
int top,down;
void dfs(ALGraph G, int u){
if (G.vertices[u].data == G.vertices[top].data) {//Search to end
if (flag) cout << "\n Or:\n";
cout << G.vertices[down].data; //Output starting point
for(auto &it:path) //Traverse output critical path
cout << it;
flag = 1;
return;
}
ArcNode* p = G.vertices[u].firstarc; //Initial edge
for (; p; p = p->nextarc) { //ergodic
int k = p->adjvex; //The subscript of the vertex to which the arc points
int dut = *(p->info); //Weight of arc
if (ve[u] == vl[k] - dut) { //This is a key activity
path.push_back("->");
path.push_back(G.vertices[k].data); //Record key activities
dfs(G, k); //Key activities to continue DFS search for the next node
path.pop_back(); //to flash back
path.pop_back(); //to flash back
}
}
}
//Algorithm 7.13
Status TopologicalOrder(ALGraph G, SqStack &T){
int j, k, count, indegree[MAX_VERTEX_NUM],e;
SqStack S;
ArcNode *p;
FindInDegree(G, indegree);
InitStack(S);
for (j = 0; j < G.vexnum; ++j)
if (!indegree[j])
Push(S, j);
GetTop(S, down); //Record start position
InitStack(T);
count = 0;
for (j = 0; j < G.vexnum; ++j)
ve[j] = 0; //initialization
while (!StackEmpty(S)){
Pop(S, j);
Push(T, j);
++count; //Number of vertices stacked
for (p = G.vertices[j].firstarc; p; p = p->nextarc){ //Traversal adjacency table
k = p->adjvex; //The subscript of the vertex to which the arc points
if (--indegree[k] == 0) //Reduce the input to zero and put it on the stack
Push(S, k);
if (ve[j] + *(p->info) > ve[k])//Topology positive order update max
ve[k] = ve[j] + *(p->info);
}
}
if (count < G.vexnum){
printf("This directed network has a loop\n");
return ERROR;
}
else{
GetTop(T, top);//The last node of topology sorting is the end point
return OK;
}
}
//Algorithm 7.14
Status CriticalPath(ALGraph G){
SqStack T;
int i, j, k, ee, el;
ArcNode *p;
char dut, tag;
if (!TopologicalOrder(G, T)) // Generate a directed ring
return ERROR;
j = ve[0];
for (i = 1; i < G.vexnum; i++) //J = value of max (VE []) completion point
if (ve[i] > j)
j = ve[i];
int maxn = j;
for (i = 0; i < G.vexnum; i++) // The latest (maximum) occurrence time of the initialization vertex event
vl[i] = j; // Earliest occurrence time of completion point
while (!StackEmpty(T)) // Find the vl value of each vertex in topological reverse order
for (Pop(T, j), p = G.vertices[j].firstarc; p; p = p->nextarc){
k = p->adjvex;
dut = *(p->info); // dut<j,k>
if (vl[k] - dut < vl[j])
vl[j] = vl[k] - dut;
}
printf(" j k dut ee el tag\n");
for (j = 0; j < G.vexnum; ++j)//Seeking ee,el and key activities
for (p = G.vertices[j].firstarc; p; p = p->nextarc){
k = p->adjvex;
dut = *(p->info);//Edge weight
ee = ve[j];
el = vl[k] - dut;
tag = (ee == el) ? '*' : ' ';
printf("%2d %2d %3d %3d %3d %c\n", j, k, dut, ee, el, tag);
}
printf("Key activities are:\n");
for (j = 0; j < G.vexnum; ++j)
for (p = G.vertices[j].firstarc; p; p = p->nextarc){
k = p->adjvex;
dut = *(p->info);
if (ve[j] == vl[k] - dut)
printf("%s→%s\n", G.vertices[j].data, G.vertices[k].data); // Output key activities
}
printf("The critical path is:\n");
dfs(G,0);
printf("\n The minimum time spent is:%d\n", maxn);
return OK;
}
int main(){
ALGraph h;
CreateGraph(h);
Display(h);
CriticalPath(h);
}
Test example:

Add two more:
V1 - > V10 (weight 8)
V10 - > V9 (weight is 10)
Test data:
Please enter the number of vertices and edges of the graph(Space separated): 10 13 Please enter a value for 10 vertices(<5 Characters): v1 v2 v3 v4 v5 v6 v7 v8 v9 v10 Please enter each arc in sequence(edge)Weight, arc tail and arc head(Space): 6 v1 v2 4 v1 v3 5 v1 v4 1 v2 v5 1 v3 v5 2 v4 v6 9 v5 v7 7 v5 v8 4 v6 v8 2 v7 v9 4 v8 v9 8 v1 v10 10 v10 v9
Operation results
Directed graph 10 Vertices: v1 v2 v3 v4 v5 v6 v7 v8 v9 v10 13 Strip arc(edge): v1→v10 :8v1→v4 :5v1→v3 :4v1→v2 :6 v2→v5 :1 v3→v5 :1 v4→v6 :2 v5→v8 :7v5→v7 :9 v6→v8 :4 v7→v9 :2 v8→v9 :4 v10→v9 :10 j k dut ee el tag 0 9 8 0 0 * 0 3 5 0 3 0 2 4 0 2 0 1 6 0 0 * 1 4 1 6 6 * 2 4 1 4 6 3 5 2 5 8 4 7 7 7 7 * 4 6 9 7 7 * 5 7 4 7 10 6 8 2 16 16 * 7 8 4 14 14 * 9 8 10 8 8 * Key activities are: v1→v10 v1→v2 v2→v5 v5→v8 v5→v7 v7→v9 v8→v9 v10→v9 The critical path is: v1->v10->v9 Or: v1->v2->v5->v8->v9 Or: v1->v2->v5->v7->v9 Minimum time spent: 18
experience
- In the process of using the adjacency list to save the map, get familiar with the related operations of the linked list again.
- Review the writing and use of stack. The topological sequence is solved by stack.
- When conducting topological sorting, master the calculation of node degree (in degree) and learn the application of topological order: use topological sorting to calculate the earliest occurrence time.
- Review the writing and use of stack. The topological order sequence is stored on the stack, and the topological reverse order sequence is obtained when it is out of the stack. The calculation of the latest occurrence time is solved by topological reverse order.
- Review the depth first search on the map. Use DFS to output critical paths.
reference
[1] Yan Weimin, WU Weimin Data structure (C language version) [M]. Beijing: Tsinghua University Press, April 1997