2021 12th Lanqiao cup provincial tournament group B C/C++
preface:
Recall that I participated in the blue bridge cup for the first time last year. At that time, I was a freshman and full of enthusiasm. Although I only learned c language and had only a little contact with c + +, I signed up for the competition at the suggestion of my senior. They all say that this violence cup is very simple to mix a provincial award. On the field, I called the good guy directly. The Dev I gave was in English. What if I didn't know the words? This is a human thing. The program has been running for more than half an hour, but it hasn't finished yet. It's too violent... I only deserve to experience the most expensive milk and bread 😭
Question A: Space
-
[problem description]
Xiaolan is going to use 256 MB of memory space to open an array. Each element of the array is a 32-bit binary integer. If the space occupied by the program and the auxiliary space required to maintain memory are not considered, how many 32-bit binary integers can be stored in 256 MB of space? -
[answer submission]
This is a question filled in with results. You just need to calculate the results and submit them. The result of this question is an integer. When submitting the answer, only fill in this integer. If you fill in the redundant content, you will not be able to score.
answer
1 B = 8 bit
1 KB = 1024 B
1 MB = 1024 KB
1 GB = 1024 MB
1 TB = 1024 GB
Byte, byte, B, these words are equivalent, 1 Byte=8 bit;
Bit, bit, bit, b, these words are equivalent. A bit (that is, 1 bit) is a binary number
A 32-bit binary integer takes up 4 bytes.
The answer is:
256 * 1024 * 1024 / 4 = 67,108,864
Or 256 * 1024 * 1024 * 8 / 32 = 67108864
answer
67108864
Question B: card
-
[problem description]
Xiaolan has many digital cards, each with numbers 0 to 9.
Xiaolan is going to use these cards to spell some numbers. He wants to spell positive integers from 1. Each time he spell one, he will save it. The card can't be used to spell other numbers.
Xiaolan wants to know how much she can spell from 1.
For example, when Xiaolan has 30 cards, including 3 cards from 0 to 9, Xiaolan can spell 1 to 10, but when spell 11, there is only one card 1, which is not enough to spell 11.
Now Xiaolan has 2021 cards from 0 to 9, a total of 20210. How many can Xiaolan spell from 1?
Tip: it is recommended to use computer programming to solve the problem. -
[answer submission]
This is a question filled in with results. You just need to calculate the results and submit them. The result of this question is an integer. When submitting the answer, only fill in this integer. If you fill in the redundant content, you will not be able to score.
answer
Violence is over!
#include <bits/stdc++.h>
using namespace std;
int main() {
vector<int> array(10, 2021);
for (int i = 1; ; i++) {
int t = i;
while (t) {
int a = t % 10;
if (array[a] > 0) {
array[a]--;
} else {
break;
}
t /= 10;
}
if (t) {
cout<<i<<endl;
break;
}
}
return 0;
}
The operation result here is 3182;
Note: here is exactly 3182. This number cannot be spelled. So the result is minus one.
answer
3181
Pay attention to the examination! Pay attention to the examination!! Pay attention to the examination!!! I just fell into this pit 😭
Question C: straight line
- [problem description]
In the plane rectangular coordinate system, two points can determine a straight line. If there are multiple points on a straight line, the straight line determined by any two of these points is the same.
2 on a given plane × Three integer points {(x, y) | 0 ≤ x < 2, 0 ≤ y < 3, X ∈ Z, y ∈ Z)}, i.e. points where the abscissa is an integer between 0 and 1 (including 0 and 1) and the ordinate is an integer between 0 and 2 (including 0 and 2). These points determine a total of 11 different lines.
20 on a given plane × 21 whole points {(x,y)0 ≤ x < 20,0 ≤ y < 21, X ∈ Z,y ∈ Z}, that is, the abscissa is О To 19 (inclusive) О The integer and ordinate between and 19) are О To 20 (inclusive) О And 20). How many different straight lines are determined by these points. - [answer submission]
This is a question filled in with results. You just need to calculate the results and submit them. The result of this question is an integer. When submitting the answer, only fill in this integer. If you fill in the redundant content, you will not be able to score.
answer
From example: 2 × Three integral points {(x, y) | 0 ≤ x < 2, 0 ≤ y < 3, X ∈ Z, y ∈ Z)}, 11 different straight lines can be determined.
(there are few points, so you can draw pictures to verify)
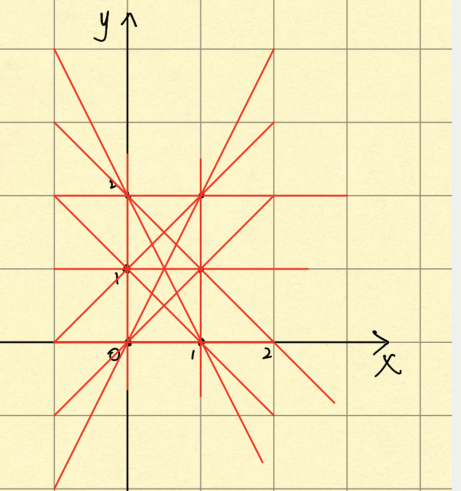
twenty × 21 whole points {(x,y)0 ≤ x < 20,0 ≤ y < 21, X ∈ Z,y ∈ Z} are realized by programming.
Idea:
Two points determine a straight line. For multiple straight lines, the final number of straight lines can be obtained by removing the weight of intercept and slope.
Pit!!! 😶
The calculation results of slope and intercept are decimal, which may affect the de duplication due to insufficient accuracy.
Solution
The slope and intercept are expressed in fractions, which can avoid the impact of accuracy!
#include <bits/stdc++.h>
using namespace std;
int gcd(int a, int b) { //Calculate the greatest common divisor of two numbers
int t;
if (a < b) {
t = b;
b = a;
a = t;
}
while (b) {
t = a % b;
a = b;
b = t;
}
return a;
}
int main(){
vector<pair<int,int>> array; // Store 20 * 21 points
set<pair<pair<int, int>, pair<int, int>>> line; // Store the slope and intercept of each line (with weight removal effect)
for (int i = 0; i < 20; i++) {
for (int j = 0; j < 21; j++) {
array.push_back(make_pair(i,j));
}
}
int n = array.size();
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
int x1 = array[i].first, y1 = array[i].second;
int x2 = array[j].first, y2 = array[j].second;
if (x1 == x2 || y1 == y2) { //Lines parallel to the coordinate axis are considered separately
continue;
} else {
int t;
double k1 = y2 - y1; //Slope molecule
double k2 = x2 - x1; //Denominator of slope
t = gcd(abs(k1), abs(k2));
if (k1 * k2 > 0) { //Reductive differentiation
k1 /= t;
k2 /= t;
} else{ //If the slope is negative, the minus sign goes to the molecule
k1 = -abs(k1 / t);
k2 = abs(k2 / t);
}
double b1 = y1 * x2 - x1 * y2; //Intercept molecule
double b2 = x2 - x1; //Denominator of intercept
t = gcd(abs(b1), abs(b2));
if (b1 * b2 > 0) { //Reductive differentiation
b1 /= t;
b2 /= t;
} else{ //If the intercept is negative, the minus sign is stored on the molecule
b1 = -abs(b1 / t);
b2 = abs(b2 / t);
}
pair<int, int>p1 = make_pair(k1, k2);
pair<int, int>p2 = make_pair(b1, b2);
pair<pair<int, int>, pair<int, int>> p = make_pair(p1, p2); //Save set de duplication
line.insert(p);
}
}
}
//The result adds 21 lines parallel to the x-axis and 20 lines parallel to the y-axis
cout<<line.size() + 20 + 21;
return 0;
}
answer
40257
Question D: goods placement
-
[problem description]
Xiaolan has a large warehouse, which can put a lot of goods.
Now, Xiaolan has n boxes of goods to be placed in the warehouse, and each box of goods is a regular cube. Xiaolan stipulates three mutually perpendicular directions of length, width and height. The side of each box of goods must be strictly parallel to the length, width and height.
Xiaolan hopes that all the goods will eventually be placed into a big cube. That is, pile L, W and H goods respectively in the direction of length, width and height, meeting the requirement of n = L x W × H.
Given n, how many schemes for stacking goods meet the requirements.
For example, when n = 4, there are six schemes: 1 × one × 4,1 × two × 2,1 × four × 1,2 × one × 2,2 × two × 1,4 × one × 1.
How many schemes are there when n = 2021041820210418 (note that there are 16 digits)?
Tip: it is recommended to use computer programming to solve the problem. -
[answer submission]
This is a question filled in with results. You just need to calculate the results and submit them. The result of this question is an integer. When submitting the answer, only fill in this integer. If you fill in the redundant content, you will not be able to score.
answer
The general idea is to factorize n.
Therefore, the most direct thought is this violent solution.
#include <bits/stdc++.h>
using namespace std;
int main(){
long long n = 2021041820210418;
long long ans = 0;
for (long long i = 1; i <= n; i++) {
if (n % i == 0) {
for (long long j = 1; j <= n / i; j++) {
if (n / i % j == 0) {
ans++;
}
}
}
}
cout<<ans<<endl;
return 0;
}
The result is that the amount of data is too large to calculate the result after a long time! 🤣
Simple optimization:
Find out a group of decomposition methods and calculate the other results directly according to the arrangement and combination, which can reduce the dimension of decomposition factor.
#include <bits/stdc++.h>
using namespace std;
int main(){
long long n = 2021041820210418;
long long ans = 0;
for (long long i = 1; i * i * i <= n; i++) {
if (n % i == 0) {
for (long long j = i; i * j * j <= n; j++) {
if (n / i % j == 0) {
long long t = n / i / j;
if (i == j && j == t) { //All three numbers are the same
ans++;
} else if (i == j || i == t || j == t) { //Two of the three numbers are the same
ans += 3;
} else { //The three numbers are different
ans += 6;
}
}
}
}
}
cout<<ans<<endl;
return 0;
}
answer
2430
Another idea:
First find out all the factors of n (the number of factors is relatively small, which is convenient for enumeration), and then cite the case where the product of the three factors is equal to n.
Question E: Path
-
[problem description]
Xiaolan is very happy after learning the shortest path. He defines a special graph and hopes to find the shortest path in the graph.
The diagram of Xiaolan consists of 2021 nodes, numbered from 1 to 2021.
For two different nodes a and b, if the absolute value of the difference between a and b is greater than 21, there is no edge connection between the two nodes; If the absolute value of the difference between a and b is less than or equal to 21, there is an undirected edge with a length of the least common multiple of a and b.
For example, there is no edge connection between node 1 and node 23; There is an undirected edge between node 3 and node 24, with a length of 24; There is an undirected edge between node 15 and node 25, with a length of 75.
Please calculate the shortest path length between node 1 and node 2021.
Tip: it is recommended to use computer programming to solve the problem. -
[answer submission]
This is a question filled in with results. You just need to calculate the results and submit them. The result of this question is an integer. When submitting the answer, only fill in this integer. If you fill in the redundant content, you will not be able to score.
answer
The idea of dynamic programming + the solution of violence
#include <bits/stdc++.h>
using namespace std;
long long gcd(long long a, long long b) { //Calculate the greatest common divisor of two numbers
int t;
if (a < b) {
t = b;
b = a;
a = t;
}
while (b) {
t = a % b;
a = b;
b = t;
}
return a;
}
int main(){
vector<vector<long long>> array(2022, vector<long long>(2022, INT_MAX));
for (long long i = 1; i <= 2021; i++) { //Calculate the distance between points directly connected by edges
for (long long j = i + 1; j <= i + 21; j++) {
array[i][j] = i * j / gcd(i, j);
}
}
for (long long i = 1; i <= 2021; i++) {
for (long long j = i + 1; j <= 2021; j++) {
for (long long k = i + 1; k < j; k++) { //Calculate the shortest distance between two points
array[i][j] = fmin(array[i][j], (array[i][k] + array[k][j]));
}
}
}
cout<<array[1][2021]<<endl;
return 0;
}
answer
10266837
Question F: time display
Time limit: 1.0 s memory limit: 256.0 MB
-
[problem description]
Xiaolan wants to cooperate with her friends to develop a time display website. On the server, the friend has obtained the current time, which is expressed as an integer. The value is the number of milliseconds from 00:00:00 on January 1, 1970 to the current time.
Now, Xiaolan will display this time on the client. Xiaolan doesn't need to display the year, month and day. It only needs to display the hours, minutes and seconds, and milliseconds. It can be directly rounded off.
Given a time expressed as an integer, please output the hour, minute and second corresponding to this time. -
[input format]
The input line contains an integer representing the time.
-
[output format]
Output the current time represented by hour, minute and second. The format is HH:MM:SS, where HH represents hour, the value is 0 to 23, MM represents minute, the value is 0 to 59, SS represents second, and the value is 0 to 59. When the hour, minute and second are less than two digits, the leading 0 shall be supplemented.
-
[example input 1]
46800999
-
[sample output 1]
13:00:00
-
[example input 2]
1618708103123
-
[sample output 2]
01:08:23
-
[evaluation case scale and agreement]
For all evaluation cases, the given time is a positive integer no more than 1018.
answer
Simple simulation!
#include <bits/stdc++.h>
using namespace std;
int main(){
long long time;
int hh, mm, ss;
cin>>time;
time /= 1000; //Millisecond to second
time %= 86400; //Convert to time of day
hh = time / 3600;
time -= hh * 3600;
mm = time / 60;
ss = time - mm * 60;
printf("%02d:%02d:%02d",hh, mm, ss);
return 0;
}
Test question G: weight weighing
Time limit: 1.0 s memory limit: 256.0 MB
- [problem description]
You have a balance and N weights. The weights of these n weights are W1, W2,..., WN in turn.
Please calculate how many different weights you can weigh?
Note that the weight can be placed on both sides of the balance.
-
[input format]
The first line of input contains an integer N.
The second line contains N integers: W1, W2,..., WN. -
[output format]
Output an integer representing the answer.
-
[sample input]
3 1 4 6
-
[sample output]
10
-
[example description]
The 10 weights that can be weighed are: 1, 2, 3, 4, 5, 6, 7, 9, 10 and 11.
1 = 1
2 = 6 - 4 (put 6 on one side and 4 on the other side of the balance);
3 = 4 - 1:
4 = 4
5 = 6 - 1
6 = 6
7 = 1 + 6
9 = 4 + 6 - 1
10 = 4 + 6
11 = 1 + 4 + 6
-
[evaluation case scale and agreement]
For 50% of the evaluation cases, 1 < n ≤ 15.
For all evaluation cases, 1 ≤ n ≤ 100, and the total weight of N weights shall not exceed 100000.
answer
01 knapsack idea, dynamic programming solution.
Idea:
- It can be seen from the question that the weight weighed by the weight is a positive integer.
- For each weight, we have three options:
- ① Not selected
- ② Take a negative number (put it on the left of the weight plate)
- ③ Take a positive number (put it on the right side of the weight plate).
-
Here, dp[i][j] is used, I indicates the selection from the previous I weights, and j indicates that the weight of the weighed weight is J.
-
When dp[i][j] is true, it means that the weight of j can be weighed by selecting from the previous I weights;
-
When dp[i][j] is false, it means that the weight of j cannot be weighed after selecting from the previous I weights.
-
Since the total weight of N weights does not exceed 100000. Finally, only traverse dp[i][sum], (I ∈ [1,n], n represents the number of weights; sum represents the total weight of N weights), and the number of true is the total weight that can be weighed.
#include<bits/stdc++.h>
using namespace std;
const int N = 110, M = 200010;
int main() {
int n;
int sum = 0; //Total weight of all weights
vector<int>w(N); //Record the weight of each weight
vector<vector<bool> > dp(N, vector<bool>(M,false)); //Indicates the status of the recorded weight
scanf("%d", &n); //Read in weights
for (int i = 1; i <= n; i++) {
scanf("%d", &w[i]); //Read in the weight of each weight
sum += w[i];
}
dp[0][0] = true; //Initial state setting indicates that the weight is 0 and the state is true
for (int i = 1; i <= n; i++) { //Select from the previous i weights
for (int j = 0; j <= sum; j++) { //The weight to be expressed is j
//If one of the three states is true, the current state is true; Otherwise, it is false
//All weights weighed are positive (conversion required)
dp[i][j] = dp[i - 1][j] || dp[i - 1][fabs(j - w[i])] || dp[i - 1][j + w[i]];
}
}
long long ans = 0;
for (int i = 1; i <= sum; i++) {
if (dp[n][i]) { //Select from n weights to judge whether the weight i can be weighed and counted.
ans++;
}
}
cout<<ans<<endl;
return 0;
}
Question H: Yang Hui triangle
Time limit: 1.0 s memory limit: 256.0 MB
-
[problem description]
The following figure is the famous Yang Hui triangle:
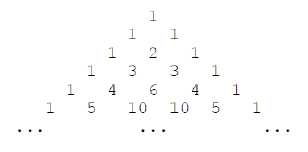
If we arrange all numbers in a row from top to bottom and from left to right, we can get the following sequence:
1,1,1,1,2,1,1,3,3,1,1,4,6,4,1,...
Given a positive integer n, what number is the first occurrence of N in the output sequence?
-
[input format]
Enter an integer N.
-
[output format]
Output an integer representing the answer.
-
[sample input]
6
- [sample output]
13
- [evaluation case scale and agreement]
For 20% of the evaluation cases, 1 ≤ N ≤ 10;
For all evaluation cases, 1 ≤ N ≤ 1000000000.
answer
When I first read the title, I thought it was violence. But, when you see the range of N, you know that violence should be cool~
Violent thinking:
#include<bits/stdc++.h>
using namespace std;
const int N = 8000;
int main() {
int n;
cin>>n;
vector<vector<int> > array(N,vector<int>(N));
for (int i = 0; i < N; i++) {
array[i][i] = array[i][0] = 1;
}
for (int i = 2; i < N; i++) {
for (int j = 1; j <= i; j++) {
array[i][j] = array[i - 1][j] + array[i - 1][j - 1];
}
}
cout<<array[N - 1][N / 2]<<endl;
long long ans = 1;
for (int i = 0; i < N; i++) {
for (int j = 0; j <= i; j++) {
if (array[i][j] == n) {
cout<<ans<<endl;
return 0;
}else {
ans++;
}
}
}
return 0;
}
Question:
- The open capacity is small and can not reach the data range of N;
- The open capacity is large, and the memory exceeds the limit;
Optimize:
Probably more than half of them.
#include<bits/stdc++.h>
using namespace std;
int main(){
long long ans = 1;
long long a[200000];
long long count = 1;
long long n;
cin>>n;
if (n == 1) {
cout<<"1"<<endl;
return 0;
}
for (int i = 1; i < 1000000; i++) { //Number of traversal rows
a[0] = a[i] = 1;
ans++;
for (count = i - 1; count > 0; count--) { //The current row of data takes advantage of symmetry
ans++;
a[count] = a[count] + a[count-1];
if (a[count] == n) { //Find n, output directly and end
cout<<ans<<endl;
return 0;
}
}
ans++;
}
return 0;
}
Question:
- Array a is used to store the data of each row, realizing the reuse of space, but it timed out. 😣😫
Positive solution: find the law + dichotomy
Idea:
- Each value of Yanghui triangle corresponds to the value of permutation and combination.
- Represented by C(r,k), r is the number of rows and k is the number of current rows. (numbering from 0)
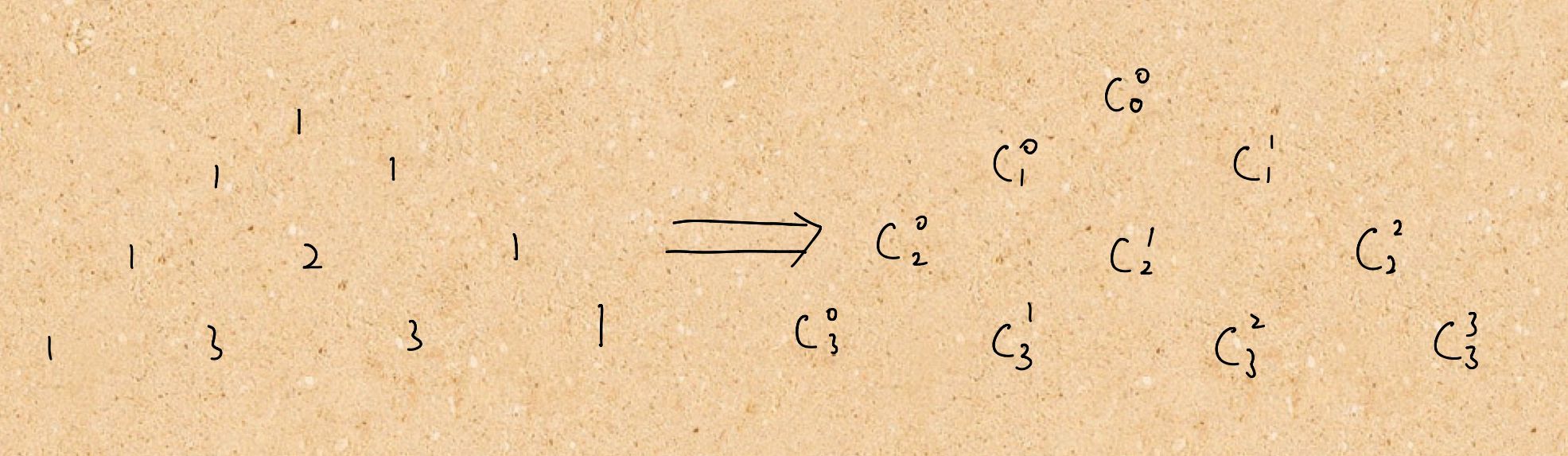
- Yang Hui triangle has symmetry
- (C(a, b) == C(a, a-b)), and the title requires to appear for the first time, so it must be on the left and can be deleted directly on the right!
- Looking at only half of it, each oblique line is monotonic (monotonic increasing except for the outermost oblique line)
- Each diagonal line increases from top to bottom
- Each row decreases from the middle to both sides
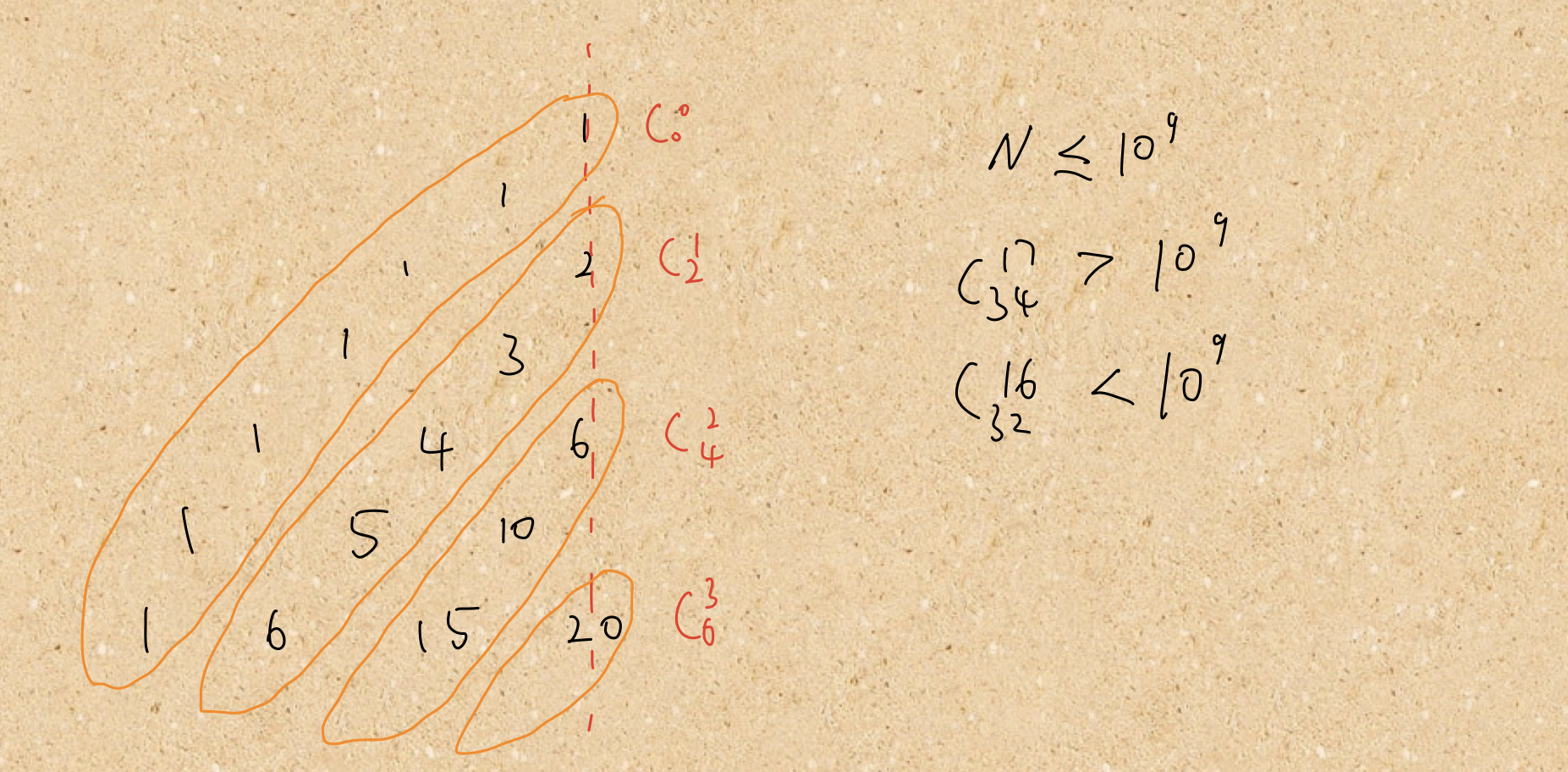
From n < = 109, it can be seen that the Yanghui triangle takes 16 oblique rows at most.
#include<bits/stdc++.h>
using namespace std;
int n;
long long C(int a, int b) { //Find the number of permutations and combinations
long long res = 1;
for (int i = a, j = 1; j <= b; i--, j++) {
res = res * i / j;
// Greater than n is meaningless to prevent explosion of long long
if (res > n) {
return res;
}
}
return res;
}
bool check(int k) {
// Bisect the oblique line and find the first number greater than or equal to n
long long l = k * 2;
long long r = fmax(l,n); // The right endpoint must be larger than the left endpoint
while (l < r) {
long long mid = l + r >> 1;
if (C(mid, k) >= n) {
r = mid;
} else {
l = mid + 1;
}
}
if (C(r, k) != n) {
return false;
}
// Find the number of output
cout<<r * (r + 1) / 2 + k + 1<<endl;
return true;
}
int main(){
cin>>n;
for (int k = 16; ; k--) { //The solution must be found in 16 oblique rows.
if (check(k)) { //Find results
break;
}
}
return 0;
}
Question I: bidirectional sorting
Time limit: 1.0 s memory limit: 256.0 MB
-
[problem description]
Given sequence (a1,a2,..., an) = (1,2,..., n), i.e. ai = i.
Xiaolan will perform m operations on this sequence. Each time, it may arrange a1, a2,..., aqi in descending order, or aqi, aqi+1,..., an in ascending order.
Request the sequence after the operation is completed. -
[input format]
The first line of input contains two integers n and m, which respectively represent the length of the sequence and the number of operations.
Next, line m describes the operation on the sequence, where line i contains two integers PI, and Qi represents the operation type and parameters. When pi = 0, it means that a1, a2,..., aqi are arranged in descending order; When pi = 1, it means aqi, aqi+1,..., an are arranged in ascending order;
-
[output format]
Output a line containing n integers, separated by a space between adjacent integers, indicating the sequence after the operation is completed.
-
[sample input]
3 3 0 3 1 2 0 2
-
[sample output]
3 1 2
-
[example description]
The original sequence is (1,2.3).
After step 1 is (3,2,1).
After step 2 is (3,1,2).
After step 3 is (3,1,2). The same as after step 2, because the first two numbers are in descending order. -
[evaluation case scale and agreement]
For 30% of the evaluation cases, n,m ≤ 1000;
For 60% of the evaluation cases, n,m ≤ 5000;
For all evaluation cases, 1 ≤ n,m ≤ 100000, 0 ≤ ai ≤ 1, 1 ≤ bi ≤ n.
answer
The first thing easy to think of is to use the sort function in c++STL
#include<bits/stdc++.h>
using namespace std;
bool cmp1(int a, int b) { //Ascending order
return a < b;
}
bool cmp2(int a, int b) { //Descending order
return a > b;
}
int main(){
vector<int>array;
int n, m;
int p, q;
cin>>n>>m;
for (int i = 1; i <= n; i++) {
array.push_back(i);
}
for (int i = 0; i < m; i++) {
cin>>p>>q;
if (p) {
sort(array.begin() + q - 1, array.end(), cmp1);
} else {
sort(array.begin(), array.begin() + q, cmp2);
}
}
for (int i = 0; i < n; i++) {
cout<<array[i]<<" ";
}
return 0;
}
This method can be used to do almost half of the samples, which is good for mixing.
Question:
- Too many operations, too much data, timeout!!!
Positive solution:
Idea:
- To perform m operations, each time either the prefix is arranged in descending order or the suffix is arranged in ascending order.
- When pi = 0, it means that a1, a2,..., aqi are arranged in descending order;
- When pi = 1, it means aqi, aqi+1,..., an are arranged in ascending order;
- At first, the given sequence is in ascending order by default, so the initial ascending operations are redundant.
- When the continuous pi = 0, the continuous prefix is arranged in descending order. You only need to sort once, a1, a2,..., aqi (record the maximum value of qi)
- Similarly, when the continuous pi = 1, the continuous suffix n is arranged in ascending order, which only needs to be sorted once, aqi, aqi+1,..., an (record the minimum value of qi)
- After the above simplification, the operation sequence becomes an alternating operation of pi = 0 and pi = 1. The first operation starts with pi = 0.
Further analysis:
- For the first effective operation, it is to arrange [1,x] in descending order. At first, the sequence is in ascending order, then ∀ ai ∈ [x + 1, n] > ∀ bi ∈ [0, x]
- At this time, the [1,x] part is sorted in descending order, and the [x+1, n] part is sorted in ascending order.
- After that, [y, n] is sorted in ascending order. When y > x, it is equivalent to no operation. When y < = x, [x + 1, n] does not change, that is, [x + 1, n] is fixed.
- After that, [1, z] is sorted in descending order. When Z < y, it is equivalent to no operation. When z > = y, [1, y - 1] does not actually change, that is, [1, y - 1] is fixed.
- Then fix the elements from both sides to the middle, and finally deal with the boundary.
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
vector<pair<int, int> > act(N); //Record each operation
vector<int> ans(N);
int main(){
int n, m;
int count = 0;
cin >> n >> m;
while (m--) {
int p, q;
cin >> p >> q;
if (!p) {
while (count && act[count].first == 0) { //Compress consecutive p = 0 operations
q = max(q, act[count--].second);
}
while (count >= 2 && act[count - 1].second <= q) {
//If the current operation is larger than the previous one, the first two operations will be invalidated
count -= 2;
}
act[++count] = {0, q};
} else if (count) {
while (count && act[count].first) { //Compress continuous p = 1 operation
q = min(q, act[count--].second);
}
while (count >= 2 && act[count - 1].second >= q) {
//If the current operation is larger than the previous one, the first two operations will be invalidated
count -= 2;
}
act[++count] = {1, q};
}
}
int left = 1;
int right = n;
int k = n;
for (int i = 1; i <= count; i++) { //assignment
if (act[i].first == 0) {
while (right > act[i].second && left < right + 1) {
ans[right--] = k--;
}
} else {
while (left < act[i].second && left < right + 1) {
ans[left++] = k--;
}
}
if (left > right) {
break;
}
}
if (count % 2) { //Boundary treatment
while (left < right + 1) {
ans[left++] = k--;
}
} else {
while (left < right + 1) {
ans[right--] = k--;
}
}
for (int i = 1; i <= n; i++) {
cout<<ans[i]<<" ";
}
return 0;
}
Question J: parenthesis sequence
Time limit: 1.0 s memory limit: 256.0 MB
-
[problem description]
Given a bracket sequence, it is required to add as few brackets as possible to make the bracket sequence legal. When the addition is completed, different addition results will be produced. How many essentially different addition results are there. The two results are essentially different, which means that there is a certain position. One result is the left parenthesis and the other is the right parenthesis.
For example, for the bracket sequence ((()), you only need to add two brackets to make it legal. There are several different adding results: () () (), () () () (), () (), and (()). -
[input format]
The input line contains a string s, which represents the given sequence of parentheses. There are only left and right parentheses in the sequence.
-
[output format]
Output an integer to represent the answer. The answer may be large. Please output the remainder of the answer divided by 100000007 (i.e. 109 + 7).
-
[sample input]
((()
-
[sample output]
5
-
[evaluation case scale and agreement]
For 40% of the evaluation cases, | s | ≤ 200.
For all evaluation cases, 1 ≤| s | ≤ 5000.
answer
Idea: dynamic programming
- The legal parenthesis sequence satisfies two conditions:
- The number of left parentheses must be equal to the number of right parentheses
- The number of left parentheses at any position must be greater than or equal to the number of right parentheses
-
Given the sequence of questions, we need to add left and right parentheses. The added parentheses can only be between the gaps of the sequence of parentheses.
-
Does the addition of left and right parentheses interfere with each other? (the answer is no interference)
-
If the left bracket and the right bracket add different gaps, they must not affect each other.
-
If the same gap is added:
- If it is added in the form of "()", the two will form a pair, which is contrary to adding as few brackets as possible in the title.
- The bracket can only be left and right. That is, the form of ") (".
- Therefore, adding left and right brackets can be calculated separately. The answer is the number of schemes with separate left parentheses multiplied by the number of schemes with separate right parentheses.
- Left parenthesis calculated separately:
- Divide with each right parenthesis as the boundary: XXX) XXX) XXX, XXX is several left parentheses.
- We only need to consider adding some left parentheses before the right parentheses to ensure that the sequence is a legal sequence.
- The right bracket is preceded by the left bracket, so the number of schemes adding the left bracket only corresponds to the number of schemes adding the left bracket.
- Design status dp[i][j]: indicates that only the first I parentheses are considered, and there are j more left parentheses than right parentheses.
- Finally, just enumerate from dp[n][0] to dp[n][n] and return the first reasonable number of schemes. (n is the initial number of parentheses. At this time, the minimum number of parentheses can be added)
-
When the current bracket is an open bracket, dp[i][j] = dp[i - 1][j - 1]
-
When the current bracket is a closing bracket:
- The range of left parentheses added before is [0, j + 1]
- The corresponding number of schemes is [i] [J - 1] [DP], respectively
- Therefore, DP [i] [J] = DP [I - 1] [J + 1] + DP [I -] + DP [I - 1] [J - 1] +... + dp[i - 1][0]
- Because: dp[i][j - 1] = dp[i - 1][j] + dp[i - 1][j - 1] +... + dp[i - 1][0]
- So: dp[i][j] = dp[i - 1][j + 1] + dp[i][j - 1]
-
Calculate the right bracket separately:
According to the symmetry, reverse the original bracket sequence, then change all the left brackets into right brackets, and the right brackets into left brackets. Finally, calculate the left bracket separately, that is, calculate the right bracket separately.
#include<bits/stdc++.h>
using namespace std;
const int N = 5010;
const int mod = 1e9 + 7;
int n;
char str[N];
long long dp[N][N];
long long compute() {
memset(dp, 0, sizeof(dp));
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
if (str[i] == '(') {
for (int j = 1; j <= n; j++) {
dp[i][j] = dp[i - 1][j - 1];
}
} else {
dp[i][0] = (dp[i - 1][0] + dp[i - 1][1]) % mod; //The boundary is treated separately
for (int j = 1; j <= n; j++) {
dp[i][j] = (dp[i - 1][j + 1] + dp[i][j - 1]) % mod;
}
}
}
for (int i = 0; i <= n; i++) { //Number of schemes for finding the shortest legal sequence
if (dp[n][i]) {
return dp[n][i];
}
}
return -1;
}
int main(){
scanf("%s", str + 1); //Subscripts are read in from 1
n = strlen(str + 1); //Bracket sequence length
long long l = compute();
reverse(str + 1, str + n + 1); //Reverse bracket sequence
for (int i = 1; i <= n; i++) { //Transform left and right parentheses
if (str[i] == '(') {
str[i] = ')';
} else {
str[i] = '(';
}
}
long long r = compute();
cout << l * r % mod << endl;
return 0;
}
Summary:
The result is OK. Save two. Blue Bridge Cup, you have really changed. To put it bluntly, it's still too delicious 😅 Continue to work hard in the next Blue Bridge Cup and strive to enter the national competition! (╯ dish ▔) ╯