OK, I'm here again. I have to write the supplementary questions for a long time every time. The teacher's questions are very good. I'm too delicious to make up the questions carefully~
The code should always be AC code written by myself. I'm not used to the beautiful code of teachers and brothers. I can't understand it,,,
A Alice and Bob
os: I don't know where to find this strange figure: P
Idea: there's no idea about the check-in question. Just pay attention to the data range and open long long (don't have unnecessary WA, you can't afford to hurt in 20 minutes!)
AC Code:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stack>
#include <vector>
#include <map>
#include <queue>
#include <cstring>
#include <cmath>
#include <set>
#include <iterator>
#include <numeric>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
//Judge whether to open ll!!!
//Determine whether initialization is required!!!
const int mod=1e9+7;
ll a,b;
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
ios;
cin>>a>>b;
cout<<a+b<<'\n';
return 0;
}
B Accepted (check-in, string simulation)
Idea: the enumeration needs to be modified several times from the first character to the first eight characters i-7 before it is accepted. If the string length is less than 8, it will directly output - 1 without solution.
AC Code:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stack>
#include <vector>
#include <map>
#include <queue>
#include <cstring>
#include <cmath>
#include <set>
#include <iterator>
#include <numeric>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
//Judge whether to open ll!!!
//Determine whether initialization is required!!!
const int mod=1e9+7;
int t;
int n;
string s;
int countt(string s)
{
int cnt=0;
if(s[0]=='a') cnt++;
if(s[1]=='c') cnt++;
if(s[2]=='c') cnt++;
if(s[3]=='e') cnt++;
if(s[4]=='p') cnt++;
if(s[5]=='t') cnt++;
if(s[6]=='e') cnt++;
if(s[7]=='d') cnt++;
return cnt;
}
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
cin>>t;
while(t--)
{
cin>>n;
cin>>s;
if(n<8)
cout<<"-1"<<'\n';
else
{
int maxn=-1;
for(int i=0;i<n-7;i++)
{
maxn=max(maxn,countt(s.substr(i,8)));
}
cout<<8-maxn<<'\n';
}
}
return 0;
}
ps: the first two questions are still A. they are very fast, a total of 28 minutes (HA for me), but not so much later
C fast break man's breakfast (ruler method, prefix and + two-point search)
Nonsense can be skipped: obviously, direct violence simulation must TLE
Idea: this problem is a classical problem of ruler taking. For each position l ruler, take out the maximum legal position of its corresponding R, then the contribution of L is R − l + 1, and the time complexity is O(n). Or you can first count the prefix sum of the number of 0, and then dichotomize r for each L, contributing the same reason, time complexity O(nlogn).
Add: ruler taking method (the first time I heard this expression...), It is generally to find the "optimal continuous subsequence" which is not greater than an upper limit in a given set of data.
AC Code:
(1) Ruler taking method: (only after reading other people's code can we understand how to simulate, and the code ability needs to be improved)
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stack>
#include <vector>
#include <map>
#include <queue>
#include <cstring>
#include <cmath>
#include <set>
#include <iterator>
#include <numeric>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
//Judge whether to open ll!!!
//Determine whether initialization is required!!!
const int mod=1e9+7;
int t;
int n,k;
string s;
int cnt;
ll ans;
int l,r;
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
cin>>t;
while(t--)
{
cin>>n>>k;
cin>>s;
l=0,r=0,cnt=0,ans=0;
while(r<n)
{
if(s[r]=='0')
++cnt;
while(cnt>k&&l<=r)//The position of l is updated at the same time, and there is no need for two-level loop nesting
{
if(s[l]=='0')
--cnt;
l++;
}
ans+=r-l+1;
r++;
}
cout<<ans<<'\n';
}
return 0;
}
The approximate operation is: starting from l=0, calculate the number of 0 when r gradually increases. When it is greater than the given value, l moves one bit to the right, and calculate the contribution of legal L and r at the same time.
(2) Prefix and + binary STL solution:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stack>
#include <vector>
#include <map>
#include <queue>
#include <cstring>
#include <cmath>
#include <set>
#include <iterator>
#include <numeric>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
//Judge whether to open ll!!!
//Determine whether initialization is required!!!
const int mod=1e9+7;
const int N=1e5+10;
int dif[N];
int t,n,k;
string s;
ll ans;
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
cin>>t;
while(t--)
{
memset(dif,0,sizeof(dif));
cin>>n>>k;
cin>>s;
if(s[0]=='0')
dif[0]=1;
else
dif[0]=0;
for(int i=1;i<n;i++)
{
if(s[i]=='0')
dif[i]=dif[i-1]+1;
else
dif[i]=dif[i-1];
}
ans=0;
for(int i=0;i<n;i++)
{
ans+=upper_bound(dif,dif+n,dif[i-1]+k)-dif-i;
}
cout<<ans<<'\n';
}
return 0;
}
ps: the elder martial brother mentioned the lower in STL when he talked about two points before_ Bound () and upper_bound() but I haven't used it. I've learned,,,
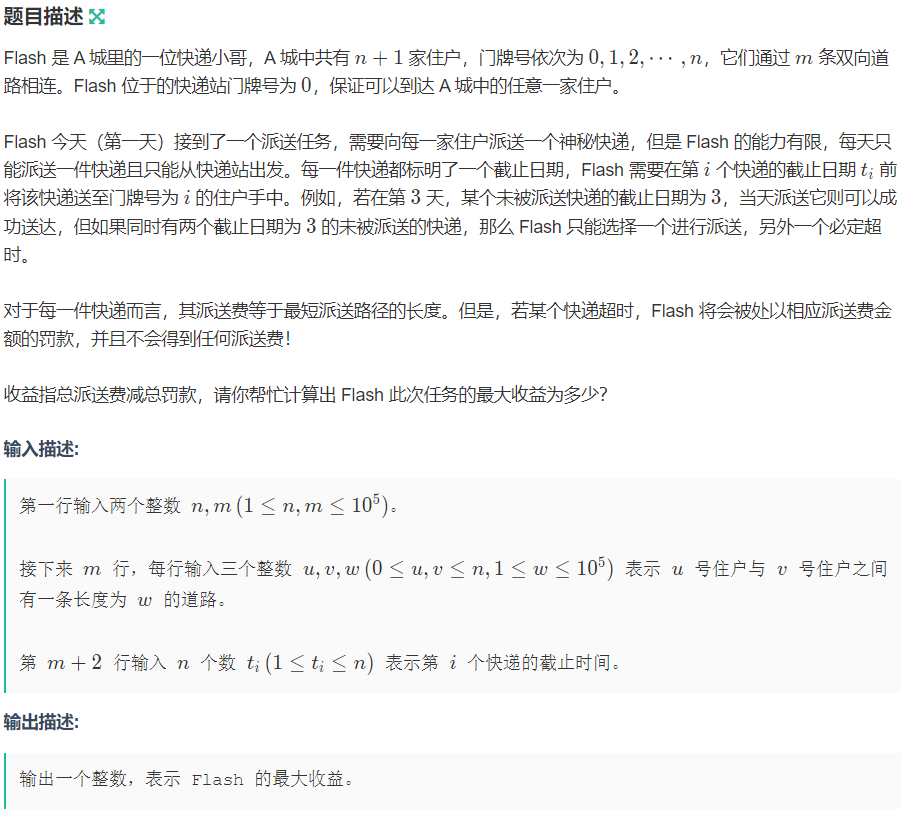
D express delivery (shortest path + greedy?)
Nonsense can be skipped: I just talked about the shortest path a few days before the end of the training competition. I haven't fully understood QWQ. After the end of the exam, I must do a good job in graph theory. I'm too bad
Idea: deal with the shortest path dis[i] from point 0 to point I, that is, the delivery fee or fine of express I, and then sort it from small to large according to the deadline of express. Just be a repentant greedy, specifically to maintain a small root pile and store the delivery fee of the express delivery planned to be delivered in the pile. Scan all couriers from front to back. For No. I express, if the size of the stack is less than the deadline of No. I express, it indicates that the express can be delivered normally; Otherwise, compare the size of dis[i] with the top of the stack. If dis[i] is larger than the top of the stack, it means that it is better to send No. I express instead of top of the stack. Otherwise, it is better to send No. I express instead of top of the stack. Time complexity O(nlogn + nlogm).
(I haven't used the priority queue much before...)
AC Code: (after reading elder martial brother's code, I understand what happened. Part of the explanation is in the notes)
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
//Judge whether to open ll!!!
//Determine whether initialization is required!!!
const int mod=1e9+7;
const int N=2e5+10;
ll n,m;
int head[N],cnt;
ll dis[N];
bool vis[N];
struct node
{
ll to,next,w;
} e[N];
void addedge(int x,int y,ll z)//Chained forward star plus edge function
{
e[++cnt].w=z;
e[cnt].to=y;
e[cnt].next=head[x];
head[x]=cnt;
}
struct people
{
int time;
ll dis;
} a[N];
bool cmp(people a,people b)
{
if(a.dis>b.dis) return true;
else if(a.dis==b.dis&&a.time<b.time) return true;
else return false;
}
void dijkstra(int s)//Dijkstra handles the shortest circuit from point 0 to point i
{
memset(dis,0x3f,sizeof(dis));
priority_queue<pair<ll,int>,vector<pair<ll,int>>,greater<pair<ll,int>>>q;
q.push({0,s});
dis[s]=0;
while(!q.empty())
{
int now=q.top().second;//now is the number of points
q.pop();
if(vis[now])
continue;
vis[now]=1;
for(int i=head[now];i;i=e[i].next)
{
int to=e[i].to;
if(dis[to]>dis[now]+e[i].w)
{
dis[to]=dis[now]+e[i].w;
q.push({dis[to],to});
}
}
}
}
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
cin>>n>>m;
for(int i=1;i<=m;i++)
{
int x,y,z;
cin>>x>>y>>z;
addedge(x,y,z);
addedge(y,x,z);//Undirected graph, two-way edge
}
dijkstra(0);
for(int i=1;i<=n;i++)
{
cin>>a[i].time;
a[i].dis=dis[i];
}
sort(a+1,a+1+n,cmp);
memset(vis,0,sizeof(vis));
ll ans=0;
int l=1;
for(int i=1;i<=n;i++)
{
if(!vis[a[i].time])
{
ans+=a[i].dis;
vis[a[i].time]=1;
}
else
{
int k=a[i].time-1;
while(vis[k]&&k>=1)
--k;//With repentant greed
if(!vis[k]&&k>=1)
vis[k]=1,ans+=a[i].dis;
else
ans-=a[i].dis;
}
}
cout<<ans<<'\n';
return 0;
}
os: with repentance of greed, this method is also the first time to see,,, learn
H abusing prime
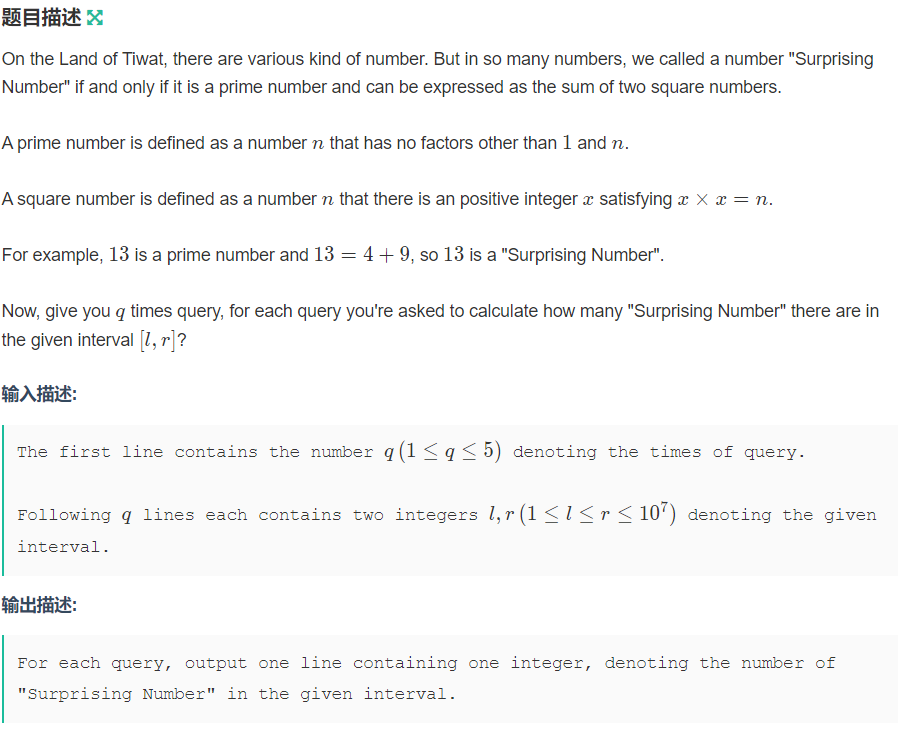
Definition: surprising prime is a prime number that can be written as the sum of two square numbers. Find the number of such numbers in a given interval.
Nonsense can be skipped: although it's an English question, it's still very understandable. At first, I tried to find the law, but I didn't find it. If I feel violent, I 1e7 shouldn't be very good. As a result, it turns out to be OK,,,
Idea: it's easy to find the rule by typing the table. Surprising Prime is a prime number with 2 or module 4 as 1. It's troublesome to prove it. You can baidu by yourself. (can you guess what else to prove
In addition, violent practices are as follows:
First, observe the data range [1, 107], pre process the prime numbers with a linear sieve, and then we find that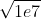
=3162, directly process the square number within the range of [1, 107], and then violently enumerate to find the prime number that can be expressed by the sum of two square numbers within the range of [1, 107], mark the number contribution to the answer as true, and then prefix and preprocess from [1, 107]. Answer the question directly with O(1). (pasted solution written by elder martial brother: P)
AC Code:
(1) According to the law:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stack>
#include <vector>
#include <map>
#include <queue>
#include <cstring>
#include <cmath>
#include <set>
#include <iterator>
#include <numeric>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
//Judge whether to open ll!!!
//Determine whether initialization is required!!!
const int mod=1e9+7;
const int N=1e7+10;
int prime[N];
bool mark[N];
int tot;
int q,l,r;
void oula()
{
mark[1]=true;
for(int i=2;i<=N;i++)
{
if(!mark[i])
prime[++tot]=i;
for(int j=1;j<=tot;j++)
{
if(i*prime[j]>N)
break;
mark[i*prime[j]]=true;
if(i%prime[j]==0)
break;
}
}
}
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
cin>>q;
oula();
while(q--)
{
cin>>l>>r;
int cnt=0;
for(int i=l;i<=r;i++)
{
if(!mark[i]&&i==2)
++cnt;
if(!mark[i]&&i%4==1)
++cnt;
}
cout<<cnt<<'\n';
}
return 0;
}
(2) Violence:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stack>
#include <vector>
#include <map>
#include <queue>
#include <cstring>
#include <cmath>
#include <set>
#include <iterator>
#include <numeric>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
//Judge whether to open ll!!!
//Determine whether initialization is required!!!
const int mod=1e9+7;
const int N=1e7+10;
int prime[N];
bool mark[N];
bool b[N*2];
int tot;
int q,l,r;
void oula()
{
mark[1]=true;
for(int i=2;i<=N;i++)
{
if(!mark[i])
prime[++tot]=i;
for(int j=1;j<=tot;j++)
{
if(i*prime[j]>N)
break;
mark[i*prime[j]]=true;
if(i%prime[j]==0)
break;
}
}
}
void pan()
{
for(int i=1;i<=sqrt(10000000);i++)
{
for(int j=1;j<=sqrt(10000000);j++)
{
b[i*i+j*j]=true;
}
}
}
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
cin>>q;
oula();
pan();
while(q--)
{
cin>>l>>r;
int cnt=0;
for(int i=l;i<=r;i++)
{
if(!mark[i]&&b[i])
++cnt;
}
cout<<cnt<<'\n';
}
return 0;
}
J excursion (simulation)
Nonsense can be skipped: I have been working on this problem since I solved the first two questions in half an hour. At first, I thought it was similar to LIS problem, wrote DP for half a day, and found that it was a continuous interval. I didn't read the problem carefully, which hurt me. Then I began to simulate it with ordinary methods, straight WA, but finally I did it (too difficult QWQ)
Idea: I opened two arrays, traversing from front to back to find out the length that does not decrease, and then traversing from back to front to find out the degree of non progressive growth, adding them one by one, and the biggest one is the answer.
AC Code:
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <stack>
#include <vector>
#include <map>
#include <queue>
#include <cstring>
#include <cmath>
#include <set>
#include <iterator>
#include <numeric>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
//Judge whether to open ll!!!
//Determine whether initialization is required!!!
const int mod=1e9+7;
const int N=5e5+5;
int n;
int a[N],b[N],c[N];
int maxn1,maxn2;
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
for(int i=1;i<=n;i++)
b[i]=1,c[i]=1;
for(int i=2;i<=n;i++)
{
if(a[i]>=a[i-1])
b[i]=b[i-1]+1;
maxn1=max(maxn1,b[i]);
}
for(int i=n-1;i>=1;i--)
{
if(a[i]>=a[i+1])
c[i]=c[i+1]+1;
maxn2=max(maxn2,c[i]);
}
int ans=-1;
for(int i=1;i<=n;i++)
{
ans=max(ans,c[i]+b[i]);
}
cout<<ans-1<<'\n';
return 0;
}
M - XCPX (violence / diagonal prefix and)
Idea: violence is enough. The standard solution uses the diagonal prefix and.
AC Code:
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define ios ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define INF 0x3f3f3f3f
//Judge whether to open ll!!!
//Determine whether initialization is required!!!
const int mod=1e9+7;
int t,n,m,q,x,y,s;
bool check(int x,int y)
{
if(x>=1&&x<=n&&y>=1&&y<=m) return true;
else return false;
}
int main()
{
// freopen("test.in","r",stdin);
// freopen("output.in", "w", stdout);
ios;
cin>>t;
while(t--)
{
cin>>n>>m>>q;
int c[n+3][m+3];
memset(c,0,sizeof(c));
while(q--)
{
cin>>x>>y>>s;
c[x][y]++;
for(int i=1;i<=s;i++)
{
int nx=x+i,ny=y+i;
if(!check(nx,ny)) break;
c[nx][ny]++;
}
for(int i=1;i<=s;i++)
{
int nx=x-i,ny=y+i;
if(!check(nx,ny)) break;
c[nx][ny]++;
}
for(int i=1;i<=s;i++)
{
int nx=x+i,ny=y-i;
if(!check(nx,ny)) break;
c[nx][ny]++;
}
for(int i=1;i<=s;i++)
{
int nx=x-i,ny=y-i;
if(!check(nx,ny)) break;
c[nx][ny]++;
}
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
cout<<c[i][j]<<" \n"[j==m];
}
}
return 0;
}
os: the data bar should be, otherwise the two-dimensional array with the maximum storage range cannot be opened
Two months after the end of the training competition, I have to fill in the questions. I haven't finished yet. Come on
If there is any mistake, please advise orzorz