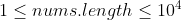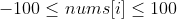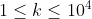catalogue

Maximized array sum after K negations

describe

Example 1

Example 2

Example 3

Tips

Method 1: violence ranking

Method 2: modify negative numbers

Method 3: sorting improvement

Maximized array sum after K negations

describe

Give you an integer array nums and an integer k. modify the array as follows:

Select a subscript I   And replace num [i] with - num [i].
Repeat this process exactly k times. You can select the same subscript i multiple times.

When the array is modified in this way, the maximum possible sum of the array is returned.

Example 1

Input: nums = [4,2,3], k = 1
 Output: 5
 Explanation: select subscript 1, nums Become [4,-2,3] 

Example 2

Input: nums = [3,-1,0,2], k = 3
 Output: 6
 Explanation: select subscript (1, 2, 2) ，nums Become [3,1,0,2] 

Example 3

Input: nums = [2,-3,-1,5,-4], k = 2
 Output: 13
 Explanation: select subscript (1, 4) ，nums Become [2,3,-1,5,4] 

Tips

• 
• 
• 

Method 1: violence ranking

For each sorting, the minimum value is taken for inversion

class Solution {
    public int largestSumAfterKNegations(int[] nums, int k) {
        for (int i = 0; i < k; i++) {
            Arrays.sort(nums);
            nums[0]=-nums[0];
        }
        int res=0;
        for (int i = 0; i < nums.length; i++) res+=nums[i];
        return res;
    }
}

 

Method 2: modify negative numbers

Since we want the sum of the array to be as large as possible, unless we have to, we should always modify the negative number and give priority to the negative number with the smallest value. This greedy operation is optimal because changing the negative number - x to x will increase the sum of the array by 2x.

When the given K is less than or equal to the number of negative numbers in the array, we can modify each negative number from small to large according to the above method. But if the value of K is large, we have to modify the non negative number (i.e. positive number or 0). Since modifying 0 will not affect the sum of the array, and modifying a positive number will reduce the sum of the array, therefore:

• If 0 exists in the array
  • Then we can modify it many times until the remaining modification times are used up;
• If 0 does not exist in the array
  • If the number of modifications remaining is even
    • Since modifying the same number twice is equivalent to not modifying it, we can also use up the modification times without reducing the sum of the array;
  • If the remaining number of modifications is odd
    • Then we must use a single modification to change a positive number into a negative number (if the remaining modifications are even, the sum of the array will not be reduced). In order to make the sum of the array as large as possible, we choose the smallest positive number. It should be noted that during the previous process of changing negative numbers to positive numbers, smaller positive numbers may appear (compared with the smallest positive number in the original array), which cannot be ignored.

In order to implement the above algorithm, we can sort the array in ascending order, first traverse each negative number in turn (modify the negative number to a positive number), and then traverse all numbers (modify 0 or the smallest positive number).

However, note that the range of array elements in this question is [- 100, 100], so we can use the count array (bucket) or hash table to directly count the number of occurrences of each element, and then traverse the range of elements in ascending order, so as to save the time required for sorting.

class Solution {
    public int largestSumAfterKNegations(int[] nums, int k) {
        Map<Integer, Integer> freq = new HashMap<Integer, Integer>();
        for (int num : nums) {
            freq.put(num, freq.getOrDefault(num, 0) + 1);
        }
        int ans = Arrays.stream(nums).sum();
        for (int i = -100; i < 0; ++i) {
            if (freq.containsKey(i)) {
                int ops = Math.min(k, freq.get(i));
                ans += (-i) * ops * 2;
                freq.put(i, freq.get(i) - ops);
                freq.put(-i, freq.getOrDefault(-i, 0) + ops);
                k -= ops;
                if (k == 0) {
                    break;
                }
            }
        }
        if (k > 0 && k % 2 == 1 && !freq.containsKey(0)) {
            for (int i = 1; i <= 100; ++i) {
                if (freq.containsKey(i)) {
                    ans -= i * 2;
                    break;
                }
            }
        }
        return ans;
    }
}

 

Method 3: sorting improvement

class Solution {
    public int largestSumAfterKNegations(int[] nums, int k) {
        // Sort, ranking possible negative numbers first
        Arrays.sort(nums);
        int sum = 0;
        for (int i = 0; i < nums.length; i++) {
            // Greed: if it is negative and k still has a surplus, turn the negative number back
            if (nums[i] < 0 && k > 0) {
                nums[i] = -1 * nums[i];
                k--;
            }
            sum += nums[i];
        }
        Arrays.sort(nums);
        // If k is not left, it means that all the negative numbers that can be turned to positive, which is the maximum sum, and returns sum
        // If k is left, it means that all negative numbers have become positive. Therefore, if k has even numbers left, it will be offset by itself without deletion. If k has odd numbers left, it will be reduced by twice the minimum positive number.
        return sum - (k % 2 == 0 ? 0 : 2 * nums[0]); 
    }
}