2022-01-23: force buckle 425, word box.
Given a word set (no repetition), find all the word boxes in it.
A word sequence forms a valid word box, which means that it is the same string from row k and column k (0 ≤ k < max (number of rows and columns)).
For example, the word sequence "ball","area","lead","lady" forms a word box because each word is the same from the horizontal and vertical directions.
be careful:
The number of words is greater than or equal to 1 and not more than 500.
All words are of the same length.
The word length is greater than or equal to 1 and no more than 5.
Each word contains only lowercase letters a-z.
Answer 2022-01-23:
Recursion. All prefixes of all words will become key s.
be careful! There was a little mistake when introducing the topic setting in class
The title is described as follows:
Given n strings and the length of each string must be n, please form a word matrix, such as:
Given four strings, the length is 4, "ball","area","lead","lady"
The following square matrix can be formed:
b a l l
a r e a
l e a d
l a d y
What is word matrix? As can be seen from the square array above,
Row 1 and column 1 are "ball", row 2 and column 2 are "area", row 3 and column 3 are "lead", and row 4 and column 4 are "lady"
Therefore, if there are N words, the word matrix refers to:
An N*N two-dimensional matrix, and row i and column i are certain words. It is not required that all N words are in this square matrix.
Please return to all possible word matrices.
Example:
Input: words = "abat","baba","atan","atal"
Output: ["baba","abat","baba","atal","baba","abat","baba","atan"]
Explanation:
You can see that there are two linked lists in the output, representing two word matrices
The first one is as follows:
b a b a
a b a t
b a b a
a t a l
There is no atan in this matrix, because all words are not required to be in the matrix
The second is as follows:
b a b a
a b a t
b a b a
a t a n
There is no atal in this matrix, because all words are not required to be in the matrix
What the class said is: an N*N two-dimensional matrix, and row i and column i are certain words. All N words are required to be in this square matrix
The original question is: an N*N two-dimensional matrix, and row i and column i are certain words. It is not required that all N words are in this square matrix
The process is correct, but there is a mistake when introducing the meaning of the topic
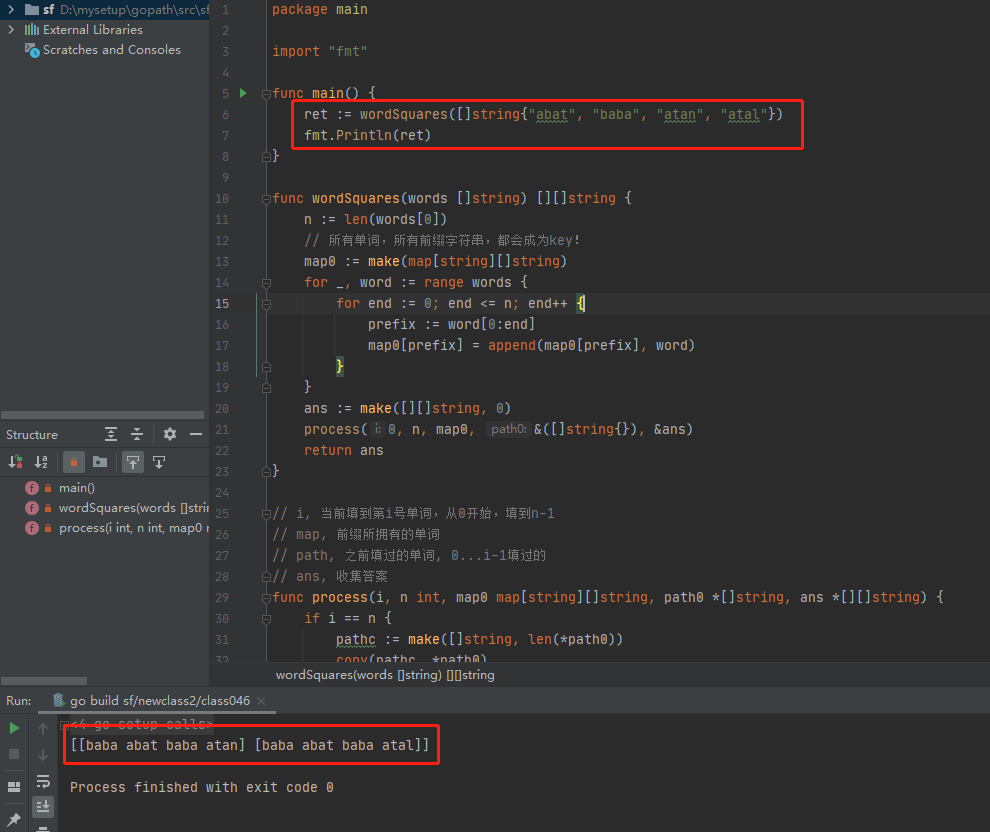
The code is written in golang. The code is as follows:
package main
import "fmt"
func main() {
ret := wordSquares([]string{"abat", "baba", "atan", "atal"})
fmt.Println(ret)
}
func wordSquares(words []string) [][]string {
n := len(words[0])
// All words, all prefix strings, will become key s!
map0 := make(map[string][]string)
for _, word := range words {
for end := 0; end <= n; end++ {
prefix := word[0:end]
map0[prefix] = append(map0[prefix], word)
}
}
ans := make([][]string, 0)
process(0, n, map0, &([]string{}), &ans)
return ans
}
// i. Currently, fill in word I, starting from 0 to n-1
// map, the word owned by the prefix
// path, previously filled word, 0 I-1 filled
// ans, collect answers
func process(i, n int, map0 map[string][]string, path0 *[]string, ans *[][]string) {
if i == n {
pathc := make([]string, len(*path0))
copy(pathc, *path0)
*ans = append(*ans, pathc)
} else {
// Find out the limit, the limit of prefix!
builder := make([]byte, 0)
for _, pre := range *path0 {
builder = append(builder, pre[i])
}
prefix := string(builder)
if _, ok := map0[prefix]; ok {
for _, next := range map0[prefix] {
*path0 = append(*path0, next)
process(i+1, n, map0, path0, ans)
*path0 = (*path0)[0 : len(*path0)-1]
}
}
}
}The results are as follows: