Question 1:
Given the root node of a binary search tree , root and an integer , k, please design an algorithm to find the , k , smallest element (counting from 1).
Example 1:
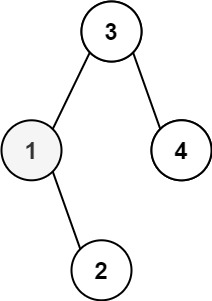
Input: root = [3,1,4,null,2], k = 1 Output: 1
Example 2:
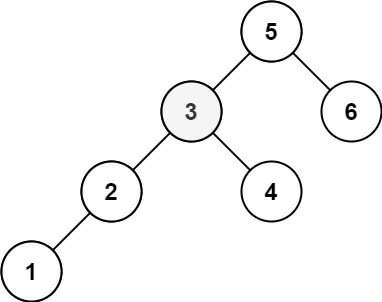
Input: root = [5,3,6,2,4,null,null,1], k = 3 Output: 3
Tips:
- The number of nodes in the tree is n.
- 1 <= k <= n <= 104
- 0 <= Node.val <= 104
Advanced: if the binary search tree is often modified (insert / delete operation) and you need to frequently find the value of the ^ k ^ small, how will you optimize the algorithm?
1 /** 2 * Definition for a binary tree node. 3 * public class TreeNode { 4 * int val; 5 * TreeNode left; 6 * TreeNode right; 7 * TreeNode() {} 8 * TreeNode(int val) { this.val = val; } 9 * TreeNode(int val, TreeNode left, TreeNode right) { 10 * this.val = val; 11 * this.left = left; 12 * this.right = right; 13 * } 14 * } 15 */ 16 class Solution { 17 public int kthSmallest(TreeNode root, int k) { 18 int left=size(root.left); 19 if (left==k-1) return root.val; 20 if (left>k-1) return kthSmallest(root.left,k); 21 else return kthSmallest(root.right,k-left-1); 22 } 23 24 public int size(TreeNode root) { 25 if (root==null) return 0; 26 return size(root.left)+size(root.right)+1; 27 } 28 29 }
Idea: according to the nature of binary} search tree, the root nodes are smaller on the left and larger on the right, so the number of left subtrees is left, and the root node is the number left+1.
Therefore, if the left node left==k-1, the root node is the k-th number. When left > k-1, it means that the k-th is in the left subtree, and the recursive call is used to find the k-th in the left subtree;
If left < k-1, it means that in the right subtree, recursive call is used to find k-left-1 in the right subtree.
Question 2:
Give the root node of the binary search tree , the node values of which are different. Please convert it into a Greater Sum Tree so that the new value of , node , of each node is equal to or greater than , node in the original tree The sum of the values of Val +.
Remind me that the binary search tree meets the following constraints:
- The left subtree of a node contains only nodes whose key is less than the node key.
- The right subtree of a node contains only nodes whose key is greater than the node key.
- The left and right subtrees must also be binary search trees.
Note: this question and 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ Same
Example 1:
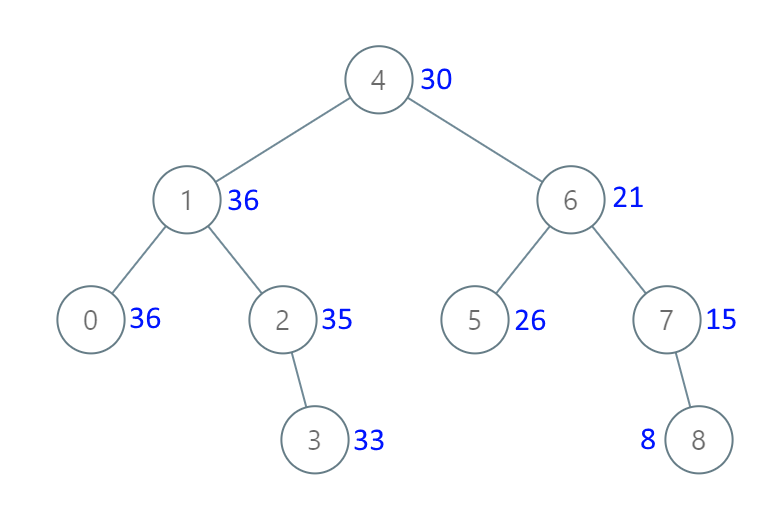
Input: [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
Example 2:
Input: root = [0,null,1] Output: [1,null,1]
Example 3:
Input: root = [1,0,2] Output: [3,3,2]
Example 4:
Input: root = [3,2,4,1] Output: [7,9,4,10]
Tips:
- The number of nodes in the tree is between 0 and 104.
- The value of each node is between - 104 ¢ and 104 ¢.
- All values {in the tree are different from each other.
- The given tree is a binary search tree.
1 /** 2 * Definition for a binary tree node. 3 * public class TreeNode { 4 * int val; 5 * TreeNode left; 6 * TreeNode right; 7 * TreeNode() {} 8 * TreeNode(int val) { this.val = val; } 9 * TreeNode(int val, TreeNode left, TreeNode right) { 10 * this.val = val; 11 * this.left = left; 12 * this.right = right; 13 * } 14 * } 15 */ 16 class Solution { 17 int sum; 18 public TreeNode convertBST(TreeNode root) { 19 build(root); 20 return root; 21 } 22 23 24 public void build(TreeNode root) { 25 if (root==null) return; 26 build(root.right); 27 sum+=root.val; 28 root.val=sum; 29 build(root.left); 30 } 31 }
Idea: the middle order traversal is sorted from small to large, and vice versa. sum is accumulated from large to small, and then change the value of the current node, which can be generated recursively from large to small.