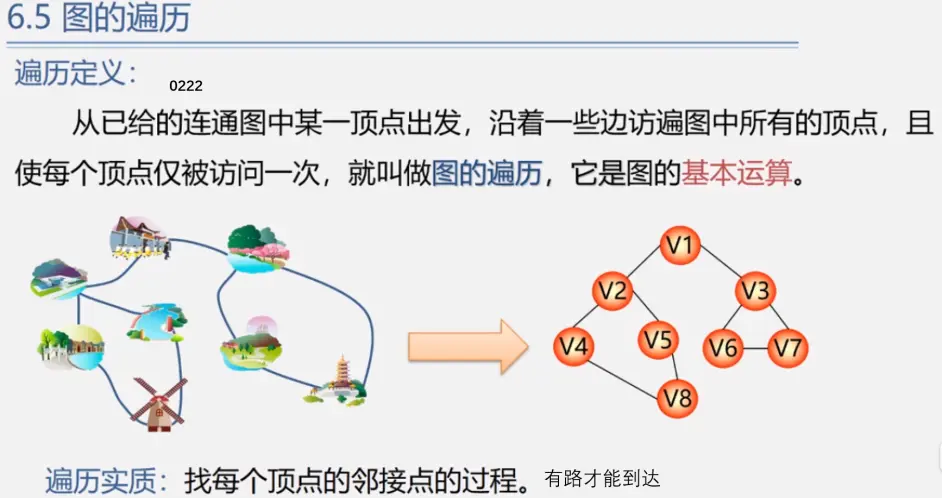
Traversal of Graphs

concept

Depth first traversal

The specific method of DFS (depth first search) algorithm is: go deep from a certain point. When you can't go down, go back to the previous step until you find the solution or finish all the points.

When implementing this sequential access order, the idea of operation action storage is similar to that of data structure (stack). At the same time, due to the nature of stack, we can simplify the creation of stack by recursion. Therefore, the two methods of DFS algorithm are implemented by stack or recursion respectively.

Algorithm steps (recursive or stack implementation)

a) Visit the specified starting point.

b) If the adjacent vertex of the currently accessed vertex has a vertex that has not been accessed, select any one to access. If not, it will fall back to the most recently accessed vertex until all points connected with the starting vertex are traversed.

c) If there are still vertices on the way that have not been accessed, select another point as the starting vertex and repeat the previous steps.


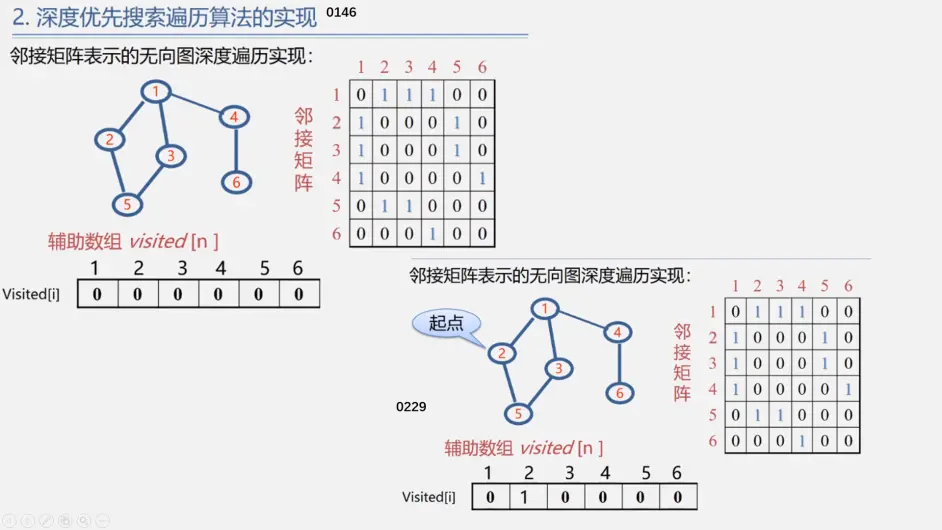
2 after accessing, select one of the adjacent points of 2 that are not accessed (while the adjacent point of No. 2 is stored in the row with subscript 2 in the adjacent matrix, and then find the premise value in sequence. If it must be 1, the network is the weight (non-0); Not accessed < see if the value corresponding to the visit array is 0 >) 2 – > 1. After accessing 1, modify visited[1]=1 – > find the adjacency point of 1 that has not been accessed (the subscript of the line is 1. This line judges in turn < the first no value is 0, while looking at the next value is 1visited. The value of the array is 1. After accessing > continue to look at the next No. 3, it is OK) 1 – "3. After accessing 3, modify visited[3]=1... 3 –" 5, (5 the first adjacency point 2 has been visited, and the second adjacency point 3 has also been visited) –? Fallback 3 – "fallback 1 –" 4 – "6 –" fallback to 4 – "fallback 1 –" fallback 2 (fallback starting point) access complete

DFS access result: 2 – > 1 – > 3 – > 5 – > 4 – > 6 (storage structure determination - result determination)

realization

DFS The relevant templates of the algorithm are as follows:

void dfs()//Parameters are used to indicate status  
{  
    if(End state)  
    {  
        ...//Add as needed  
        return;  
    }  
    if(Out of bounds or illegal)  
        return;  
    if(Special state)//Prune and remove some scenes that don't need to be visited, not necessarily i my home
        return ;
    for(Expansion mode)  
    {  
        if(The status reached by the extension method is legal)  
        {  
            Modify operation;//Add according to the meaning of the question  
            Marking;  
            dfs()；  
            (Restore tag)；  
            //Whether to restore the mark according to the meaning of the question  
            //If you add (restore mark), it is the backtracking method  
        }  
  
    }  
}
For graph theory (code excerpt, for reference only, please remember the code of the template above):

//Starting from the pos point, the depth traverses the undirected graph
//pos represents the current node, G represents the diagram, and the visited [] array is used to indicate whether the node has been accessed
void DFS(int pos,pGraph G,int visited[30]){
    node p;
    printf("%d ",pos);//Print depth traversal points
    visited[pos]=1;//Mark as visited
    p=G->vertice[pos].firstarc;//Assign the first pointer of the current point to p
    //Is there an adjacency point
    while(p!=NULL) {
        //Judge whether the adjacent contact has been traversed
        if(visited[p->adjvex]==0){
            DFS(p->adjvex,G,visited);
        }
        p=p->next;//Move back one bit to prepare whether there are adjacent contacts in the future
    }
}

breadth-first search

BFS algorithm and its core idea is to walk through its adjacent points from a certain point, and then choose any adjacent point to walk through the non traversed points adjacent to it, so as to walk through all nodes repeatedly. Sequence traversal similar to a tree.

The core of BFS is to store the current location as a status and give the status to the queue for queue entry operation,

Algorithm steps (implemented with queue)

a) Access the specified starting point.

b) The adjacent vertices accessing the current vertex have vertices that are not accessed, and put them in the queue.

c) Delete the queue head node of the queue. To access the head of the current queue, follow the previous steps. Until the queue is empty.

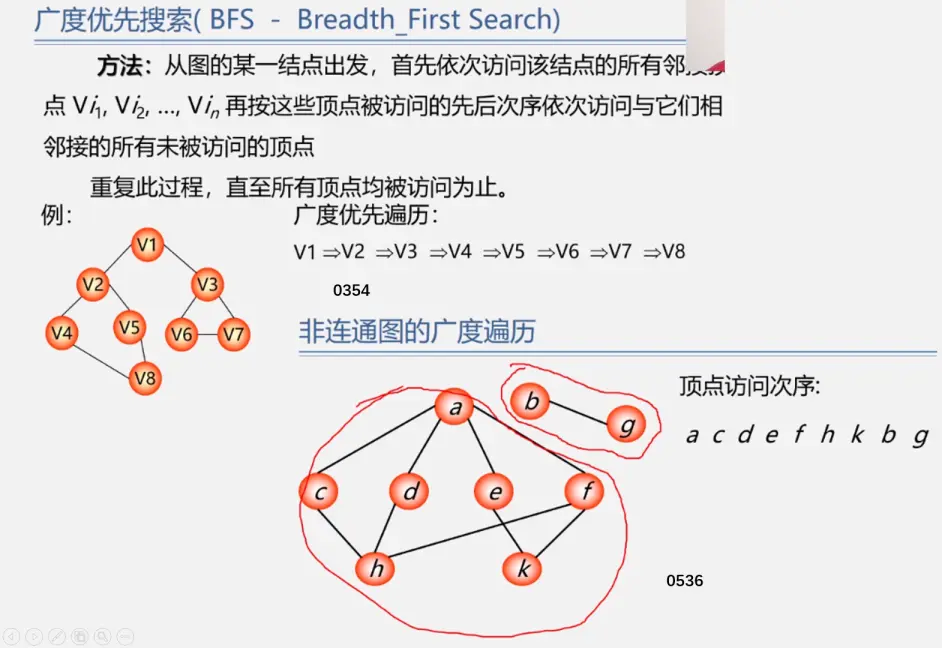
d) If there are still vertices on the way that have not been accessed, select another point as the starting vertex. Repeat the previous steps. (for unconnected graphs).

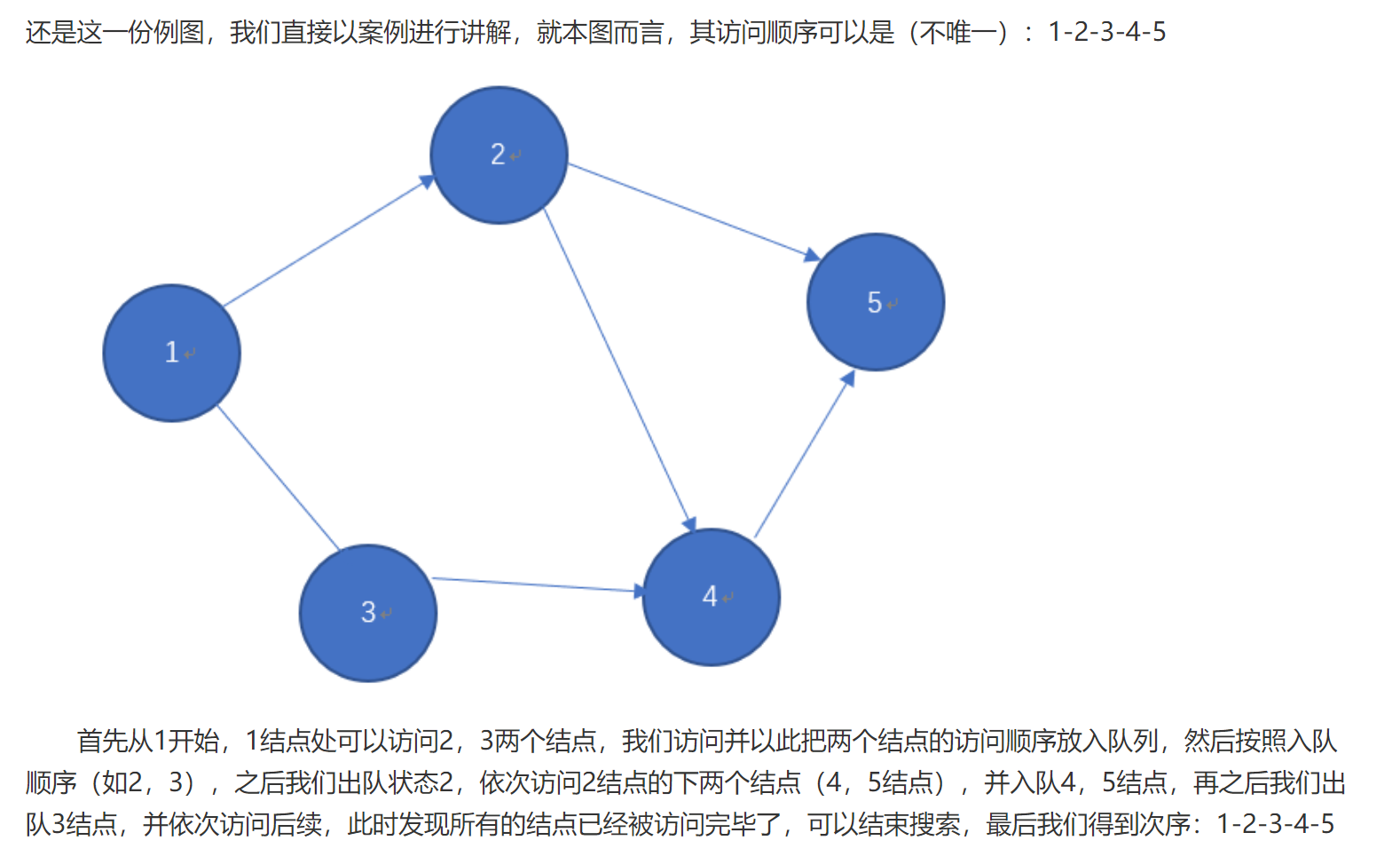
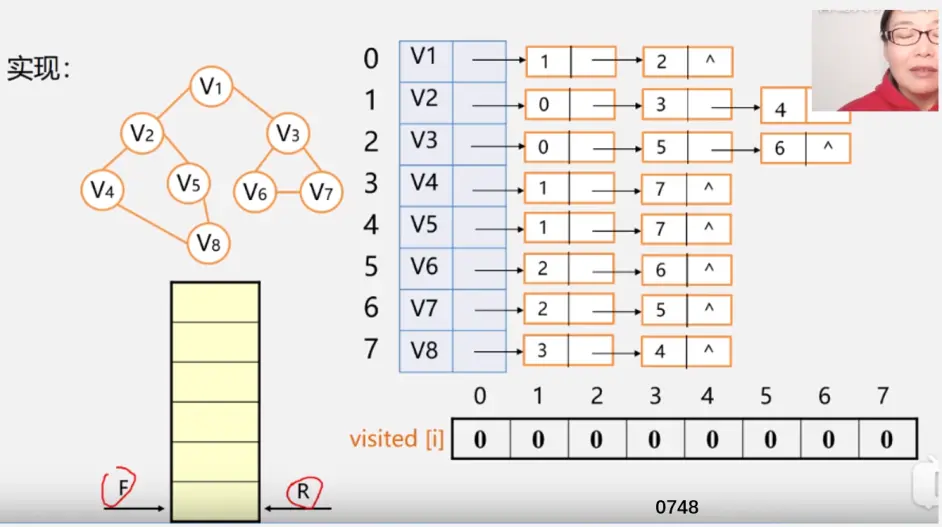
Similar to the hierarchical traversal of the tree (use the queue root node to queue up its left and right children...) set the starting point as v1, Queue 0 at position 0 in the array – "after V1 is accessed, it is necessary to modify visited[1]=1 to queue the unreachable adjacency points of V1 and queue 1 and 2 –" after V2 is accessed, it is necessary to modify visited[2]=1 to queue the unreachable adjacency points of V2 (3 and 4) – "V3 (current queue head) after accessing, it is necessary to modify visited[1]=1... (the queue is empty, and the visit array is 1. The traversal ends)

Algorithm implementation

BFS The template code is as follows:

/**
 * Return appropriate retrieval data
 */
int BFS(Node root, Node target) 
{
    Queue<Node> queue;  //Create queue
    int step = 0;       // Step point of the current queue
    // initialize
    add root to queue;
    // BFS
    while (queue is not empty) 
    {
        step = step + 1;
        //The number of steps increases gradually
        int size = queue.size();
        for (int i = 0; i < size; ++i) 
        {
            Node cur = the first node in queue;
            if cur is target
                return step - 1;
            for (Node next : the neighbors of cur) 
            {//A two-dimensional direction array is often used here
                add next to queue;
            }
            remove the first node from queue;
        }
    }
    return -1;          //Error return value
}
Also provide a copy BFS The core of the code is memory BFS The following code is for reference only

void BFSL(int pos,pGraph G,int visited[30])//Breadth first traversal of undirected graph from pos point
{
    int queue[G->Vnum];//Queue assisted BFS traversal
    int head=0,tail=0;//Head and tail pointer
    Arcnode* p;
    queue[tail]=pos;
    visited[pos]=1;//Mark traversed
    tail++;
    while(head!=tail)
    {
        pos=queue[head];//Out of line operation
        head++;
        printf("%d ",pos);
        p=G->vertice[pos].firstarc;
        while(p!=NULL)
        {
            if(visited[p->adjvex]==0)//Judge whether it has been traversed
            {
                queue[tail]=p->adjvex;//Queue operation
                visited[p->adjvex]=1;//Mark traversed
                tail++;
            }
            p=p->next;
        }
    }
}

compare