Given an integer array without duplicate elements, {nums. A maximum binary tree constructed directly and recursively from this array is defined as follows:

1. The root of the binary tree is the largest element in the array {nums}.
2. The left subtree is the largest binary tree constructed recursively through the left part of the maximum value in the array.
3. The right subtree is the largest binary tree constructed recursively through the part on the right of the ， maximum value in the array.

Returns the largest binary tree constructed with the given array {num}.

Example 1:

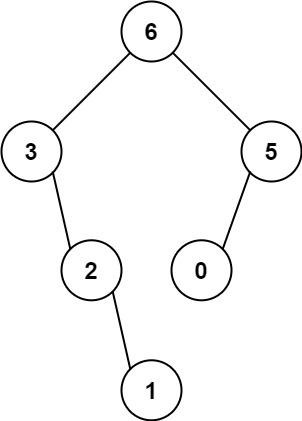
Input: num = [3,2,1,6,0,5]
Output: [6,3,5,null,2,0,null,null,1]
Explanation: recursive calls are as follows:
-The maximum value in [3,2,1,6,0,5] is 6, the left part is [3,2,1], and the right part is [0,5].
    -The maximum value in [3,2,1] is 3, the left part is [], and the right part is [2,1].
        -Empty array, no child nodes.
        -The maximum value in [2,1] is 2, the left part is [], and the right part is [1].
            -Empty array, no child nodes.
            -There is only one element, so the child node is a node with a value of 1.
    -The maximum value in [0,5] is 5, the left part is [0], and the right part is [].
        -There is only one element, so the child node is a node with a value of 0.
        -Empty array, no child nodes.

Example 2:

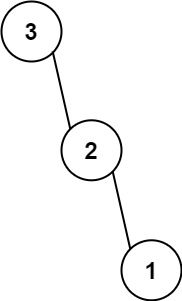
Input: num = [3,2,1]
Output: [3,null,2,null,1]

Tips:

• 1 <= nums.length <= 1000
• 0 <= nums[i] <= 1000
• All integers ， in num ， are different from each other

 1 /**
 2  * Definition for a binary tree node.
 3  * public class TreeNode {
 4  *     int val;
 5  *     TreeNode left;
 6  *     TreeNode right;
 7  *     TreeNode() {}
 8  *     TreeNode(int val) { this.val = val; }
 9  *     TreeNode(int val, TreeNode left, TreeNode right) {
10  *         this.val = val;
11  *         this.left = left;
12  *         this.right = right;
13  *     }
14  * }
15  */
16 class Solution {
17     public TreeNode constructMaximumBinaryTree(int[] nums) {
18         return construct(nums,0,nums.length-1);
19     }
20 
21     public TreeNode construct(int[] nums,int l,int r){
22         if (l>r) return null;
23         int max=-1,index=-1;
24         for (int i=l;i<=r;i++){
25             if (nums[i]>max){
26                 max=nums[i];
27                 index=i;
28             }
29         }
30         TreeNode head=new TreeNode(max);
31         head.left=construct(nums,l,index-1);
32         head.right=construct(nums,index+1,r);
33         return head;
34     }
35 }

Idea: traverse to find the maximum value, record the index and maximum value, create a new header node, and then recursively call to generate the left subtree and right subtree.

Topic 2:

Given the preorder and inorder of a tree. Construct a binary tree and return its root node.

 

Example 1:

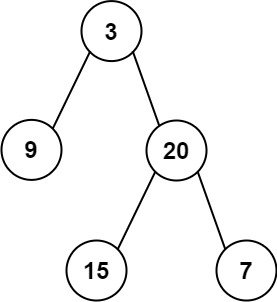
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]

Example 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

 

Tips:

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• Neither preorder nor inorder has duplicate elements
• inorder ， all appear in ， preorder
• Preorder is guaranteed to be the preorder traversal sequence of binary tree
• inorder # is guaranteed to be a middle order traversal sequence of a binary tree

 1 /**
 2  * Definition for a binary tree node.
 3  * public class TreeNode {
 4  *     int val;
 5  *     TreeNode left;
 6  *     TreeNode right;
 7  *     TreeNode() {}
 8  *     TreeNode(int val) { this.val = val; }
 9  *     TreeNode(int val, TreeNode left, TreeNode right) {
10  *         this.val = val;
11  *         this.left = left;
12  *         this.right = right;
13  *     }
14  * }
15  */
16 class Solution {
17     public TreeNode buildTree(int[] preorder, int[] inorder) {
18         return build(preorder,0,preorder.length-1,inorder,0,inorder.length-1);
19     }
20 
21     public TreeNode build(int[] preorder,int l1,int r1,int[] inorder,int l2,int r2){
22         if (l1>r1||l2>r2) return null;
23         TreeNode root=new TreeNode(preorder[l1]);
24         int index=-1;
25         for (int i=l2;i<=r2;i++){
26             if (inorder[i]==preorder[l1]){
27                 index=i;
28                 break;
29             }
30         }
31         root.left=build(preorder,l1+1,l1+index-l2,inorder,l2,index-1);
32         root.right=build(preorder,l1+index-l2+1,r1,inorder,index+1,r2);
33         return root;
34     }
35 }

Idea: the root node can be known according to the pre order traversal, while in the middle order traversal, the left and right are the composition of the left subtree and the right subtree respectively.

Question 3:

106. Construct binary tree from middle order and post order traversal sequenceslabuladong problem solutionthinking

According to the middle order traversal and post order traversal of a tree, a binary tree is constructed.

be careful:
You can assume that there are no duplicate elements in the tree.

For example, give

Middle order traversal inorder = [9,3,15,20,7]
Postorder traversal postorder = [9,15,7,20,3]

Return the following binary tree:

    3
   / \
  9  20
    /  \
   15   7

 1 /**
 2  * Definition for a binary tree node.
 3  * public class TreeNode {
 4  *     int val;
 5  *     TreeNode left;
 6  *     TreeNode right;
 7  *     TreeNode() {}
 8  *     TreeNode(int val) { this.val = val; }
 9  *     TreeNode(int val, TreeNode left, TreeNode right) {
10  *         this.val = val;
11  *         this.left = left;
12  *         this.right = right;
13  *     }
14  * }
15  */
16 class Solution {
17     public TreeNode buildTree(int[] inorder, int[] postorder) {
18         return build(inorder,0,inorder.length-1,postorder,0,postorder.length-1);
19     }
20     public TreeNode build(int[] inorder,int l1,int r1,int[] postorder,int l2,int r2){
21         if (l1>r1||l2>r2) return null;
22         TreeNode root=new TreeNode(postorder[r2]);
23         int index=-1;
24         for (int i=l1;i<=r1;i++){
25             if (inorder[i]==postorder[r2]){
26                 index=i;
27                 break;
28             }
29         }
30         root.left=build(inorder,l1,index-1,postorder,l2 ,r2-r1+index-1);
31         root.right=build(inorder,index+1,r1,postorder,r2-r1+index ,r2-1);
32         return root;
33     }
34 }

Idea: similar to question 2, the difference is that the root node is the last node.