link
subject
Give you an integer array nums. In nums, the range of subarray is the difference between the largest element and the smallest element in the subarray.
Returns the sum of all subarray ranges in num.
A subarray is a sequence of consecutive non empty elements in an array.
Examples
Example 1:
Input: num = [1,2,3]
Output: 4
Explanation: the six subarrays of nums are as follows:
[1] , range = max min = 1 - 1 = 0
[2] , range = 2 - 2 = 0
[3] , range = 3 - 3 = 0
[1,2], range = 2 - 1 = 1
[2,3], range = 3 - 2 = 1
[1,2,3], range = 3 - 1 = 2
The sum of all ranges is 0 + 0 + 0 + 1 + 1 + 2 = 4
Example 2:
Input: num = [1,3,3]
Output: 4
Explanation: the six subarrays of nums are as follows:
[1] , range = max min = 1 - 1 = 0
[3] , range = 3 - 3 = 0
[3] , range = 3 - 3 = 0
[1,3], range = 3 - 1 = 2
[3,3], range = 3 - 3 = 0
[1,3,3], range = 3 - 1 = 2
The sum of all ranges is 0 + 0 + 0 + 2 + 0 + 2 = 4
Example 3:
Input: num = [4, - 2, - 3,4,1]
Output: 59
Explanation: the sum of all subarray ranges in num is 59
explain
- 1 <= nums.length <= 1000
- -10e9 <= nums[i] <= 10e9
Advanced
Design a solution with time complexity of ^ O(n)
Idea 1 (violence)
We can enumerate the left and right subscripts of each subarray, count the difference between the maximum and minimum values of each subarray in turn, and accumulate them.
C++ Code
class Solution {
public:
long long subArrayRanges(vector<int>& nums) {
//Violence: two-layer for loop enumerating left and right boundaries [i,j]
long long sum=0;
for(int i=0;i<nums.size();i++)
{
int Max=nums[i], Min=nums[i];
for(int j=i;j<nums.size();j++)
{
Max=max(Max,nums[j]);
Min=min(Min,nums[j]);
sum+=Max-Min;
}
}
return sum;
}
};Idea 2 (monotone stack)
The problem is to find the range sum of the subarray (the sum of the difference between the maximum and minimum values of all subarrays). We can convert it to the sum of the maximum values of all subarrays minus the sum of the minimum values of all subarrays.
If the maximum value of N subarrays is A[i], then the contribution of A[i] element to sum is n*A[i]. Similarly, if the maximum value of m subarrays is A[j], then the contribution of A[j] element to sum is - m*A[j].
How to find this n? Let's take the maximum value of N subarray as A[i] as an example. When finding A[i] as the maximum value to contribute to sum, the solution of this n: find the first number A[left] on the left and the first number A[right] on the right of A[i], that is, find the longest continuous subarray with A[i] as the maximum value, Here, the number of all subarrays including A[i] is (i-left)*(right-i), and the total contribution is (i-left)*(right-i)*A[i]. For example, for element 3 with subscript i=4 in [0,4,2,1,3,2,1,4,0], left is 4 with subscript 1 and right is 4 with subscript 7. The number of subarrays containing A[i] is (4-1) * (7-4) = 9, The contribution of A[i] as the maximum value to sum is A[i]*9=3*9=27. Similarly, we can find out the contribution of each element as the maximum value to sum and the contribution of each element as the minimum value to sum.
As for how to find the first element greater than or less than A[i] to the left or right? This requires a monotonic stack. We preprocess the arrays minLeft, minRight, maxLeft and maxRight with monotonically increasing stack, where minLeft[i] represents the subscript of the nearest number smaller than it on the left side of num [i], and minRight[i] represents the subscript of the nearest number smaller than it on the right side of num [I]. The same is true for others, so that our final sum can be calculated directly:
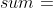
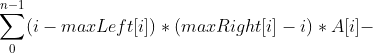
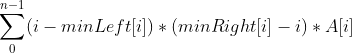
Then the problem comes again. How to preprocess the arrays minLeft, minRight, maxLeft and maxRight through the monotone stack? Taking minLeft as an example, traverse the entire array nums from left to right. When processing to nums[i], perform the out of stack operation until the stack is empty or the number in nums with the top element as the subscript is logically less than nums[i]. If the stack is empty, minLeft[i] = − 1, otherwise minLeft[i] is equal to the top element of the stack, and then put the subscript i into the stack.
Here, the logical less than is defined as: if nums[i]=nums[j], the logical size of nums[i] and nums[j] is determined by the logical size of subscript i and subscript j, that is, if I < J, nums[i] is logically less than nums[j].
C++ Code
class Solution {
public:
long long subArrayRanges(vector<int>& nums) {
int n = nums.size();
vector<int> minLeft(n), minRight(n), maxLeft(n), maxRight(n);
stack<int> minStack, maxStack;
for (int i = 0; i < n; i++) {
while (!minStack.empty() && nums[minStack.top()] > nums[i]) {
minStack.pop();
}
minLeft[i] = minStack.empty() ? -1 : minStack.top();
minStack.push(i);
// If num [maxstack. Top()] = = num [i], then by definition,
// nums[maxStack.top()] is logically less than nums[i], because maxstack top() < i
while (!maxStack.empty() && nums[maxStack.top()] <= nums[i]) {
maxStack.pop();
}
maxLeft[i] = maxStack.empty() ? -1 : maxStack.top();
maxStack.push(i);
}
minStack = stack<int>();
maxStack = stack<int>();
for (int i = n - 1; i >= 0; i--) {
// If num [minstack. Top()] = = num [i], by definition,
// Num [minstack. Top()] is logically greater than num [i] because minstack top() > i
while (!minStack.empty() && nums[minStack.top()] >= nums[i]) {
minStack.pop();
}
minRight[i] = minStack.empty() ? n : minStack.top();
minStack.push(i);
while (!maxStack.empty() && nums[maxStack.top()] < nums[i]) {
maxStack.pop();
}
maxRight[i] = maxStack.empty() ? n : maxStack.top();
maxStack.push(i);
}
long long sumMax = 0, sumMin = 0;
for (int i = 0; i < n; i++) {
sumMax += static_cast<long long>(maxRight[i] - i) * (i - maxLeft[i]) * nums[i];
sumMin += static_cast<long long>(minRight[i] - i) * (i - minLeft[i]) * nums[i];
}
return sumMax - sumMin;
}
};