1. Dynamic planning

The dynamic programming algorithm is similar to the divide and conquer method. Its basic idea is to decompose the problem to be solved into several sub problems. First solve the sub problems, and then get the solution of the original problem from the solutions of these sub problems. Different from the divide and conquer method, the sub problems obtained by decomposition are often not independent of each other. If the divide and conquer method is used to solve this kind of problem, the number of sub problems obtained by decomposition is too large, so that it takes exponential time to finally solve the original problem. However, the number of different subproblems is often only polynomial. When using divide and conquer method, some subproblems are repeatedly calculated many times. If you can save the answers of the solved sub questions and find the obtained answers when necessary, you can
To avoid a large number of repeated calculations, so as to obtain the polynomial time algorithm. In order to achieve this goal, a table can be used to record the answers of all solved sub questions. No matter whether the sub problem will be used in the future, as long as it has been calculated, the results will be filled in the table. This is the basic idea of dynamic programming. There are many specific dynamic programming algorithms, but they have the same filling format.
Dynamic programming algorithm is suitable for solving optimization problems. Generally, the dynamic programming algorithm can be designed according to the following steps:
(1) Find out the properties of the optimal solution and characterize its structural characteristics

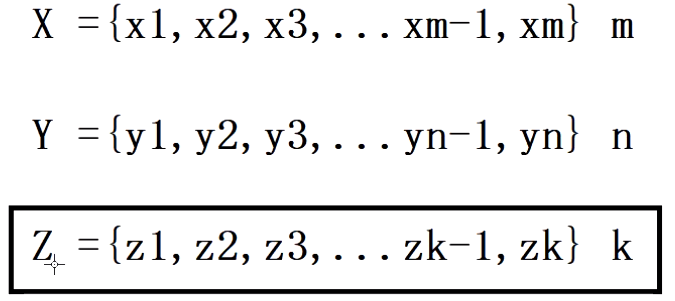
(2) Define the optimal value recursively
(3) The optimal value is calculated in a bottom-up manner
(4) According to the information obtained when calculating the optimal value, the optimal solution is constructed
Steps (1) to (3) are the basic steps of the dynamic programming algorithm. In the case where only the optimal value needs to be found, step (4) can be omitted. If the optimal solution is required, step 4 must be performed. At this time, when calculating the optimal value in step (3), it is usually necessary to record more information, so that in step (4), the optimal solution can be quickly constructed according to the recorded information

2. Divide and conquer strategy will not be solved repeatedly, but dynamic programming may be solved repeatedly

3. Longest common subsequence

For example, sequence X = {A,B,C,B,D,A,B}; Corresponding to 1,2,3,4,5,6,7 subscripts respectively, the sequence Y = {A,C,D,B} is its subsequence, and the corresponding increasing subscript sequence is {1,3,5,7}, while the sequence Z = {A,D,C,A} is not its subsequence, because the corresponding subscript sequence of Z is {1,5,3,6}, it is not an increasing subscript sequence

When x and Z are two subsequences of a given subsequence, the other subsequence is the subsequence of X and Z

For example, if X=(A,B,C,B,D,A,B}, Y={B,D,C,A,B,A), sequence {B,C,A) is a common subsequence of X and y, but it is not the longest common subsequence of X and Y. sequence {B,C,B,A} is also a common subsequence of X and y, its length is 4, and it is the longest common subsequence of X and y, because X and y have no common subsequence with a length greater than 4

Longest common subsequence problem: given two sequences X = {x1,x2,x3,..., xm} and Y = {y1,y2,y3,..., yn}, find the longest common subsequence of X and y

Dynamic programming algorithm can effectively solve this problem. Next, an effective algorithm to solve this problem is designed according to each step of dynamic programming algorithm design

4. Algorithm idea
① If xm == yn, then xm == yn == zk, then ZK-1 = XM-1 & & yn-1
If the last element of the X sequence is equal to the last element of the Y sequence, then the last element of the X sequence and the last element of the Y sequence are equal to the last element of the longest common subsequence, then delete the last element of the X sequence and the Y sequence to reduce the scale of the problem

② If XM= yn，xm != zk, then ZK = XM-1 & & YN
If the last element of X sequence is neither equal to the last element of Y sequence nor the last element of the longest common subsequence, delete the last element of X sequence to reduce the scale of the problem

③ If yn= xm，yn != zk, then ZK = XM & & yn-1
If the last element of Y sequence is neither equal to the last element of X sequence nor the last element of the longest common subsequence, delete the last element of Y sequence to reduce the scale of the problem

c[m][n] represents the longest common subsequence, m represents the length of X sequence, and N represents the length of Y sequence

If the size of m is 0 or the size of n is 0, the length of the longest common subsequence is also 0

If xm == yn, the longest common subsequence becomes c[m-1][n-1]+1. Note that it must be + 1

If XM= YN, then the longest common subsequence is Max(c[m-1][n],c[m][n-1])

5. Longest common subsequence code (recursive)

One problem with the following code is that it is solved repeatedly when calculating max1 and max2, which leads to very high time complexity

int LCSLength(const char* X, const char* Y, int m, int n)
{
	if (m == 0 || n == 0) return 0;
	else
	{
		if (X[m] == Y[n])
		{
			return LCSLength(X, Y, m - 1, n - 1) + 1;
		}
		else
		{
			int max1 = LCSLength(X, Y, m - 1, n);
			int max2 = LCSLength(X, Y, m, n - 1);
			return max1 > max2 ? max1 : max2;
		}
	}
}
int main()
{
	char X[] = { "#ABCBDAB" };
	//            01234567 subscript
	char Y[] = { "#BDCABA" };
	//            0123456 subscript
	int xm = strlen(X) - 1;
	int yn = strlen(Y) - 1;
	int maxlen = LCSLength(X, Y, xm, yn);
	cout << maxlen << endl;

	return 0;
}

6. Code optimization of the longest common subsequence (recursive method)

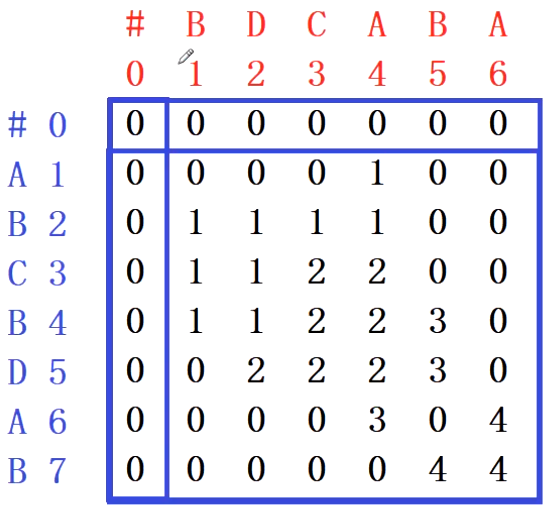
Direction table

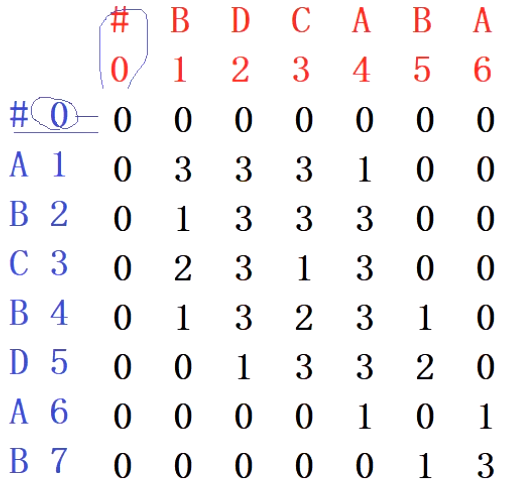
In the direction table, the diagonal indicates 1, 2 when going up and 3 when going left

template<class T>
void Print_Vec(vector<vector<T>>& c)
{
	int m = c.size();
	for (int i = 0; i < m; ++i)
	{
		int n = c[i].size();
		for (int j = 0; j < n; ++j)
		{
			cout << setw(3) << c[i][j];
		}
		cout << endl;
	}
	cout << endl;
}
int LCSLength(const char* X, const char* Y, int m, int n, vector<vector<int>>& c, vector<vector<int>>& s)
{
	if (m == 0 || n == 0) return 0;
	else if (c[m][n] != 0) return c[m][n];
	else
	{
		if (X[m] == Y[n])
		{
			c[m][n] =  LCSLength(X, Y, m - 1, n - 1, c, s) + 1;
			s[m][n] = 1;
		}
		else
		{
			int max1 = LCSLength(X, Y, m - 1, n, c, s);
			int max2 = LCSLength(X, Y, m, n - 1, c, s);
			if (max1 > max2)
			{
				c[m][n] = max1;
				s[m][n] = 2;
			}
			else
			{
				c[m][n] = max2;
				s[m][n] = 3;
			}
		}
	}
	return c[m][n];
}
void LCS(const char* X, vector<vector<int>>& s, int i, int j)
{
	if (i == 0 || j == 0) return;
	if (s[i][j] == 1)
	{
		LCS(X, s, i - 1, j - 1);
		cout << X[i];
	}
	else if (s[i][j] == 2)
	{
		LCS(X, s, i - 1, j);
	}
	else
	{
		LCS(X, s, i, j - 1);
	}
}
int main()
{
	char X[] = { "#ABCBDAB" };
	//            01234567 subscript
	char Y[] = { "#BDCABA" };
	//            0123456 subscript
	int xm = strlen(X) - 1;
	int yn = strlen(Y) - 1;
	//Define two-dimensional arrays in C + +
	vector<vector<int>> c;
	vector<vector<int>> s;//Direction table
	c.resize(xm + 1);//Reset the size of 7 grids, and each grid is of vector < int > type
	s.resize(xm + 1);
	for (int i = 0; i < xm + 1; ++i)//Loop initializes each grid
	{
		c[i].resize(yn + 1,0);
		s[i].resize(yn + 1,0);//Initialize direction table
	}

	int maxlen = LCSLength(X, Y, xm, yn, c, s);
	Print_Vec(c);
	Print_Vec(s);
	cout << maxlen << endl;
	LCS(X, s, xm, yn);

	return 0;
}

6. Code optimization of the longest common subsequence (non recursive)