6. 2-3-4 tree efficiency
Through the previous introduction, we know that in a binary tree, each node has only one data item and at most two child nodes. If each node is allowed to have more data items and more child nodes, it is a multi fork tree. In this blog, we will introduce the 2-3-4 tree, which is a multi fork tree. Each node has up to four child nodes and three data items.
Text:
1. 2-3-4 tree introduction
Each node of the 2-3-4 tree has at most four word nodes and three data items. The number of 2,3,4 in the name refers to the number of child nodes that a node may contain. There are three possible scenarios for non leaf nodes:
① . a node with one data item always has two child nodes;
② . a node with two data items always has three child nodes;
③ . a node with three data items always has four child nodes;
In short, the number of child nodes of a non leaf node is always 1 more than the data items it contains. If the number of child nodes is L and the number of data items is D, then: L = D + 1
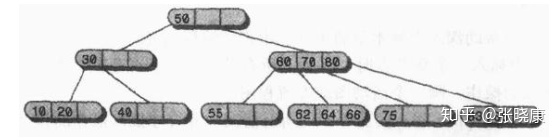
A leaf node (the bottom row in the figure above) has no child nodes, but it may contain one, two or three data items. An empty node will not exist.
A very important point in the tree structure is the relationship between key values of nodes. In a binary tree, all nodes whose keyword value is smaller than that of a node are on the subtree whose left child node is the root; All nodes whose keyword value is greater than the value of a node are on the subtree whose right child node is the root. The 2-3-4 tree rule is the same, and the following points are added:
For convenience of description, numbers from 0 to 2 are used to number data items and numbers from 0 to 3 are used to number child nodes, as shown in the following figure:
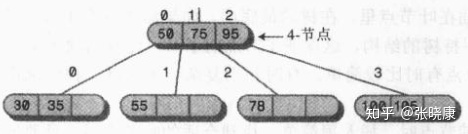
① . the keyword value of all child nodes whose root is a child tree of child0 is less than key0;
② . the keyword value of all child nodes of the subtree whose root is child1 is greater than key0 and less than key1;
③ . the keyword value of all child nodes of the subtree whose root is child2 is greater than key1 and less than key2;
④ The keyword value of all child nodes whose root is child3 is greater than key2.
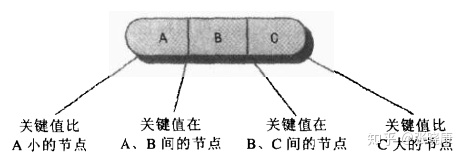
The simplified relationship is shown in the figure below. Since duplicate key values are generally not allowed in the 2-3-4 tree, it is not necessary to consider the same comparison key values.
2. Search 2-3-4 tree
Finding data items with specific keyword values is similar to searching in a binary tree. Start the search from the root node. Unless the keyword value is the root, select the appropriate range of keyword values and turn to that direction until it is found.
For example, for the following figure, we need to find the data item with the keyword value of 64.
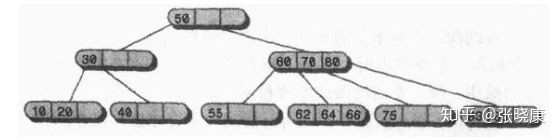
First, start from the root node. The root node has only one data item 50, which is not found. Moreover, because 64 is larger than 50, go to Child1, the child node of the root node. 60 | 70 | 80 was not found, and 60 < 64 < 70, so we still found child1,62|64|66 of the node. We found that the second data item was exactly 64, so we found it.
3. Insert
New data items are usually inserted in leaf nodes, at the bottom of the tree. If you insert a node with child nodes, the number of child nodes will change to maintain the tree structure, because in the 2-3-4 tree, the child nodes of the node are 1 more than the data items.
Insertion is sometimes simple, but sometimes complex.
① . it is very simple to insert a node without full data items. To find the appropriate location, you only need to insert a new data item. Insertion may involve moving one or two other data items in a node, so that the keyword values remain in the correct order after the new data item is inserted. As shown below:
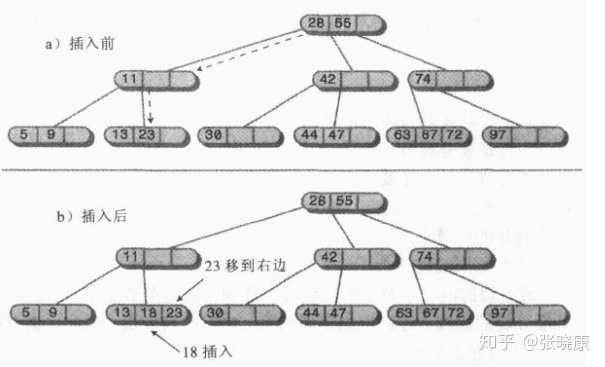
② . if the node is full on the way down to find the insertion location, the insertion becomes complex. In this case, the node must be split, which can ensure the balance of 2-3-4 tree.
ps: the top-down 2-3-4 tree is discussed here, because the node splits on the way down to find the insertion point. Set the data items to be split as a, B and C. The following is the case of node splitting (assuming that the split node is not the root node):
1. Node splitting
1. Create a new empty node, which is the brother of the node to be split, on the right side of the node to be split;
2, Move data item C to the new node;
3, Move data item B to the parent node of the node to be split;
4, Data item A remains in its original position;
5, The two rightmost child nodes are disconnected from the place to be split and connected to the new node.
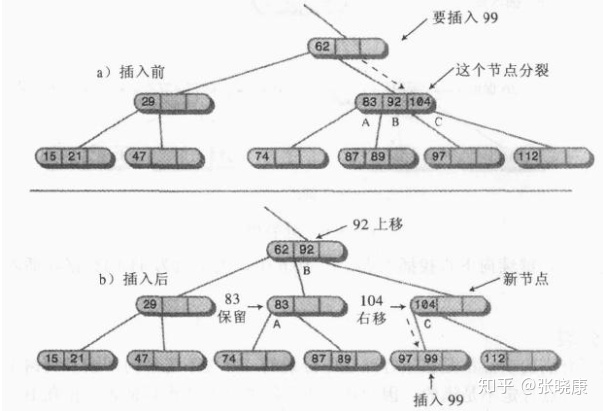
The above figure describes an example of node splitting. Another way to describe node splitting is that a 4-node becomes two 2-nodes. Node splitting is to move data up and right, so as to maintain the balance of numbers. Generally, only one node needs to be split for insertion, unless there is more than one full node on the insertion path, which requires multiple splitting.
2. Root division
If you encounter a full root node at the beginning of finding the insertion node, the insertion process is more complex:
① Create a new root node, which is the parent node of the node to be split.
② Create a second new node, which is the brother node of the node to be split;
③ . move data item C to a new sibling node;
④ . move data item B to the new root node;
⑤ . data item A remains in its original position;
⑥ . disconnect the two rightmost child nodes of the split node and connect them to the new sibling node.
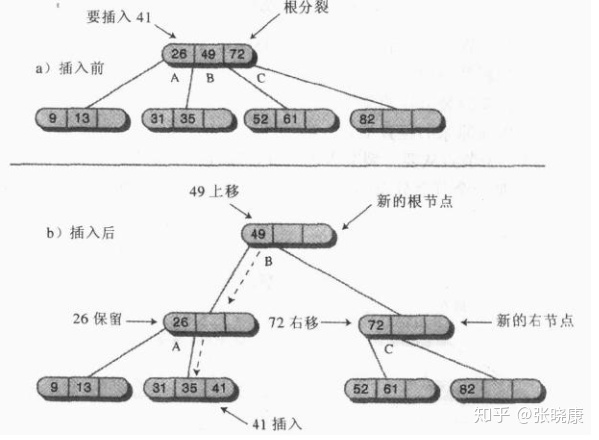
The above figure shows the root splitting. After splitting, the height of the whole tree is increased by 1. Another way to describe root splitting is to say that 4-nodes become three 2-nodes.
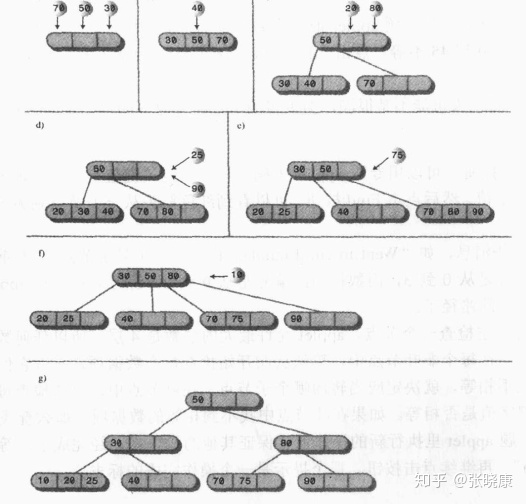
Note: when inserting a node that is not full, continue to look down for its child nodes for insertion. If the node is directly inserted, the number of child nodes must be increased, because the number of child nodes of the node in the 2-3-4 tree is 1 more than the data item; If the inserted nodes are full, node splitting is required. The following figure shows a series of insertion processes. Four nodes are split, two are root and two are leaf nodes:
4. Complete source code implementation
It is divided into Node class, which represents the data item class DataItem of each Node, and the last 2-3-4 tree class tree234 class
package tree;
import java.util.LinkedList;
import java.util.Queue;
public class Tree234 {
private Node root = new Node();
//test
public static void main(String[] args) {
Tree234 tree = new Tree234();
int[] a = new int[] { 70, 50, 30, 40, 20, 80, 25, 90, 75, 10 };
for (int i = 0; i < a.length; i++) {
tree.insert(a[i]);
}
System.out.print("root Node data:");
tree.root.displayNode();
tree.display(tree.root);
// System.out.println(tree.find(75));
}
// Find keyword value
public int find(long key) {
Node curNode = root;
int childNum;
while (true) {
if ((childNum = curNode.findItem(key)) != -1) {
return childNum;
} else if (curNode.isLeaf()) {
return -1;
} else {
// Find next node
curNode = getNextChild(curNode, key);
}
}
}
// insert
public void insert(long dvalue) {
Node cuNode = root;
DataItem tempItem = new DataItem(dvalue);
while (true) {
if (cuNode.isFull()) {
split(cuNode);
cuNode = cuNode.getParent();
cuNode = getNextChild(cuNode, dvalue);
} else if (cuNode.isLeaf()) {
break;
} else {
cuNode = getNextChild(cuNode, dvalue);
}
}
cuNode.insertItem(tempItem);
}
// division
public void split(Node thisNode) {
DataItem itemB, itemC;
Node parent, child2, child3;
itemC = thisNode.removeItem();
itemB = thisNode.removeItem();
child2 = thisNode.disconnectChild(2);
child3 = thisNode.disconnectChild(3);
Node newright = new Node();
// Judge whether it is the root node
if (thisNode == root) {
root = new Node();
parent = root;
root.connectChild(0, thisNode);
} else {
parent = thisNode.getParent();
}
// The parent node will add a data item, so the child position under the parent node needs to be changed, only for the left
int index = parent.insertItem(itemB);
int n = parent.getItemNum();
for (int i = n - 1; i > index; i--) {
Node temp = parent.disconnectChild(i);
parent.connectChild(i + 1, temp);
}
parent.connectChild(index + 1, newright);
newright.insertItem(itemC);
// Note that when the root node data item is full, not when the leaf node is full
newright.connectChild(0, child2);
newright.connectChild(1, child3);
}
// Get the next node
public Node getNextChild(Node theNode, long value) {
if (theNode == null) {
System.out.println("empty error");
}
int i;
for (i = 0; i < theNode.getItemNum(); i++) {
if (value < theNode.getItem(i).dData) {
return theNode.getChild(i);
}
}
return theNode.getChild(i);
}
// Print
public void display(Node node) {
Queue<Node> queue = new LinkedList<Node>();
queue.add(root);
int level = 0;
while (!queue.isEmpty()) {
level++;
int size = queue.size();
for (int i = 0; i < size; i++) {
Node temp = queue.remove();
System.out.println("level:" + level + "\t" + "child:" + i);
temp.displayNode();
for (int j = 0; j < temp.childArray.length; j++) {
if (temp.getChild(j) != null) {
queue.add(temp.getChild(j));
}
}
}
}
}
// data item
class DataItem {
public long dData;
public DataItem(long data) {
this.dData = data;
}
public void displayItem() {
System.out.print(" " + dData);
}
}
//node
class Node {
private static final int ORDER = 4;
private int numItems; // Number of data items
private Node parent; // Parent node
private Node[] childArray = new Node[ORDER];// An array that stores child nodes
private DataItem[] itemArray = new DataItem[ORDER - 1];// An array that stores data items
// Connect child nodes
public void connectChild(int childNum, Node child) {
childArray[childNum] = child;
if (child != null) {
child.parent = this;
}
}
// Disconnect node
public Node disconnectChild(int childNum) {
Node tempNode = childArray[childNum];
childArray[childNum] = null;
return tempNode;
}
// Get a child node
public Node getChild(int childNum) {
return childArray[childNum];
}
// Get parent node
public Node getParent() {
return parent;
}
// Judge whether it is a leaf node
public boolean isLeaf() {
return (childArray[0] == null) ? true : false;
}
// Get a data item of the node
public DataItem getItem(int index) {
return itemArray[index];
}
// Get the number of node data items
public int getItemNum() {
return numItems;
}
// Judge whether the data item of the node is full
public boolean isFull() {
return (numItems == ORDER - 1) ? true : false;
}
// Insert data item
public int insertItem(DataItem newItem) {
int i;
long key = newItem.dData;
numItems++;
for (i = ORDER - 2; i >= 0; i--) {
if (itemArray[i] == null)
continue;
long oldKey = itemArray[i].dData;
if (oldKey > key) {
itemArray[i + 1] = itemArray[i];
} else if (oldKey < key) {
itemArray[i + 1] = newItem;
return i + 1;
}
}
itemArray[0] = newItem;
return 0;
}
// Find the location of the data item in the node
public int findItem(long key) {
for (int i = 0; i < itemArray.length; i++) {
if (itemArray[i] == null)
break;
if (itemArray[i].dData == key)
return i;
}
return -1;
}
// Remove data item
public DataItem removeItem() {
DataItem temp = itemArray[numItems - 1];
itemArray[numItems - 1] = null;
numItems--;
return temp;
}
// Print all data items
public void displayNode() {
for (int i = 0; i < numItems; i++) {
itemArray[i].displayItem();
}
System.out.println("");
}
}
}
Operation screenshot:
The insertion sequence is: 70, 50, 30, 40, 20, 80, 25, 90, 75, 10
The actual insertion is shown in the figure below:
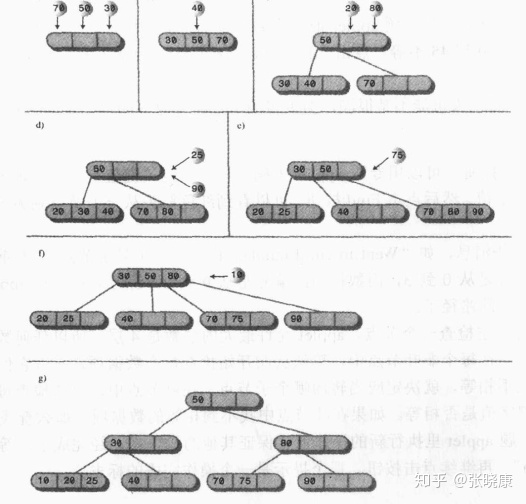
The screenshot of the operation is:

5. 2-3-4 trees and red black trees
2-3-4 trees are multi fork trees, while red and black trees are binary trees. They may look completely different. However, in a sense, they are exactly the same. One can become another by applying some simple rules, and the operation to keep them balanced is the same. Mathematically, they are called isomorphism.
① . corresponding rules
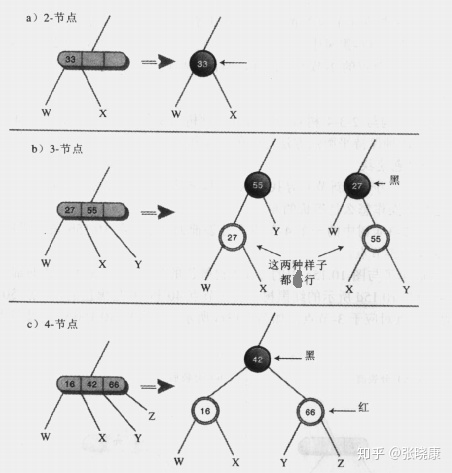
The following three rules can be applied to convert a 2-3-4 tree into a red black tree:
1, Each 2-node in the 2-3-4 tree is transformed into a black node of the red black tree.
2, Each 3-node is transformed into a child node and a parent node. The child node has two own child nodes: W and X or X and Y. The parent node has another child node: Y or w. It doesn't matter which node becomes a child or parent node. Child nodes are painted red and parent nodes are painted black.
3, Each 4- node is transformed into a parent node and two child nodes. The first child node has its own child nodes W and X; The second child node has child nodes Y and Z. As before, the child node is painted red and the parent node is painted black.
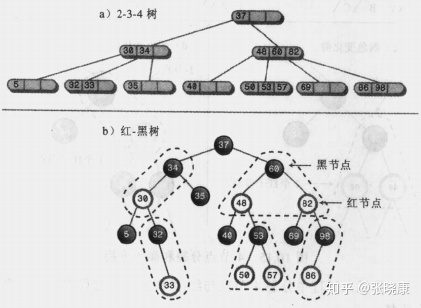
The following figure shows a 2-3-4 tree transformed into a corresponding red black tree. The subtree surrounded by dotted lines is changed from 3-node and 4-node. After conversion, the rules of red black tree are met. The root node is red, and the two red nodes will not be connected. The number of black nodes on each path from root to leaf node is the same.
② . operation equivalence
Not only the structure of red black tree corresponds to 2-3-4 tree, but also the operation of the two trees is the same. 2-3-4 trees are balanced by node splitting, and red black trees are balanced by color transformation and rotation.
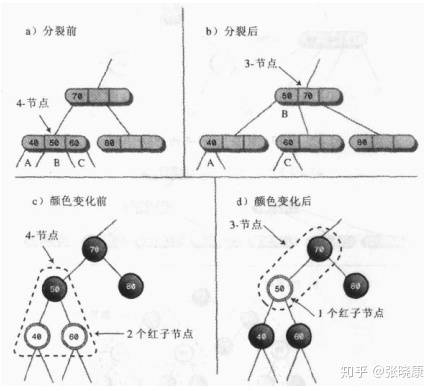
The figure above shows 4-node splitting. The part surrounded by dotted line is equivalent to 4-node. After the color transformation, 40 and 60 nodes are black, and 50 nodes are red. Therefore, node 50 and its parent node 70 are for 3-nodes, as shown by the dotted line in the above figure.
6. 2-3-4 tree efficiency
By analyzing 2-3-4 trees, we can make a comparative analysis with red and black trees. The number of layers of the red black tree (balanced binary tree) is about log2(N+1), while each node of the 2-3-4 tree can have up to 4 data items. If the nodes are full, the height and log4N. Therefore, when all nodes are full, the height of 2-3-4 tree is about half that of red black tree. However, they cannot all be full, so the height of the 2-3-4 tree is roughly log2(N+1) and log2(N+1)/2. Reducing the height of 2-3-4 tree can make its search time shorter than that of red black tree.
On the other hand, each node needs to view more data items, which will increase the search time. Because linear search is used to view data items in nodes, the multiple of search time is directly proportional to M, that is, the average number of data items in each node. The total search time is proportional to M*log4N.