24 point game is a classic card puzzle game.

Common rules of the game:

Remove four cards at A time from poker. Using addition, subtraction, multiplication and division, the first one to get 24 wins. (among them, J stands for 11, Q stands for 12, K stands for 13, A stands for 1), and the 24 point game is solved by programming as required.

Basic requirements: randomly generate four alphanumeric letters representing the playing card, the program automatically lists all possible expressions of 24, and solves the problem with a good language (C/C++/Java or other).

1. Good program style (using custom comment template)

2. The list expression is not duplicate.

Algorithm description:

The core idea of recursive call:

1. Select two numbers in four number traversal;
2. Calculate the result of this combination under this operator;
3. Put the result of step 2 into the ith of the original array and the last into the j of the original array, and assign the corresponding expression to the string array;
4. Call f recursively for the new array, and return if an expression is found;
5. Remove the result of step 2, and put the two numbers in the combination back into the array; the same is true for string array;

C + + source code is as follows:

#include<iostream>
#include<cstdlib>
#include<cmath>
#include<ctime> 
#include<string>
using namespace std;
int n=4;//Triple operation mark value 
int A[4]={0};//Store 4 numbers
char oper[4]={'+','-','*','/'}; //Storage operator
string B[4];
int count=0;
int F(int n){
	//Judge whether three operations have been completed 
	if(n==1){
		if(A[0]==24)//Judge whether the result is 24 
		{	
			cout<<B[0]<<endl;//If it can, the output contains the entire expression in B[0] 
			count++;
		} 
		else
		{} 
	}
	//Any combination of two numbers taken from an array 
	for(int i=0;i<n;i++){
		for(int j=i+1;j<n;j++){
			double a,b;
			string x,y;
			a=A[i];
			b=A[j];
			A[j]=A[n-1];//Assign the last to the empty j 		
			x=B[i];
			y=B[j];
			B[j]=B[n-1];//Put the last digit in the j 
			
			A[i]=a+b;//The first space saves the results of the first two operations 
			B[i]='('+x+'+'+y+')';//Store the result of the first step into the array 
			F(n-1);
			
			//Subtraction should be in order 
			A[i]=a-b;
			B[i]='('+x+'-'+y+')';
			F(n-1);
			A[i]=b-a;
			B[i]='('+y+'-'+x+')';
			F(n-1);
			//multiplication 
			A[i]=a*b;
			B[i]='('+x+'*'+y+')';
			F(n-1);
			//Division should also be in order, and the denominator should not be zero 
			if(b!=0){
				A[i]=a/b;
				B[i]='('+x+'/'+y+')';
				F(n-1);
			}
			if(a!=0){
				A[i]=b/a;
				B[i]='('+y+'/'+x+')';
				F(n-1);
			}
			//When the results of the above four operations cannot meet the conditions
			//In order to enter the next for loop, you need to retrieve the previous i and j values 
			A[i]=a;
			A[j]=b;
			B[i]=x;
			B[j]=y;
		
		}
		
	}
}
/*
*For each class, you can build a random number seed in the constructor once. 
*In this way, because a random number seed will correspond to a random number. Because time is fluctuating, we can update the random number. 
*It can also increase code reuse. Can be said to be a very good programmer thinking. 
*/
class RandomNumber{
public:
    RandomNumber(){
        srand(time(0));
    }
    int get(int begin = 0, int end = 1){
        return rand()%(end-begin+1)+begin;
    }
}; 
int main(){
	RandomNumber r;
    for (int i = 0; i < 4; ++i) {//Generate 4 numbers between 1 and 13 
        A[i]=r.get(1,13);
		cout<<A[i]<<" "; 
    }
    cout<<endl;
	for(int i=0;i<4;i++){
		if(A[i]==1) B[i]='A';
		else if(A[i]==11) B[i]='J';
		else if(A[i]==12) B[i]='Q';
		else if(A[i]==13) B[i]='K';
		else B[i]='0'+A[i];
	} 
	F(n);
	cout<<endl<<"In all "<<count<<" Seed solution"<<endl; 
	return 0;
}

Test results:

 

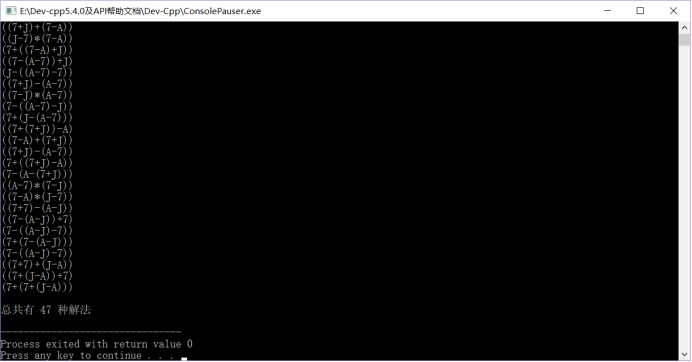
Conclusion:

At the beginning of the 24 o'clock game, considering the parentheses, we arranged these five kinds of games

1.(A*B)*C*D

2.(A*(B*C))*D

3.A*((B*C)*D)

4.A*(B*(C*D))

5.(A*B)*(C*D)

In the beginning, there were too many for loops, and in the end, there were many repetitions, such as A*B and B*A are the same;

Later, I thought of recursion, using n as the number of operations to transfer parameters, each time only two numbers are selected for operation, so I don't need to consider the problem of brackets. The process of writing originally wanted to call another layer of loop to add, subtract, multiply and divide in the double cycle with two numbers in full arrangement. I found that it couldn't be realized. Just Baidu, I found that it was F(n-1) recursion for each operation, and I should also pay attention to it The order of subtraction and division

This assignment gave me a better understanding of the recursive algorithm, which can solve repetitive problems by decomposing a large problem into similar subproblems, so that it can save a lot of trouble compared with the exhaustive method