Dynamic programming problem solving steps
1. Clarify the meaning of dp array subscript and content
2. Determine recurrence formula
3. Array initialization
4. Definite push sequence
5. Verify the formula
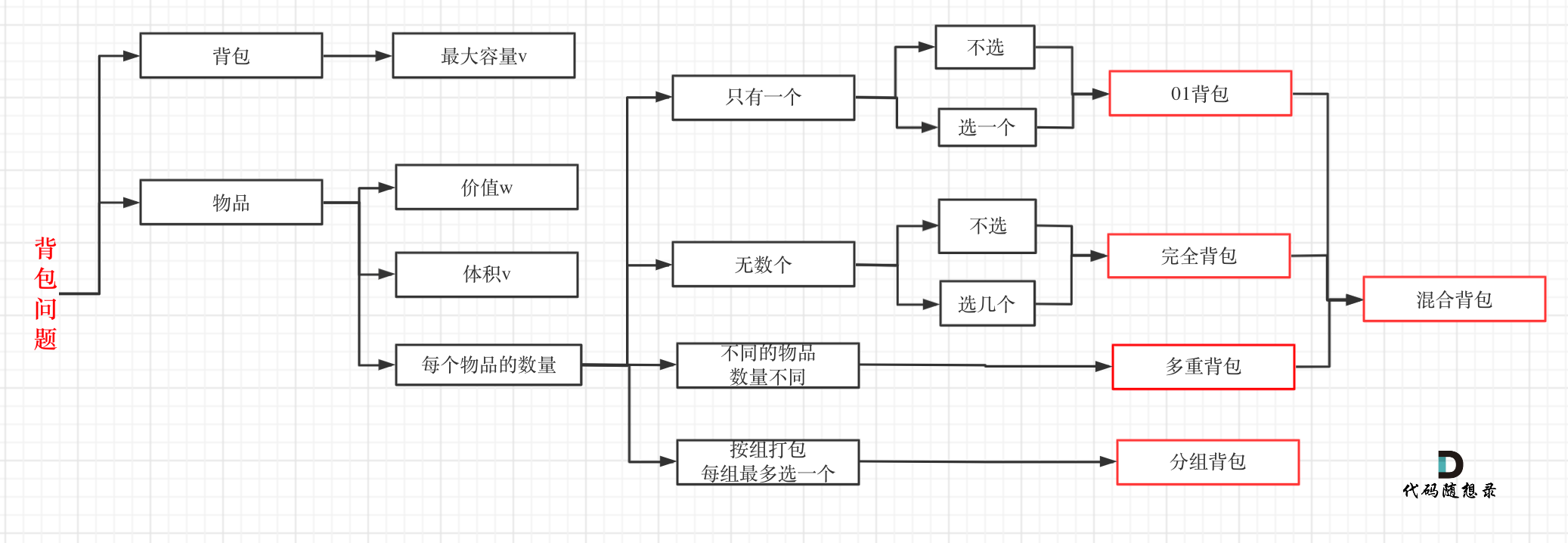
01 Backpack
Recurrence formula:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
j stands for a backpack with a capacity of j, which can hold up to items with a value of dp[j]. When the weight of I exceeds the capacity of j, the value of dp[j] is the same as dp[j-1]. When the weight of I is less than the capacity of j, the maximum value of dp[j] is equal to the capacity of j-i + the value of article i.
initialization:
dp[0] is initialized to 0 because the capacity is 0 and there is no room for items
dp array must take the maximum value when deriving. If the value given by the topic is a positive integer, then the non-0 subscript should be initialized to 0. If the value given by the topic is negative, then the non-0 subscript should be initialized to negative infinity.
Recurrence order:
Positive sequence of external circulation and reverse sequence of internal circulation.
If the internal circulation is in positive order, the items will be repeatedly put in, and the circulation will be from back to front. Each acquisition state will not coincide with the previous acquisition state, so each item will be taken only once
for(int i=0;i<weight.size();i++)
{
for(int j=bagWeight;j>=weight[i];j--)
{
dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);
}
}One dimensional 01 backpack complete code
void test_1_wei_bag_problem() {
vector<int> weight = {1, 3, 4};
vector<int> value = {15, 20, 30};
int bagWeight = 4;
// initialization
vector<int> dp(bagWeight + 1, 0);
for(int i = 0; i < weight.size(); i++) { // Traverse items
for(int j = bagWeight; j >= weight[i]; j--) { // Traversal knapsack capacity
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[bagWeight] << endl;
}
int main() {
test_1_wei_bag_problem();
}
Examples
Source: 416 Split equal sum subset
Title:
Give a non empty array that contains only positive integers. Whether the array can be divided into two subsets so that the sum of the elements of the two subsets is equal.
Note: the elements in each array will not exceed 100, and the size of the array will not exceed 200
Example 1: input: [1, 5, 11, 5] output: true explanation: the array can be divided into [1, 5, 5] and [11] Example 2: input: [1, 2, 3, 5] output: false explanation: an array cannot be divided into two elements and equal subsets
Idea:
Divide the array into two equal sets: the size of each subset is sum/2 (the maximum knapsack capacity is sum/2)
Each element can only be taken once (01 backpack)
Backpack Capacity = subset sum, item value = element size, item weight = element size
1.j means that the backpack capacity is j, and the maximum sum of subsets of J is dp[j]
2.dp[j]=max(dp[j],dp[j-nums[i]]+nums[i])
3. Full initialization to 0
4. Sequence: positive outside and negative inside
class Solution {
public:
bool canPartition(vector<int>& nums) {
int sum = 0;
// I in dp[i] represents the sum in the backpack
// The title says: the elements in each array will not exceed 100, and the size of the array will not exceed 200
// The total will not be more than 20000, and only half of them are required for the backpack, so the size of 10001 is OK
vector<int> dp(10001, 0);
for (int i = 0; i < nums.size(); i++) {
sum += nums[i];
}
if (sum % 2 == 1) return false;
int target = sum / 2;
// Start 01 Backpack
for(int i = 0; i < nums.size(); i++) {
for(int j = target; j >= nums[i]; j--) { // Each element must be non repeatable, so traverse from large to small
dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
}
}
// The elements in the collection can be summed exactly to target
if (dp[target] == target) return true;
return false;
}
};
Source: leetcode 1049
Title:
A pile of stones. The weight of each stone is a positive integer.
In each round, choose any two stones and smash them together. Suppose the weight of the stone is x and y, respectively, and x < = y. Then the possible results of crushing are as follows:
If x == y, both stones will be completely crushed; If {X= y. Then the stone weighing , x , will be completely crushed, and the stone weighing , y , will have a new weight of , y-x. In the end, there will be only one stone left at most. Returns the smallest possible weight of this stone. If there are no stones left, return 0.
Example: input: [2,7,4,1,8,1] output: 1 explanation: combine 2 and 4 to get 2, so the array is transformed into [2,7,1,8,1], combine 7 and 8 to get 1, so the array is transformed into [2,1,1,1], combine 2 and 1 to get 1, so the array is transformed into [1,1,1], combine 1 and 1 to get 0, so the number group is transformed into [1], which is the optimal value.
Idea:
Divide the stones into two groups as much as possible so that their sum is equal
1.j stands for a backpack with a capacity of j, which can hold up to dp[j] weight stones
2.dp[j]=max(dp[j],dp[j-stone[j]]+stone[j])
3. Initialize dp[0]=0, and others are also initialized to 0
4. External positive and internal negative
class Solution {
public:
int lastStoneWeightII(vector<int>& stones) {
vector<int> dp(15001, 0);
int sum = 0;
for (int i = 0; i < stones.size(); i++) sum += stones[i];
int target = sum / 2;
for (int i = 0; i < stones.size(); i++) { // Traverse items
for (int j = target; j >= stones[i]; j--) { // Traversal knapsack
dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);
}
}
return sum - dp[target] - dp[target];
}
};
reference resources: