How to understand "heap"

Heap sorting is an in-situ sorting algorithm with time complexity of O(nlogn)

There are two characteristics of the heap:

1. A complete binary tree
2. Each node in the heap must be greater than or equal to (or less than or equal to) the value of its left and right child nodes;

The heap whose value of each node is greater than or equal to the value of each node in the subtree is called "large top heap". The heap whose value of each node is less than or equal to the value of each node in the subtree is called "small top heap".

How to implement a "heap"

How to store a heap

Complete binary tree is more suitable for storing with array. Using arrays to store complete binary trees is very space efficient. Because there is no need to store the pointers of the left and right child nodes, the left and right child nodes and parent nodes of a node can be found simply through the subscript of the array.

What operations does the heap support

Insert an element into the heap

When inserting elements to the end, you need to perform heap operation: there are actually two kinds of heap, from bottom to top and from top to bottom. Here I'll first talk about the bottom-up heap method - follow the path of the node, up or down, compare, and then exchange

public class Heap {
  private int[] a; // Array, storing data from subscript 1
  private int n;  // The maximum number of data that the heap can store
  private int count; // Number of data stored in the heap

  public Heap(int capacity) {
    a = new int[capacity + 1];
    n = capacity;
    count = 0;
  }

  public void insert(int data) {
    if (count >= n) return; // Piled up
    ++count;
    a[count] = data;
    int i = count;
    while (i/2 > 0 && a[i] > a[i/2]) { // Bottom up stacking
      swap(a, i, i/2); // swap() function: exchange two elements with subscripts i and i/2
      i = i/2;
    }
  }
 }

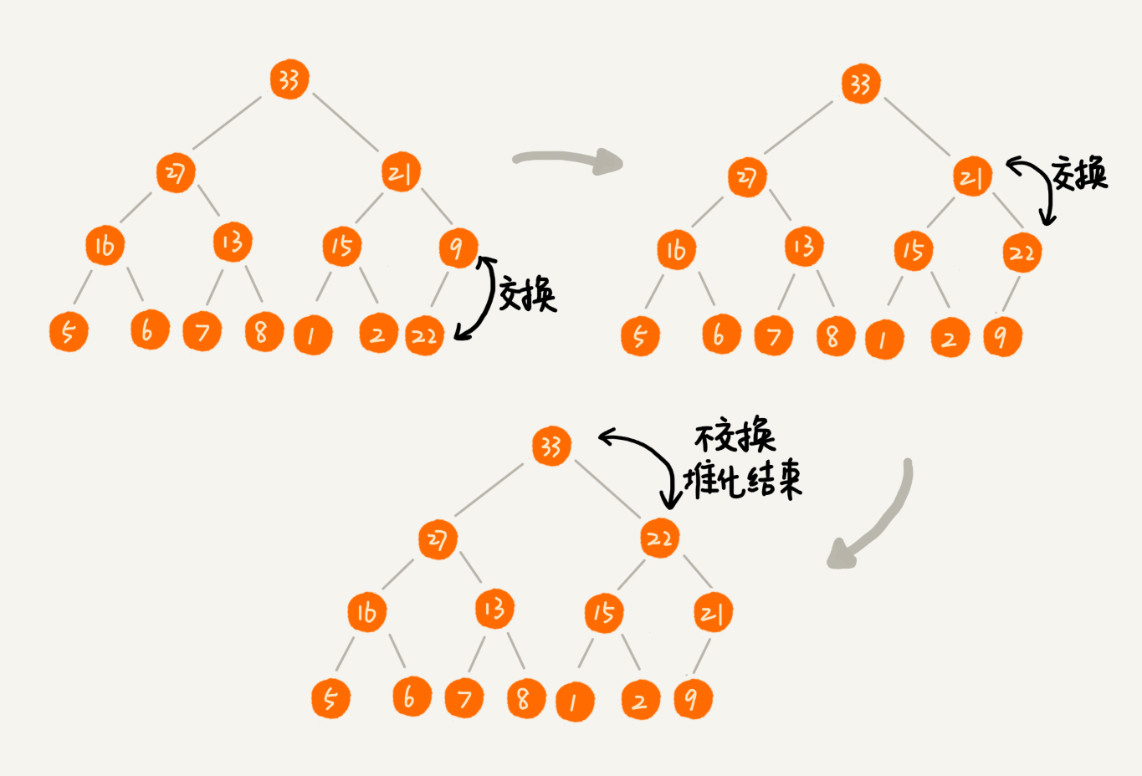
Delete heap top element

Idea 1: after deleting the heap top element, you need to put the second largest element on the heap top, and the second largest element will certainly appear in the left and right child nodes. Then we iteratively delete the second largest node, and so on, until the leaf node is deleted. This empty array method will appear

Idea 2: put the last node on the top of the heap, and then use the same parent-child node comparison method. For those that do not meet the size relationship between parent and child nodes, exchange two nodes, and repeat this process until the size relationship between parent and child nodes is met. This is the top-down stacking method.

Implementation code:

public void removeMax() {
  if (count == 0) return -1; // There is no data in the heap
  a[1] = a[count];
  --count;
  heapify(a, count, 1);
}

private void heapify(int[] a, int n, int i) { // Stacking from top to bottom
  while (true) {
    int maxPos = i;
    if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2;
    if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1;
    if (maxPos == i) break;
    swap(a, i, maxPos);
    i = maxPos;
  }
}

How to sort based on heap?

The time complexity of this sorting method is very stable, which is O(nlogn), and it is also an in-situ sorting algorithm. The process of heap sorting is divided into two steps:

1. Build pile

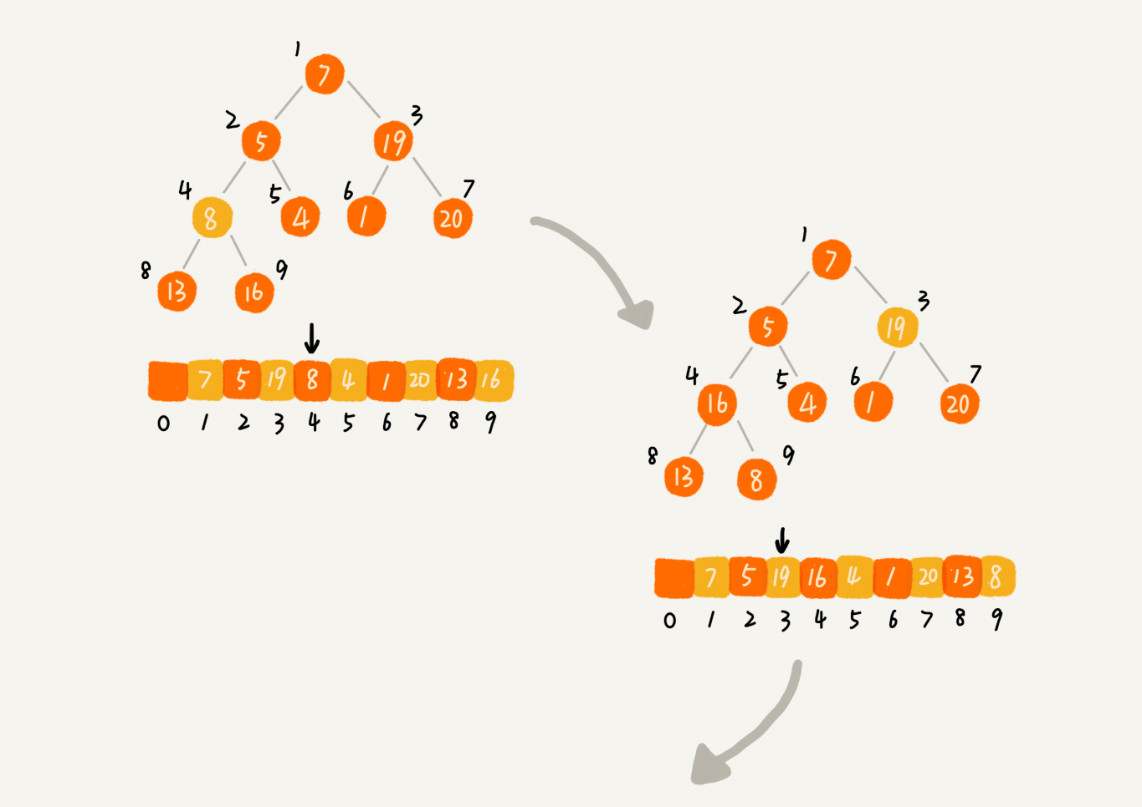
Idea 1: the array contains n data, but we can assume that at first, the heap contains only one data, that is, the data with subscript 1. Then, we call the previous insert operation to insert the data with subscripts from 2 to n into the heap in turn. In this way, we will organize the array containing N data into a heap. This method processes array data from front to back, and each data is stacked from bottom to top when it is inserted into the heap. Not recommended

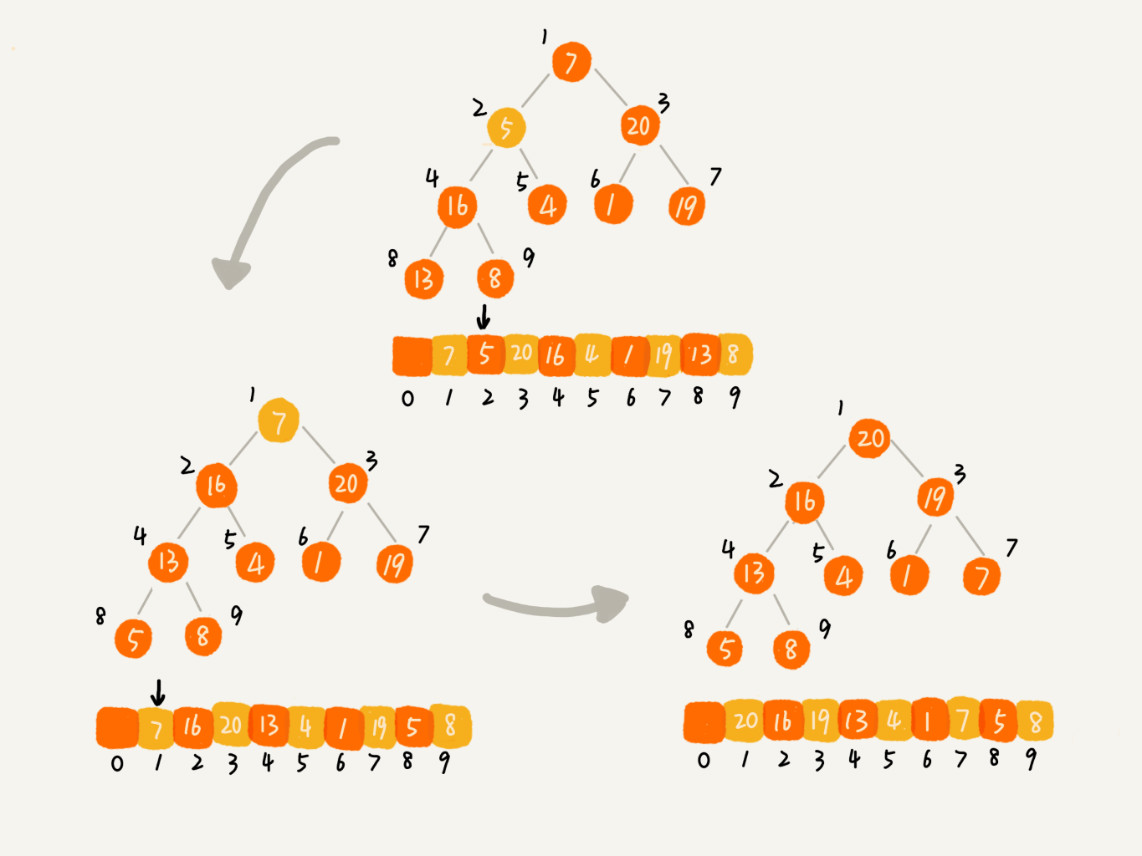
Idea 2: process the array from back to front, and each data is stacked from top to bottom. The following illustration:

Code implementation

private static void buildHeap(int[] a, int n) {
  for (int i = n/2; i >= 1; --i) {
    heapify(a, n, i);
  }
}

private static void heapify(int[] a, int n, int i) {
  while (true) {
    int maxPos = i;
    if (i*2 <= n && a[i] < a[i*2]) maxPos = i*2;
    if (i*2+1 <= n && a[maxPos] < a[i*2+1]) maxPos = i*2+1;
    if (maxPos == i) break;
    swap(a, i, maxPos);
    i = maxPos;
  }
}

Heap the data with subscripts from 2n to 1. The nodes with subscripts from 2n + 1 to n are leaf nodes. We don't need to heap. In fact, for a complete binary tree, the nodes with subscripts from 2n + 1 to n are leaf nodes.

The time complexity of heap building is O(n).

2. Sort

• After heap building, the data in the array is organized according to the characteristics of the large top heap. The first element in the array is the top of the heap, which is the largest element. We swap it with the last element, and the largest element is placed in the position with the subscript n.
• This process is a bit similar to the operation of "deleting the top element" mentioned above. After the top element is removed, we put the element with subscript n on the top of the heap, and then rebuild the remaining N − 1 elements into the heap through heap method. After the heap is completed, we take the elements at the top of the heap, put them in the position with subscript n − 1, and repeat the process until there is only one element marked 1 left in the heap, and the sorting is completed.

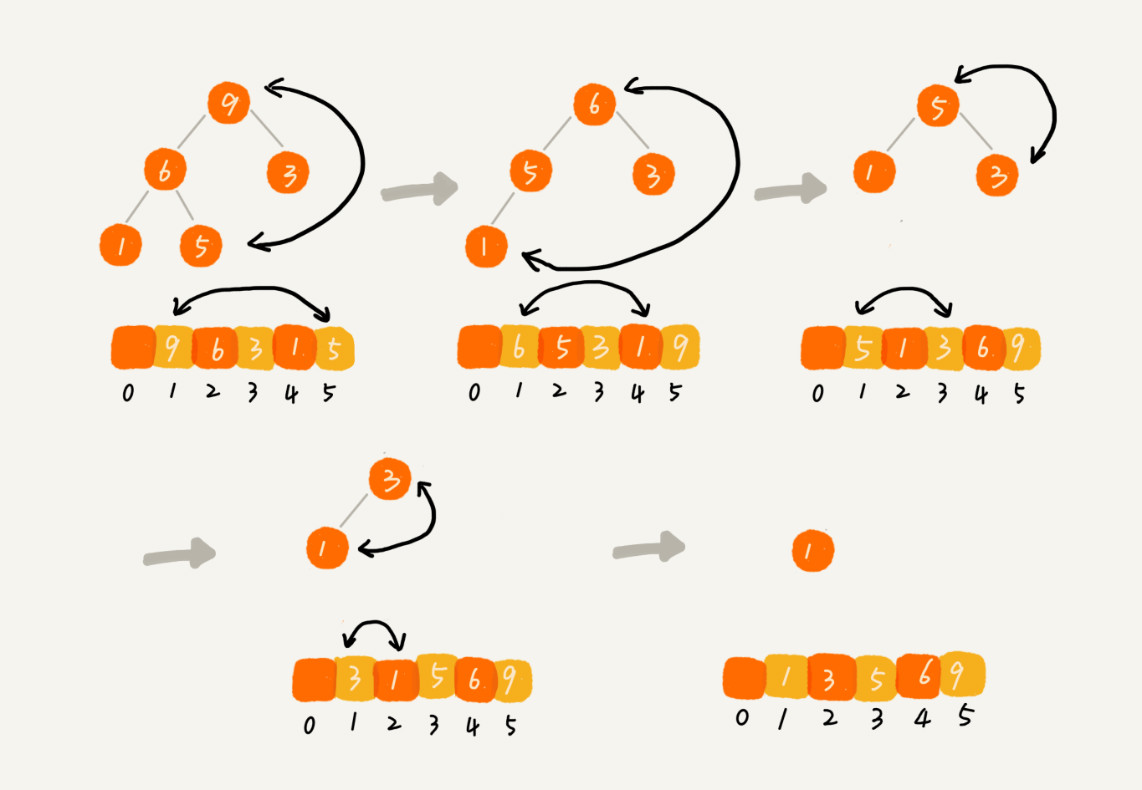
Heap sort procedure code:

// N represents the number of data, and the position of data in array a from subscript 1 to n.
public static void sort(int[] a, int n) {
  buildHeap(a, n);
  int k = n;
  while (k > 1) {
    swap(a, 1, k);
    --k;
    heapify(a, k, 1);
  }
}

Analyze the time complexity, space complexity and stability of heap sorting

1. The whole heap sorting process only needs a few temporary storage space, so heap sorting is an in-situ sorting algorithm.

2. Heap sorting includes two operations: heap building and sorting. The time complexity of heap building process is O(n), and the time complexity of sorting process is O(nlogn). Therefore, the overall time complexity of heap sorting is O(nlogn).

3. Heap sorting is not a stable sorting algorithm, because in the sorting process, there is the operation of exchanging the last node of the heap with the top node of the heap, so it is possible to change the original relative order of data with the same value.

Explanation: in the previous explanation and code, i assume that the data in the heap is stored from the position where the array subscript is 1. If the storage starts from 0, there is no change in the processing idea. The only change may be that the formula for calculating the subscripts of child nodes and parent nodes changes when the code is implemented. If the subscript of the node is i, the subscript of the left child node is 2 * i+1, the subscript of the right child node is 2 * i+2, and the subscript of the parent node is 2i − 1.

Answer title

First, heap sort data access is not as friendly as quick sort. For quick sort, data is accessed sequentially. For heap sorting, data is accessed by jumping. In heap sorting, the most important operation is data heap. For example, in the following example, the heap top node will access the elements with array subscripts 1, 2, 4 and 8 in turn, rather than local sequential access like quick sort. Therefore, this is not friendly to CPU cache.

Second, for the same data, in the sorting process, the data exchange times of heap sorting algorithm are more than that of quick sorting