I. The Concept of Algorithms

Algorithms: Algorithms are descriptions of steps to solve specific problems. They represent a finite sequence of instructions in a computer, and each instruction represents one or more operations.

2. The Characteristics of the Algorithms

1. Input and Output
The algorithm has zero or more inputs; the algorithm has at least one or more outputs.
2. Finiteness
It means that the algorithm automatically ends without infinite loops after performing a limited number of steps, and each step is completed within an acceptable time.
3. Certainty
Every step of the algorithm has a definite meaning, and no ambiguity occurs.
4. Feasibility
Each step of the algorithm must be feasible, that is to say, each step can be completed by a limited number of executions.

3. Requirements for Algorithmic Design

1. Correctness
The correctness of the algorithm means that the algorithm should have no ambiguity in input, output and processing, can correctly reflect the needs of the problem, and can get the correct answer to the problem.

2. Readability
Another purpose of algorithm design is to facilitate reading, understanding and communication.
3. Robustness
When the input data is not valid, the algorithm can also make relevant processing, rather than producing abnormal or strange results.
4. High Time Efficiency and Low Storage

IV. Efficiency Measurement of Algorithms

1. Efficiency Content of Execution Time Response Algorithms
   The execution time of the algorithm program can reflect the efficiency of the algorithm, that is, the advantages and disadvantages of the algorithm.
2. Is time absolutely credible?
   The operation of the program can not be separated from the computer environment (including hardware and operating system). It is not necessarily objective and accurate to compare the advantages and disadvantages of the algorithm only by running time.
   3. Time complexity and large "O" algorithm
   Time Complexity: Assuming that there is a function g, it takes time for algorithm A to process an example of a problem with a scale of n to be T(n)=O(g(n). Then O(g(n) is called the asymptotic time complexity of algorithm A, referred to as time complexity, which is denoted as T(n).
   Assuming that the time for each basic operation of the algorithm is a fixed unit of time, how many basic operations represent how many units of time will be spent.

"Big O notation": The constant factors in the scale function of the number of basic operations of measurement algorithms can be neglected.

Optimal Time Complexity, Worst Time Complexity, Average Time Complexity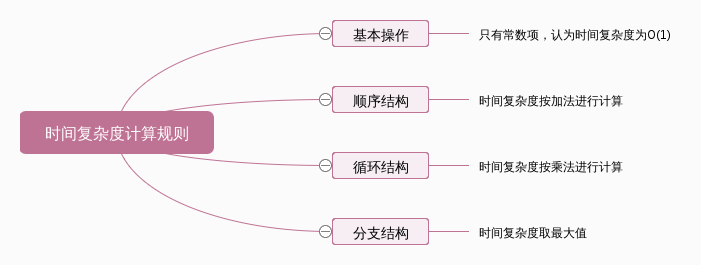

Without special explanation, the time complexity of the algorithms we analyze refers to the worst time complexity.

5. Time complexity

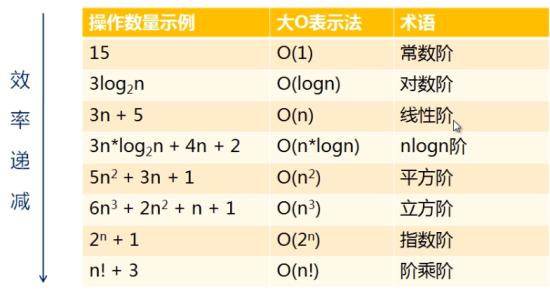
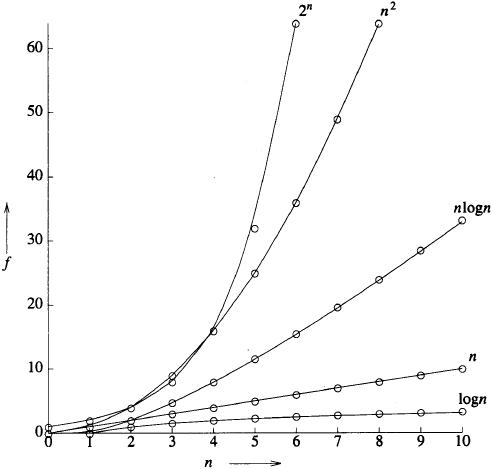
The timeiit module can be used to test the execution speed of a small piece of Python code

VI. Performance Analysis

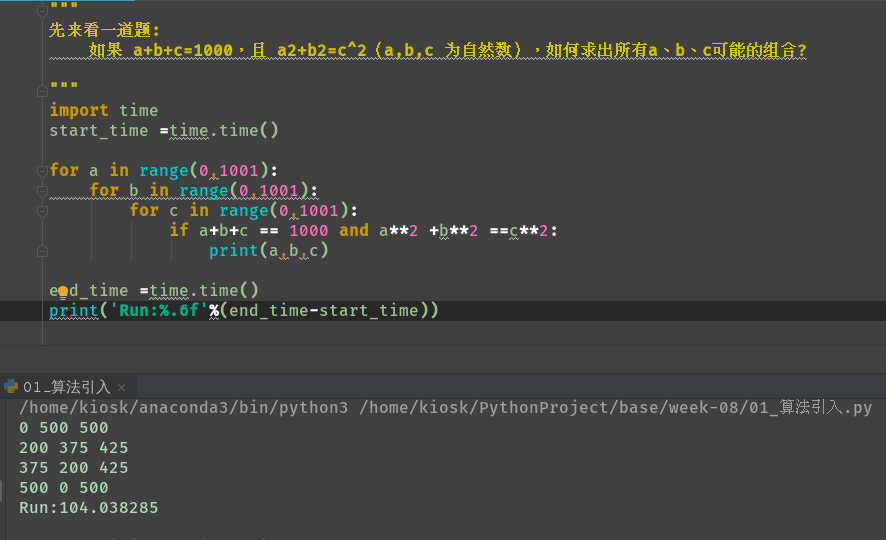
1. Let's start with a question:
If a+b+c=1000 and a2+b2=c^2 (a,b,c are natural numbers), how can we find all possible combinations of a, B and c?
Solution 1:

import time
start_time =time.time()

for a in range(0,1001):
    for b in range(0,1001):
        for c in range(0,1001):
            if a+b+c == 1000 and a**2 +b**2 ==c**2:
                print(a,b,c)

end_time =time.time()
print('Run:%6.f'%(end_time-start_time))  #Calculate program run time

Solution 2:

import time
start_time =time.time()

for a in range(0,1001):
    for b in range(0,1001-a):
        c = 1000-a-b
        if a**2 + b**2 == c**2:
            print(a, b, c)

end_time =time.time()
print('Run:%.6f'%(end_time-start_time))

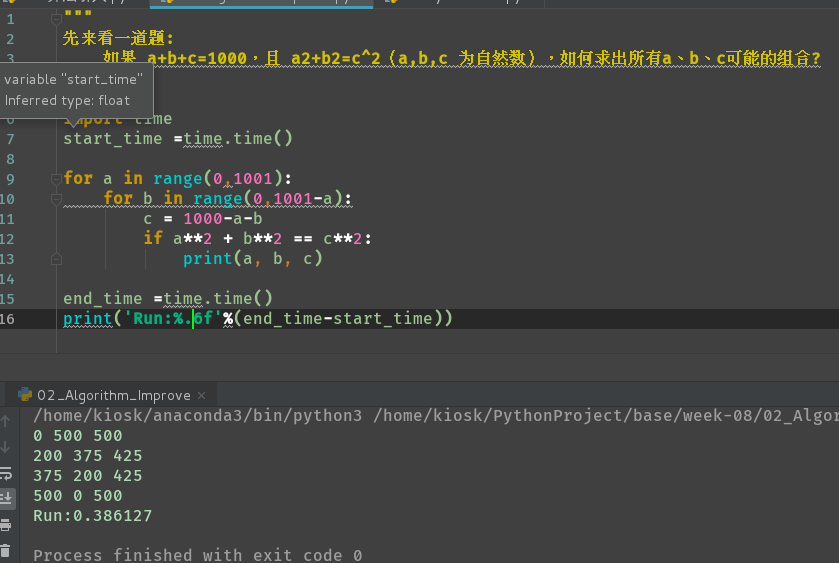
Compared with the two programs, although they can solve the problem, the running time of the two programs can reflect the importance of the algorithm.

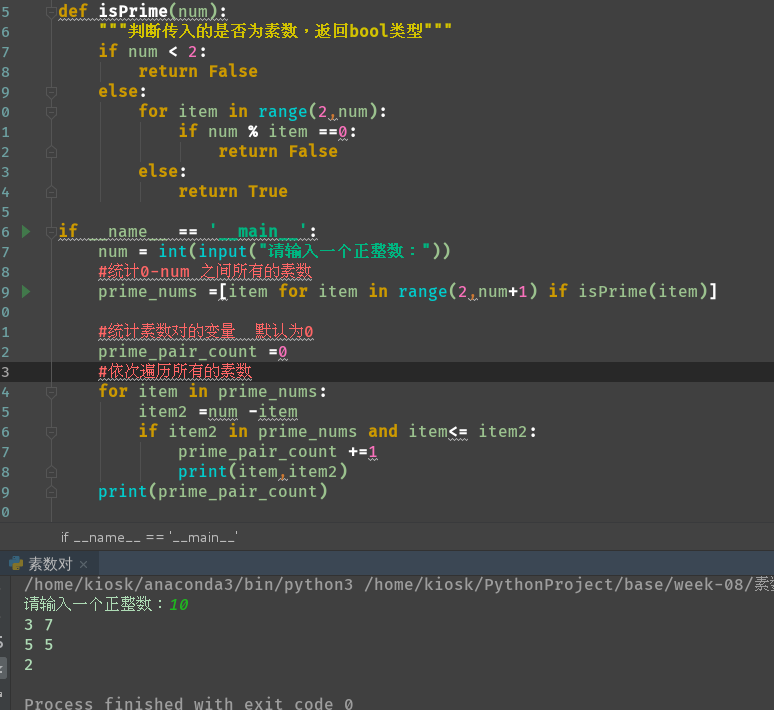
2. Find prime pairs - Given a positive integer, write a program to calculate how many pairs of prime sum equal to the input of the positive integer, and output the results. The input value is less than 1000.
For example, if the input is 10, the program should output a result of 2. (The sum of two pairs of prime numbers is 10, which is (5,5), (3,7).)

def isPrime(num):
    """Determine whether the incoming prime number is returned bool type"""
    if num < 2:
        return False
    else:
        for item in range(2,num):
            if num % item ==0:
                return False
        else:
            return True

if __name__ == '__main__':
    num = int(input("Please enter a positive integer:"))
    #Statistics of all prime numbers between 0-num
    prime_nums =[item for item in range(2,num+1) if isPrime(item)]

    #Statistical prime pair variables default to 0
    prime_pair_count =0
    #Traverse all prime numbers in turn
    for item in prime_nums:
        item2 =num -item
        if item2 in prime_nums and item<= item2:
            prime_pair_count +=1
            print(item,item2)
    print(prime_pair_count)

3. Test by generating lists

def list_JionOperator():
    """Create by connection operator"""
    li =[]
    for i in range(1000):
        li = li + [i]

def list_Append():
    """adopt append Method"""
    li =[]
    for i in range(1000):
        li.append(i)
def list_Generator():
    """Generating Formula by List"""
    li =[i for i in range(1000)]
def list_Range():
    list(range(1000))

if __name__ == '__main__':
    import timeit
    t1 =timeit.Timer('list_JionOperator()',"from __main__ import list_JionOperator")
    print(t1.timeit(number=1000))
    t2 = timeit.Timer('list_Append()', "from __main__ import list_Append")
    print(t2.timeit(number=1000))
    t3 =timeit.Timer('list_Generator()',"from __main__ import list_Generator")
    print(t3.timeit(number=1000))
    t4 = timeit.Timer('list_Range()', "from __main__ import list_Range")
    print(t4.timeit(number=1000))