▲ in graph theory, there are two ways of traversing trees: breadth first traversal and depth first traversal
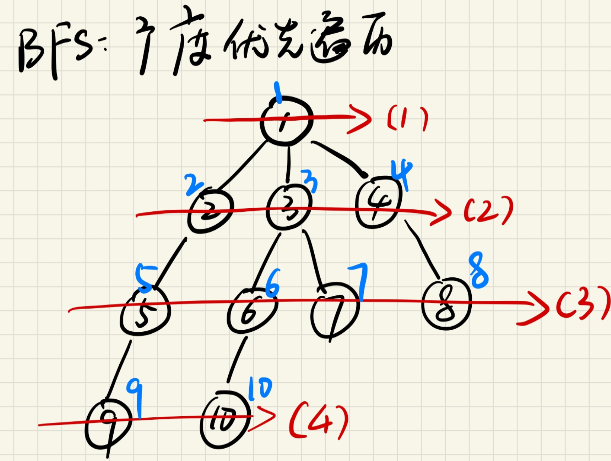
Breadth first traversal (BFS): starting from an un traversed node of the graph, traverse the adjacent nodes of the node first, and then traverse the adjacent nodes of each adjacent node in turn (i.e. traversal layer by layer)
For example:
Depth first traversal (DFS): start from an unreachable vertex V in the graph and go all the way to the end, then go back from the node at the end of the road to the previous node, and then go all the way from the other road. Repeat this process until all the points are traversed
For example:
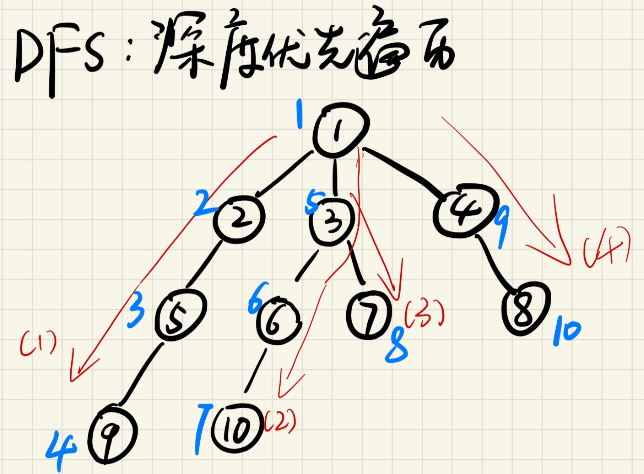
Starting from root node 1, its adjacent nodes are 2, 3 and 4 First traverse node 2, and then traverse nodes 5 and 9 downward (process (1)) The current node 9 has no child nodes At this time, it will go back from node 9 to the previous node 5 to judge whether node 5 has nodes other than 9. It does not continue to go back to 2, 2 and 5. It goes back to 1, 1 and node 3 other than 2. Therefore, it starts the depth first traversal from node 3 (start the (2) process) And so on until the end of traversal
Non recursive method is usually used for DFS: with the help of stack structure, the root node is stacked, the right node of its child node is stacked, and then the left node of its root node is stacked
For example, traverse the depth of the following binary tree first
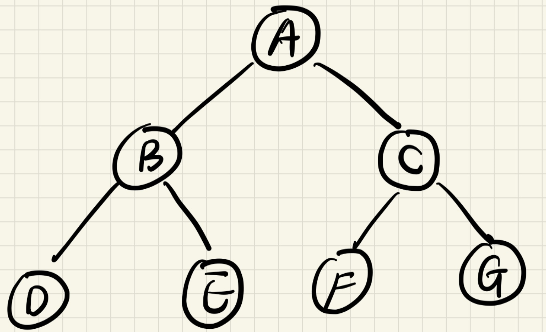
Root node a stacks, a stacks, C and B stacks, B stacks, e and D stacks, D stacks, e stacks, C stacks, G and f stacks, f stacks, G stacks. (A B D E C F G)
| Serial number | Stack | result |
|---|---|---|
| 1 | A | |
| 2 | A | |
| 3 | C B | A |
| 4 | A B | |
| 5 | C E D | A B |
| 6 | C | A B D E |
| 7 | A B D E C | |
| 8 | G F | A B D E C |
| 9 | A B D E C F G |
▲ state space tree: describes the tree structure of solution space
Each node in the tree is called a problem state
The path from the root to a state in the tree represents a tuple as a candidate solution, which is called the solution state of the state
The path from the root to a solution state is called the answer state as the tuple of the feasible solution
▲ the solution method of nodes in the state space tree generated by depth first pruning function is called backtracking method. Generally speaking, the backtracking method is to "go back" to the previous step and reselect when "feeling" that the original choice is not good or can not reach the goal
The method of generating nodes with breadth first and using pruning function is called branch and bound method
★ n queen question: n × N queens are placed on the n chessboard so that any two of them are not in the same row and the same slash
Analysis: since each queen should not be in the same row, for the sake of generality, it is assumed that the i-th queen is placed in row I (0 ≤ I < n), and queen[i] is the number of columns in which the i-th queen is located It is easy to know that the implicit constraints are ∀ i,j ∈ [0,n),i ≠ J (different rows), queen[i] ≠ queen[j] (different columns), | i-j ≠ queen[i]-queen[j] | (different slashes)
#include <iostream>
#include <cmath>
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
using namespace std;
const int maxn=16;//Upper limit (can be changed)
int queen[maxn],sum=0;
//Defines the number of feasible solutions of the global variable sum table. queen[i] number of feasible columns of the table
void display(int* queen,int n){
for(int i=0;i<n;i++){
cout<<"("<<i<<" "<<queen[i]<<")";
}
cout<<endl;
sum++;
}
bool check(int cur){
for(int i=0;i<cur;i++){//Start from line 0 and go down, so there is no need for constraints in different lines
if(queen[i]==queen[cur]||abs(i-cur)==abs(queen[i]-queen[cur]))//Constraints: different slashes for different columns
return false;
}
return true;
}
void dfs(int cur,int n){//cur is the current number of traversal layers (rows)
if(n<=0||n>maxn){//Illegal or cross-border situations
return;
}
if(cur==n){//Traverse to the last layer for direct output
display(queen,n);
}
else{
for(int i=0;i<n;i++){
queen[cur]=i;
if(check(cur))//If the constraint conditions are met, continue to traverse the next layer
dfs(cur+1,n);
}
}
}
int main(int argc, char** argv) {
int n;
cin>>n;
dfs(0,n);
cout<<"The total of "<<n<<" Queen's solutions:"<<sum;
return 0;
}
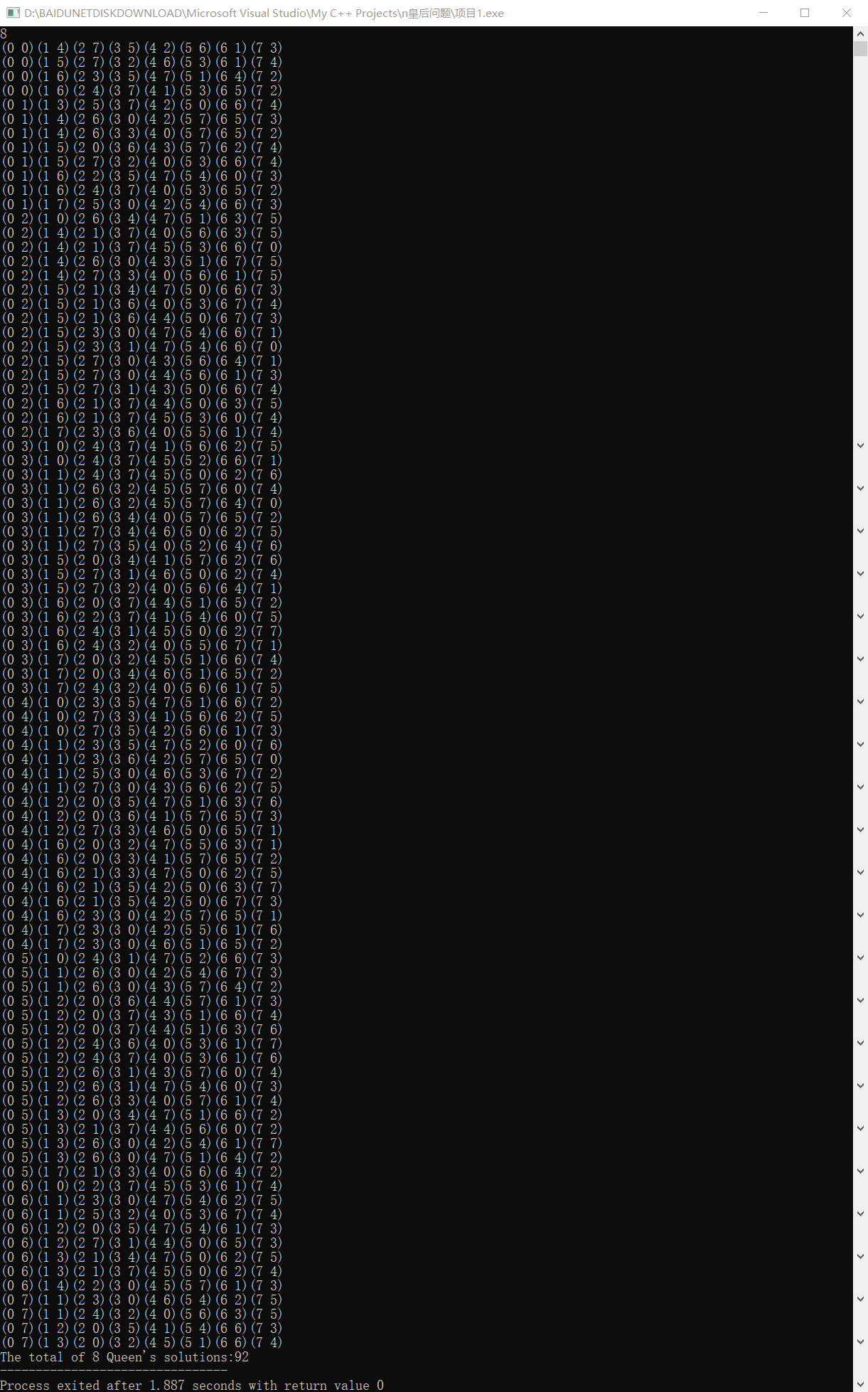
When n=8, the result is:
Supplement: algorithm design and analysis Chen Huinan version n queen problem code:
#include <iostream>
#include <cmath>
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
using namespace std;
#define N 4 // 4. Problem code (changeable)
int x[N];
bool Place(int k,int i,int* x){//Determine whether two queens are in the same column or on the same slash
for(int j=0;j<k;j++){
if((x[j]==i)||(abs(x[j]-i)==abs(j-k)))//Constraints: different slashes for different columns
return false;
}
return true;
}
void NQueens(int k,int* x){//Recursive function for solving n-queen problem
for(int i=0;i<N;i++){//Try the number of all optional columns
if(Place(k,i,x)){//Satisfy constraints
x[k]=i;
if(k==N-1){//Last row successfully output column
for(int j=0;j<N;j++)
cout<<x[j]<<" ";
cout<<endl;
}
else//Continue to traverse downward without traversing to the last line
NQueens(k+1,x);
}
}
}
int main(int argc, char** argv) {
NQueens(0,x);
return 0;
}