The main reason for the tree is that there are too many application questions. (the algorithm problem has only been tested twice, which is very simple. It is a traversal; the algorithm problem is in the next article)

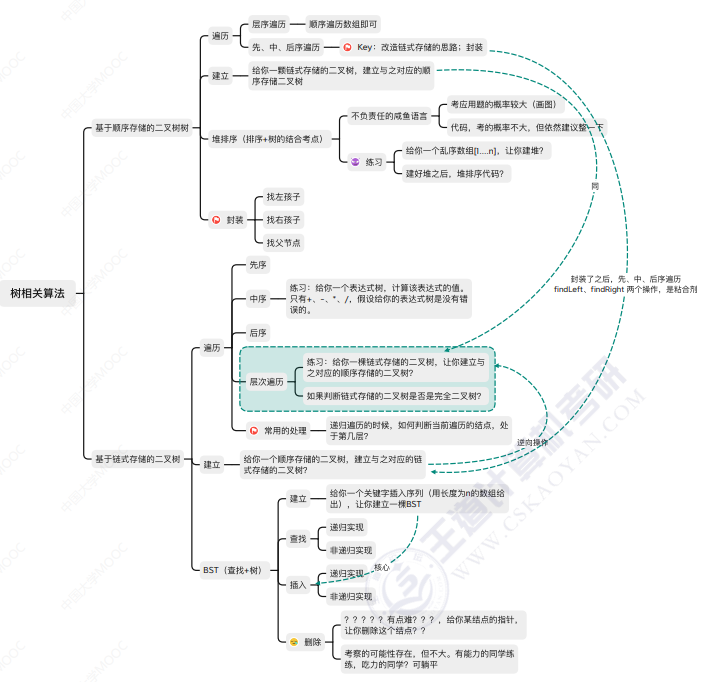
Mind map

Basic concepts

Develop habits: distinguish between degrees and sum of degrees:

Number of nodes = total degree + 1

Degree: refers to the maximum degree of each node in a tree

Chain type

If the chained storage is a multi tree, it can only be the child's representation.
Therefore, the big question can only be the piece of binary tree.

ergodic

Recursive traversal is simple.

void preOrder(Node *p)
{
	if(p!=NULL)
	{
		visit(p);
		preOrder(p->lchild);
		preOrder(p->rchild);
	}
}
// Pre order, middle order and subsequent traversal are not difficult

⭐ Non recursive traversal.

The middle order and the front order are basically the same, both of which are 1 ️⃣ Enter the left node of the stack all the way to the left. At the end of the stack, when you find that the left child at a certain point is empty, you can't enter the stack again; two ️⃣ Pop up the top of the stack, access: 2 ️⃣. one ️⃣ If there is a left child, perform 1 ️⃣； two ️⃣. two ️⃣ If there is no right child, perform 2 ️⃣.

void inOrder(BTNode *root)
{
	Stack <BTNode>;
	InitStack(S);
	BTNode p = root;
	while(p || isEmpty(S))
	{
		if(p)
		{
			push(S,p);
			p = p -> lchild;
		}
		else{
			pop(S,p);
			visit(p); // Middle order traversal, first - > root - > right
			p = p -> rchild;
		}
	}
}

void preOrder(BTNode *root)
{
	Stack <BTNode>;
	InitStack(S);
	BTNode p = root;
	while(p || isEmpty(S))
	{
		if(p)
		{
			visit(p); // First order traversal, root - > first - > right
			push(S,p);
			p = p -> lchild;
		}
		else{
			pop(S,p);
			p = p -> rchild;
		}
	}
}

Post order traversal requires a flag processing on the root of a subtree. Because the latter order is left and right roots. After a certain subtree of a certain root completes the search, it will not know which subtree exits the stack. Therefore, additional processing is required.

void postOrder(BTNode *root)
{
	Stack <BTNode>;
	InitStack(S);
	BTNode p = root;
	while(p || isEmpty(S))
	{
		if(p)
		{
			push(S,p);
			p = p -> lchild;
		}
		else{
			getTop(S,p);
			if(p-> rchild && p->rchild != r)
				p = p -> rchild;
			else{
					pop(S,p)
					visit(p);
					r = p;
					p = NULL;
	
			}
		}
	}
}

⭐ Several points to be explained:

1. In post order traversal, after traversing a point, the elements in the stack are the ancestors of the point
2. In the non recursive traversal duration of post order traversal, there will be no stack empty at a certain time except the end time. When the stack is empty and only ends, the root node returns to the stack.

structure

👍🏼 Given a middle order sequence and a preorder sequence, construct the tree?

Tree preInCreate(int A[], int B[], int l1, int l2, int h1, int h2)
{// A(l1, h1) sequence; Order in B(l2, h2)
	
	Node *root =  (Node*)malloc(sizeof(Node));
	root->data = A[l1];
	// Cycle, Division
	for(i = l2; B[i]!= root->data; i++);
	llen = i - l2;
	rlen = h2 - i;
	
	// Recursive establishment of left subtree
	if(llen) // If there is a left subtree
		root->lchild = preInCreate(A,B,l1+1, l1+llen, l2, l2+llen-1);
	else root->lchild = NULL;
	
	// Recursive establishment of right subtree
	if(rlen) // If there is a right subtree
		root->rchild = preInCreate(A,B,h1-rlen+1, h1, i+1, h2);
	else root->lchild = NULL;
	
	return root;
}

Clue binary tree

Essence: traversal.

Use the empty finger to point to the precursor or successor.

structure

Algorithm program:

There are pre and P. Recursive left subtree first; Then check whether the left pointer of P is empty. If it is empty, attach; See whether the right subtree of pre is empty. If it is empty, connect to p; Then recursive right subtree.

If the order is first and then adjusted. [it's impossible to test something deeper!]

Node *pre;
void Inthread(Node *p) //Middle order
{
	Inthread(p->lchild);

	if(!p->lchild)// No left child, connect
	{
		p -> lchild = pre;
		p -> ltag = 1;
	}
	if(! pre -> rchild){
		pre -> rchild = p;
		pre -> rtag = 1;
	}
	pre = p; 
	Inthread(p->rchild);
}

ergodic

In fact, the clue binary tree can be traversed from two directions: from front to back and from back to front.

From front to back, we need to find successors.

The following storage locations of the current node p are nothing more than two:

1. Rtag = current node's rtag = 1. At this p oint, (right child = = right clue) is the successor.
2. Rtag of current node p = = 0. At this time, in the subtree with the right child as the root, we need to find the first node traversed in the middle order. (in fact, it is the bottom left corner of the right subtree.)

Encapsulate it into two functions:

Node *find_next(Node *p)
{
	if (p->rtag == 1)
		return p -> rchild;
	else
		return find_first_node(p->rchild);
}
Node *find_first_node(Node p)
{
	while(p->ltag == 0) p = p -> lchild;
	return p;
}

So we can get the traversal from front to back:

void Inorder_thread(Node *T)
{
	for(Node *p = find_first_node(T); p!=NULL; p = find_next(p))
		visit(p);
}

Manually convert clues

In fact, it is to write a sequence, then draw a diagram and connect it manually. The key is to know that the direction of the arrow always points to the next.

Moreover, the clue that can point to NULL must be the first or last.

Pit father of post order clue tree

The traversal of the post order clue tree may be broken, while the middle order and pre order will not.

For example:

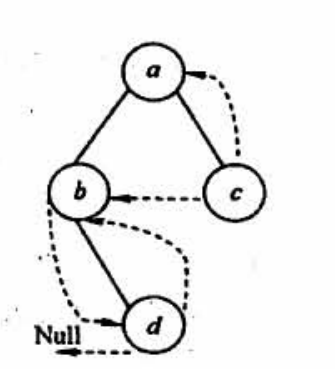
Such a post order clue tree, D → b → c → a. But the clue of b → c is nothing. (because the right child is connected to the successor node, and a child has been connected d).