Reference resources: https://blog.csdn.net/zhouyuheng2003/article/details/80163139#comments
Title:
Let m be a positive integer and a be an integer. If the order of a module M equals phi (m), then a is called a primitive root of a module M. (where_(m) denotes the Euler function of m)
Give a prime number P and find the primitive root of the minimum P.
Input
Enter a prime number P(3 <= P <= 10 ^ 9)
Output
The original root with the smallest output P.
Input example
3
Output example
2
Relevant knowledge:
Let's first understand the meaning of the order of a module m: the n-th-power module M remainder 1 of a, in which the order of a module M is the order that satisfies the minimum condition.
If n==phi(m), then a is a primitive root of M.
And:
(The inverse element of Euler's theorem is universal)
Euler's Theorem: For any two positive integers a, m (m >=2) has
Namely:
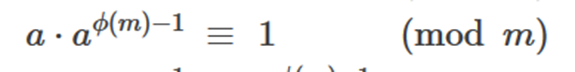
Therefore:
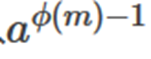It is the inverse element of a under module m. _
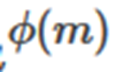The number of positive integers less than m and mutually prime with M
For m, the minimum primitive root a is obtained.
a -> 2...
if a^phi(m)!=1MOd m
continue;
i -> 1..(phi(m)-1)
If a^i==1 mod m
Explain that this a does not conform
If they all agree, then this a is the answer.Code: (This violence will be timed out)
// #include <bits/stdc++.h>
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
#define ll long long
int phi(int n)
{
int m=sqrt(n+0.5);
int ans=n;
for(int i=2;i<=m;i++) if(n%i==0)
{
ans=ans/i*(i-1);
while(n%i==0) n/=i;
}
if(n>1)
{
ans=ans/n*(n-1);
}
return ans;
}
ll pow(ll a,ll b,ll mod)
{
ll base=a;
ll sum=1;
while(b)
{
if(b&1)
sum=(sum*base)%mod;
b>>=1;
base=(base*base)%mod;
}
return sum;
}
int G(int n)
{
int Phi=phi(n);
int g;
for(g=2;;g++)
{
if(pow(g,Phi,n)!=1) continue;
int flag=0;
for(int i=1;i<Phi;i++)
{
if(pow(g,i,n)==1)
{
flag=1;
break;
}
}
if(!flag) break;
}
return g;
}
int main()
{
int p;
while(~scanf("%d",&p))
{
int g=G(p);
printf("%d\n",g);
}
return 0;
}A little improvement:
It's the factor that changes i from 1 to phi(m)-1 to phi(m) in ergodic g^i
// #include <bits/stdc++.h>
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
#define ll long long
int phi(int n)
{
int m=sqrt(n+0.5);
int ans=n;
for(int i=2;i<=m;i++) if(n%i==0)
{
ans=ans/i*(i-1);
while(n%i==0) n/=i;
}
if(n>1)
{
ans=ans/n*(n-1);
}
return ans;
}
ll pow(ll a,ll b,ll mod)
{
ll base=a;
ll sum=1;
while(b)
{
if(b&1)
sum=(sum*base)%mod;
b>>=1;
base=(base*base)%mod;
}
return sum;
}
int q[100100];
int G(int n)
{
int Phi=phi(n);
int g;
int cnt=0;
int temp=(int)(sqrt(Phi+0.5));
for(int i=1;i<=temp;i++)
{
if(Phi%i==0)
{
q[cnt++]=i;
if(i!=1)q[cnt++]=Phi/i;
}
}
for(g=2;;g++)
{
if(pow(g,Phi,n)!=1) continue;
int flag=0;
for(int i=0;i<cnt;i++)
{
if(pow(g,q[i],n)==1)
{
flag=1;
break;
}
}
if(!flag) break;
}
return g;
}
int main()
{
int p;
while(~scanf("%d",&p))
{
int g=G(p);
printf("%d\n",g);
}
return 0;
}Implementation code: --"The code is really hard to understand. (Fortunately, now you can see the following.)
The following code only changes the factor of i-traversal phi(m) traversing g^i to the factor of phi(m) traversal only in the section [sqrt (phi(m)~phi (m)-1].
i don't know why i changed range i to [1, sqrt (phi(m)]. The factor of phi(m) is WA.
/* 51nod 1135 Primitive root */
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstring>
using namespace std;
#define ll long long
#define INF 0x3f3f3f3f
const int mod=1e9+7;
ll prime[100];
int cnt=0;
void make_prime(ll x)
{
for(int i=2;i*i<=x;i++) if(x%i==0)
{
prime[cnt++]=i;
while(x%i==0) x/=i;
}
if(x>1)
prime[cnt++]=x;
}
ll quick_mod(ll base, int n, int mod) //Fast power remainder
{
ll ans=1;
while(n)
{
if(n&1) ans=ans*base%mod;
base=base*base%mod;
n>>=1;
}
if(ans<0)
ans+=mod;
return ans;
}
int main()
{
int m;
scanf("%lld", &m);
make_prime(m-1);
for(int i=2;i<m;i++)
{
int flag=1;
for(int j=0;j<cnt;j++)
{
int x=(m-1)/prime[j];
if(quick_mod(i,x,m)==1)
{
flag=0;
break;
}
}
if(flag)
{
printf("%d\n",i);
break;
}
}
return 0;
}