2609 Slendest Spanning Tree

1. 1.0 seconds
2.  
3. 131,072.0 KB
4.  
5. 20 points
6.  
7. Level 3

The thinness of a tree is defined as the difference between the maximum edge weight and the minimum edge weight of the tree.

Now there is an undirected graph with n points and m edges to find out the thinness of the spanning tree with the smallest thinness.

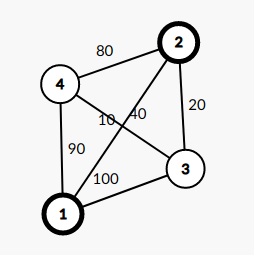
In the data shown in the figure, the three edges of the spanning tree selected by the optimal selection scheme are (1-4, 4-2, 1-3), so the answer is 100-80=20.

Put it away

input

Line 1: Two positive integers n,m, n denote the number of points in the graph, and M denotes the number of edges in the graph. (2<=n<=100,0<=m<=(n*(n_1)/2))
Line 2 - Line m+1: Each row has three positive integers, u,v,w, indicating that there is an edge with a weight of w between u and V. (1<=u, v<=n, 1<=w<=10000)

output

Output an integer to represent the slimness of the spanning tree with the smallest slimness.

sample input

4 6
1 2 10
1 3 100
1 4 90
2 3 20
2 4 80
3 4 40

sample output

20

Enumerate maximum and minimum values.

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn=20000+66;
const ll mod=1e9+7;
int N,M;
struct node
{
    int u;
    int v;
    int w;
} a[maxn];
bool cmp(const node&a,const node&b)
{
    return a.w<b.w;
}
int minn=9999999;
int f[maxn];
int finds(int x)
{
    return x==f[x]?x:f[x]=finds(f[x]);
}
void unions(int x,int y)
{
    int fx=finds(x);
    int fy=finds(y);
    if(fx!=fy)
    {
        f[fx]=fy;
    }
}
int work()
{
    for(int i=1; i<=N; i++)
        f[i]=i;
    int flag=0;
    for(int i=1; i<=M; i++)
    {
        int l=a[i].w;
        int r=l;
        int num=1;
        for(int k=1; k<=N; k++)
        f[k]=k;
        unions(a[i].u,a[i].v);
        for(int j=i+1; j<=M; j++)
        {
            if(finds(a[j].u)!=finds(a[j].v))
            {
                num++;
                unions(a[j].u,a[j].v);
                r=max(r,a[j].w);
            }
        }
        if(num==N-1)
        {
            flag=1;
            minn=min(minn,r-l);
        }
    }
    return minn;
}
int main()
{
    scanf("%d%d",&N,&M);

    for(int i=1; i<=M; i++)
    {
        scanf("%d %d %d",&a[i].u,&a[i].v,&a[i].w);
    }
    sort(a+1,a+M+1,cmp);
    int ans1=work();
    printf("%d\n",ans1);//467  506
}
/*#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int maxn=20000+66;
const ll mod=1e9+7;
int N,M;
struct node
{
    int u;
    int v;
    int w;
} a[maxn];
bool cmp(const node&a,const node&b)
{
    return a.w<b.w;
}
int minn=9999999;
int f[maxn];
int finds(int x)
{
    return x==f[x]?x:f[x]=finds(f[x]);
}
void unions(int x,int y)
{
    int fx=finds(x);
    int fy=finds(y);
    if(fx!=fy)
    {
        f[fx]=fy;
    }
}
int work(int i1,int j1)
{
    for(int i=1; i<=N; i++)
        f[i]=i;
    int num=2;
    node x1=a[i1];
    node x2=a[j1];
    unions(x1.u,x1.v);
    unions(x2.u,x2.v);
    if(abs(x1.w-x2.w)>minn)return minn;
    for(int i=i1; i<=j1; i++)
    {
        // if(a[i].w<x1.w||a[i].w>x2.w)continue;
        if(num==N-1)
            break;
        if(finds(a[i].u)!=finds(a[i].v))
        {
            num++;
            unions(a[i].u,a[i].v);
        }
    }
    if(num==N-1)
    {
        minn=abs(x1.w-x2.w);
        return abs(x1.w-x2.w);
    }
    return 9999999;
}
int main()
{
    scanf("%d%d",&N,&M);

    for(int i=1; i<=M; i++)
    {
        scanf("%d %d %d",&a[i].u,&a[i].v,&a[i].w);
    }
    sort(a+1,a+M+1,cmp);
    for(int i=1; i<=M; i++)
        for(int j=i+1; j<=M; j++)
                minn=min(minn,work(i,j));
    printf("%d\n",minn);//467  506
}*/