51Nod1383 -- power of integer to 2

It's easy to think that for a certain number i, its combination can be regarded as each combination of i-1 plus a 1, but this 1 may merge with other 1 to generate a new combination;

When i is an odd number, it is found that one of them has not been merged all the time; for each combination of i-1, insert a 1. If a merger occurs, it will only occupy the position of 1 that needs to be merged and new combination will be generated, so no new combination will be generated at last;

But when i is an even number, because every combination of i-1 must have a 1 that has never been merged. At this time, inserting a 1 will merge and generate a new combination. At this time, find all the combinations of i-1 that have a 1 left. The combination of two ones must generate a new combination, and there will be no 1 in the new combination. How can these new combinations be recursive? After dividing these combinations by two, we find that these are the combinations of i/2.

Finally, the recurrence formula is established

 

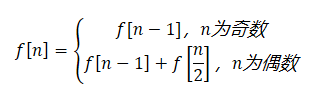
For ease of understanding, a certain number of combinations can be listed.

1=1

2=1+1=2

3=1+1+1=1+2

4=1+1+1+1=1+1+2=2+2=4

5=1+1+1+1+1=1+1+1+2=1+2+2=1+4

6=1+1+1+1+1+1=1+1+1+1+2=1+1+2+2=2+2+2=2+4=1+1+4

#include <bits/stdc++.h>
#define For(i,x,y) for(int i=(x);i<=(y);++i)
#define Fov(i,x,y) for(int i=(x);i>=(y);--i)
#define Fo(i,x,y) for(int i=(x);i<(y);++i)
#define midf(a,b) ((a)+(b)>>1)
#define L(_) (_)<<1
#define R(_) ((_)<<1)|1
#define fi first
#define se second
#define ss(_) scanf("%s",_)
#define si(_) scanf("%d",&_)
#define sii(x,y) scanf("%d%d",&x,&y)
#define siii(x,y,z) scanf("%d%d%d",&x,&y,&z)
#define sl(_) scanf("%I64d",&_)
#define mem(x,y) memset(x,y,sizeof(x))
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int>P;
inline int read()
{
    char ch=getchar(); int x=0, f=1;
    while(ch<'0'||ch>'9') { if(ch=='-') f=-1; ch=getchar();}
    while('0'<=ch&&ch<='9') { x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}
const int inf=0x3f3f3f3f;
const double pi=acos(-1.0);
const int mod=1e9+7;
const int n_max=1e6+10;
int a[n_max];

int main()
{
	//freopen("in.txt","r",stdin);
	int n; si(n);
	a[0]=1;
	For(i,1,n)
	{
	    if(i&1) a[i]=a[i-1];
	    else a[i]=(a[i-1]+a[i>>1])%mod;
	}
	printf("%d\n",a[n]);
    return 0;
}