An explanation of binary tree from Baidu Encyclopedia:
In computer science, a binary tree is a tree structure with at most two subtrees per node. Usually, subtrees are called "left subtree" and "right subtree". Binary trees are often used to implement binary search trees and binary heaps.
A binary tree with a depth of K and 2^k-1 nodes is called a full binary tree. The characteristic of this tree is that the number of nodes on each layer is the maximum number of nodes. In a binary tree, except for the last layer, if the other layers are full, and the last layer is either full, or there are several consecutive nodes on the right, then the binary tree is a complete binary tree. The depth of a complete binary tree with n nodes is floor(log2n)+1. A complete binary tree with a depth of K has at least 2k-1 leaf nodes and at most 2k-1 nodes.
The structure of binary tree:
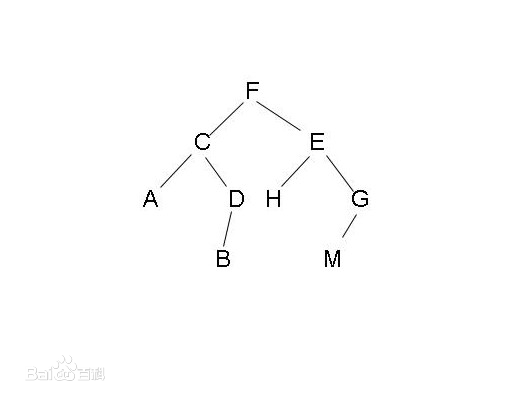
Declarations of binary tree nodes:
static final class Entry<T extends Comparable<T>>{
//Preserved data
private T item;
//Left tree
private Entry<T> left;
//Right subtree
private Entry<T> right;
//Parent node
private Entry<T> parent;
Entry(T item,Entry<T> parent){
this.item = item;
this.parent = parent;
}
}Class properties:
//root node
private Entry<T> root;
//Data volume
private int size = 0;Binary tree adds data:
/**
* Additive elements
* @param item Elements to be added
* @return Added elements
*/
public T put(T item){
//Each time data is added, it traverses downward from the root node
Entry<T> t = root;
if (t == null){
//The current fork tree is empty, and the new node is set to the root node and the parent node is null.
root = new Entry<>(item,null);
size++;
return root.item;
}
//Natural sorting results, if the incoming data is less than the current node returns - 1, greater than the current node returns 1, otherwise returns 0
int ret = 0;
//Record parent node
Entry<T> p = t;
while (t != null){
//Comparing with the current node
ret = item.compareTo(t.item);
p = t;
//The insertion node is smaller than the current node. Set the current node to the left sub-node, and then compare it with the left sub-node to find the appropriate location by analogy.
if (ret < 0)
t = t.left;
//Greater than the current node
else if (ret > 0)
t = t.right;
else {
//Cover up old values when they are equal
t.item = item;
return t.item;
}
}
//Create a new node
Entry<T> e = new Entry<>(item,p);
//Put the new node in the right place according to the comparison result
if (ret < 0)
p.left = e;
else
p.right = e;
size++;
return e.item;
}In the process of put ting, Comparable < T > compareTo is used to compare the size of two elements, so the elements stored in the binary tree must inherit the Comparable < T > class and override the compareTo method.
Binary Tree Delete Data
/**
* Delete elements
* If the deletion element is subdivided, it can be divided into four parts: no child node, only left node, only right node, and two child nodes.
* 1)It's easy to do without child nodes, just delete them directly.
* 2)Only the left node or the right node, the two cases are handled in the same way, but in the opposite direction, so together,
* The left node (right node) of the parent node of the deleted node is pointed to the child node of the deleted node, and the left node (right node) is pointed to the parent node of the deleted node.
* 3)There are two sub-nodes, which is relatively complex:
* Find the precursor or or successor node of the deleted node, assign the value of the precursor or successor node to the deleted node, and then delete the precursor or successor node. The essence is to delete precursor or or successor nodes
* The characteristics of the precursor node:
* 1)If the deleted left child node has no right child node, then the left child node is the precursor node.
* 2)If the left child of the deleted node has the right child, the last node on the right is the precursor node.
* The characteristics of successor nodes are as follows:
* Contrary to the precursor node, it is always the right child node, or the left-most child node of the right child node; for example, if the deletion node is c, the precursor node is m, and the successor node is n.
* a
* / \
* b c
* / \ / \
* d e f g
* / \ / \ / \ / \
* @param item Delete element h I J K L M n o
* @return Delete result
*/
public boolean remove(T item){
//Get the deleted node
Entry<T> delEntry = getEntry(item);
if (delEntry == null) return false;
//Delete the parent node of the node
Entry<T> p = delEntry.parent;
size--;
//Case 1: No child nodes
if (delEntry.left == null && delEntry.right == null){
//Delete node as root node
if (delEntry == root){
root = null;
}else {//Non root node
//The left node of the parent node is deleted
if (delEntry == p.left){
p.left = null;
}else {//Delete the right node
p.right = null;
}
}
//Case 2: Only the left node is deleted
}else if (delEntry.right == null){
Entry<T> lc = delEntry.left;
//The deleted node is the root node, and the left node of the deleted node is set to the root node.
if (p == null) {
lc.parent = null;
root = lc;
} else {//Non root node
if (delEntry == p.left){//Delete the left node
p.left = lc;
}else {//Delete the right node
p.right = lc;
}
lc.parent = p;
}
//Case 3: Only the right node is deleted
}else if (delEntry.left == null){
Entry<T> rc = delEntry.right;
//Delete the root node
if (p == null) {
rc.parent = null;
root = rc;
}else {//Delete non-root nodes
if (delEntry == p.left)
p.left = rc;
else
p.right = rc;
rc.parent = p;
}
//Scenario 4: Delete a node with two child nodes
}else {//There are two nodes, find the successor node, assign the value to the deletion node, and then delete the successor node.
Entry<T> successor = successor(delEntry);//Get successor nodes
delEntry.item = successor.item;
//The successor node is the right child node
if (delEntry.right == successor){
//Right child node has right child node
if (successor.right != null) {
delEntry.right = successor.right;
successor.right.parent = delEntry;
}else {//Right child node has no child node
delEntry.right = null;
}
}else {//Successor node must be left node
successor.parent.left = null;
}
return true;
}
//Let gc recycle
delEntry.parent = null;
delEntry.left = null;
delEntry.right = null;
return true;
}
/**
* Getting Node Nodes
* @param item Get node
* @return The acquired node, possibly null
*/
private Entry<T> getEntry(T item){
Entry<T> t = root;
int ret;
//Traverse from the root node
for (;t != null;){
ret = item.compareTo(t.item);
if (ret < 0)
t = t.left;
else if (ret > 0)
t = t.right;
else
return t;
}
return null;
}
/**
* Finding successor nodes
* @param delEntry Delete node
* @return Successor node
*/
private Entry<T> successor(Entry<T> delEntry) {
Entry<T> r = delEntry.right;//r node must not be empty
while (r.left != null){
r = r.left;
}
return r;
}Binary tree acquisition node
/**
* Determine whether the element exists
* @param item Search element
* @return Result
*/
public boolean contains(T item){
return getEntry(item) != null;
}
/**
* Getting Node Nodes
* @param item Get node
* @return The acquired node, possibly null
*/
private Entry<T> getEntry(T item){
Entry<T> t = root;
int ret;
//Traverse from the root node
for (;t != null;){
ret = item.compareTo(t.item);
if (ret < 0)
t = t.left;
else if (ret > 0)
t = t.right;
else
return t;
}
return null;
}Because my example is to store an element, and the element obtained is consistent with the element passed in, so I use contains method to judge that returning true means that the acquisition is successful, not returning the result obtained. Of course, if you change the elements stored in entry to kv, you can use the get method.
Traversal of Binary Trees
The traversal of binary tree can be divided into three kinds: pre-order traversal, middle-order traversal and follow-up traversal. The middle-order traversal is the most commonly used traversal method, because it traverses the ascending order of the results.
Preorder traversal:
/**
* Preorder traversal
* @param e Start traversing elements
*/
public void prevIterator(Entry<T> e){
if (e != null) {
System.out.print(e.item + " ");
prevIterator(e.left);
prevIterator(e.right);
}
}Intermediate traversal:
/**
* Sequential traversal
* @param e
*/
public void midIterator(Entry<T> e){
if (e != null){
midIterator(e.left);
System.out.print(e.item + " ");
midIterator(e.right);
}
}Post-order traversal:
/**
* Subsequent traversal
* @param e Start traversing elements
*/
public void subIterator(Entry<T> e){
if (e != null) {
subIterator(e.left);
subIterator(e.right);
System.out.print(e.item + " ");
}
}package com.rainple.collections;
/**
* Two fork tree
* @param <T>
*/
public class BinaryTree<T extends Comparable<T>> {
//root node
private Entry<T> root;
//Data volume
private int size = 0;
public BinaryTree(){}
/**
* Additive elements
* @param item Elements to be added
* @return Added elements
*/
public T put(T item){
//Each time data is added, it traverses downward from the root node
Entry<T> t = root;
size++;
if (t == null){
//The current fork tree is empty, and the new node is set to the root node and the parent node is null.
root = new Entry<>(item,null);
return root.item;
}
//Natural sorting results, if the incoming data is less than the current node returns - 1, greater than the current node returns 1, otherwise returns 0
int ret = 0;
//Record parent node
Entry<T> p = t;
while (t != null){
//Comparing with the current node
ret = item.compareTo(t.item);
p = t;
//The insertion node is smaller than the current node. Set the current node to the left sub-node, and then compare it with the left sub-node to find the appropriate location by analogy.
if (ret < 0)
t = t.left;
//Greater than the current node
else if (ret > 0)
t = t.right;
else {
//Cover up old values when they are equal
t.item = item;
return t.item;
}
}
//Create a new node
Entry<T> e = new Entry<>(item,p);
//Put the new node in the right place according to the comparison result
if (ret < 0)
p.left = e;
else
p.right = e;
return e.item;
}
public void print(){
midIterator(root);
}
/**
* Sequential traversal
* @param e
*/
public void midIterator(Entry<T> e){
if (e != null){
midIterator(e.left);
System.out.print(e.item + " ");
midIterator(e.right);
}
}
/**
* Get the root node
* @return root node
*/
public Entry<T> getRoot(){return root;}
/**
* Preorder traversal
* @param e Start traversing elements
*/
public void prevIterator(Entry<T> e){
if (e != null) {
System.out.print(e.item + " ");
prevIterator(e.left);
prevIterator(e.right);
}
}
/**
* Subsequent traversal
* @param e Start traversing elements
*/
public void subIterator(Entry<T> e){
if (e != null) {
subIterator(e.left);
subIterator(e.right);
System.out.print(e.item + " ");
}
}
/**
* Getting Node Nodes
* @param item Get node
* @return The acquired node, possibly null
*/
private Entry<T> getEntry(T item){
Entry<T> t = root;
int ret;
//Traverse from the root node
for (;t != null;){
ret = item.compareTo(t.item);
if (ret < 0)
t = t.left;
else if (ret > 0)
t = t.right;
else
return t;
}
return null;
}
/**
* Determine whether the element exists
* @param item Search element
* @return Result
*/
public boolean contains(T item){
return getEntry(item) != null;
}
/**
* Delete elements
* If the deletion element is subdivided, it can be divided into four parts: no child node, only left node, only right node, and two child nodes.
* 1)It's easy to do without child nodes, just delete them directly.
* 2)Only the left node or the right node, the two cases are handled in the same way, but in the opposite direction, so together,
* The left node (right node) of the parent node of the deleted node is pointed to the child node of the deleted node, and the left node (right node) is pointed to the parent node of the deleted node.
* 3)There are two sub-nodes, which is relatively complex:
* Find the precursor or or successor node of the deleted node, assign the value of the precursor or successor node to the deleted node, and then delete the precursor or successor node. The essence is to delete precursor or or successor nodes
* The characteristics of the precursor node:
* 1)If the deleted left child node has no right child node, then the left child node is the precursor node.
* 2)If the left child of the deleted node has the right child, the last node on the right is the precursor node.
* The characteristics of successor nodes are as follows:
* Contrary to the precursor node, it is always the right child node, or the left-most child node of the right child node; for example, if the deletion node is c, the precursor node is m, and the successor node is n.
* a
* / \
* b c
* / \ / \
* d e f g
* / \ / \ / \ / \
* @param item Delete element h I J K L M n o
* @return Delete result
*/
public boolean remove(T item){
//Get the deleted node
Entry<T> delEntry = getEntry(item);
if (delEntry == null) return false;
//Delete the parent node of the node
Entry<T> p = delEntry.parent;
size--;
//Case 1: No child nodes
if (delEntry.left == null && delEntry.right == null){
//Delete node as root node
if (delEntry == root){
root = null;
}else {//Non root node
//The left node of the parent node is deleted
if (delEntry == p.left){
p.left = null;
}else {//Delete the right node
p.right = null;
}
}
//Case 2: Only the left node is deleted
}else if (delEntry.right == null){
Entry<T> lc = delEntry.left;
//The deleted node is the root node, and the left node of the deleted node is set to the root node.
if (p == null) {
lc.parent = null;
root = lc;
} else {//Non root node
if (delEntry == p.left){//Delete the left node
p.left = lc;
}else {//Delete the right node
p.right = lc;
}
lc.parent = p;
}
//Case 3: Only the right node is deleted
}else if (delEntry.left == null){
Entry<T> rc = delEntry.right;
//Delete the root node
if (p == null) {
rc.parent = null;
root = rc;
}else {//Delete non-root nodes
if (delEntry == p.left)
p.left = rc;
else
p.right = rc;
rc.parent = p;
}
//Scenario 4: Delete a node with two child nodes
}else {//There are two nodes, find the successor node, assign the value to the deletion node, and then delete the successor node.
Entry<T> successor = successor(delEntry);//Get successor nodes
delEntry.item = successor.item;
//The successor node is the right child node
if (delEntry.right == successor){
//Right child node has right child node
if (successor.right != null) {
delEntry.right = successor.right;
successor.right.parent = delEntry;
}else {//Right child node has no child node
delEntry.right = null;
}
}else {//Successor node must be left node
successor.parent.left = null;
}
return true;
}
//Let gc recycle
delEntry.parent = null;
delEntry.left = null;
delEntry.right = null;
return true;
}
/**
* Finding successor nodes
* @param delEntry Delete node
* @return Successor node
*/
private Entry<T> successor(Entry<T> delEntry) {
Entry<T> r = delEntry.right;//r node must not be empty
while (r.left != null){
r = r.left;
}
return r;
}
public int size(){return size;}
public boolean isEmpty(){return size == 0;}
public void clear(){
clear(getRoot());
root = null;
}
private void clear(Entry<T> e){
if (e != null){
clear(e.left);
e.left = null;
clear(e.right);
e.right = null;
}
}
static final class Entry<T extends Comparable<T>>{
//Preserved data
private T item;
//Left tree
private Entry<T> left;
//Right subtree
private Entry<T> right;
//Parent node
private Entry<T> parent;
Entry(T item,Entry<T> parent){
this.item = item;
this.parent = parent;
}
}
}Test code example:
public static void main(String[] args) {
BinaryTree<Integer> binaryTree = new BinaryTree<>();
//Release data
binaryTree.put(73);
binaryTree.put(22);
binaryTree.put(532);
binaryTree.put(62);
binaryTree.put(72);
binaryTree.put(243);
binaryTree.put(42);
binaryTree.put(3);
binaryTree.put(12);
binaryTree.put(52);
System.out.println("size: " + binaryTree.size());
binaryTree.put(52);
System.out.println("After adding the same element size: " + binaryTree.size());
//Judging whether data exists
System.out.println("Does the data exist?" + binaryTree.contains(12));
//Sequential traversal
System.out.print("Intermediate order traversal results: ");
binaryTree.midIterator(binaryTree.getRoot());
System.out.println();
//Preorder traversal
System.out.print("Previous traversal results: ");
binaryTree.prevIterator(binaryTree.getRoot());
System.out.println();
//Post order traversal
System.out.print("Follow-up traversal results: ");
binaryTree.subIterator(binaryTree.getRoot());
//Delete data
System.out.println();
binaryTree.remove(62);
System.out.println("After deleting the data, determine whether it exists:" + binaryTree.contains(62));
//Empty Binary Tree
binaryTree.clear();
System.out.print("Intermediate traversal after clearing data: ");
binaryTree.midIterator(binaryTree.getRoot());
}Test results:
size: 10 After adding the same element, size:10 Does the data exist: Intermediate order traversal results: 3 12 22 42 52 62 72 73 243 532 Previous ergodic results: 73 22 3 12 62 42 52 72 532 243 Follow-up traversal results: 123 52 42 72 62 22 243 532 73 After deleting the data, determine whether it exists:false Intermediate traversal after clearing data:
Pure handwritten demo, welcome to correct any mistakes, thank you for reading!!!