Recursive Implementation of Half Search Algorithms (Binary Search)

Binary lookup recursive implementation code:

/**
 * Recursive implementation of binary search
 */
int bin_search(int key[], int low, int high, int x){
    
    int mid;
    
    if (low > high)
        return -1;
    else{
        mid = (low + high)/2;
        
        if (key[mid] == x) return mid;
        
        if (x > key[mid]) {
            low = mid + 1;
            return bin_search(key, low, high, x); // Find in the second half of the sequence
        }else{
            high = mid - 1;
            return bin_search(key, low, high, x); //Finding in the first half of the sequence
        }
    }
}

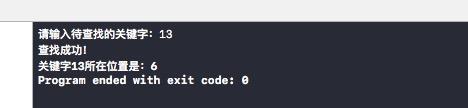
Test:

int main(int argc, const char * argv[]) {
  
    int str[11] = {1,1,2,3,5,8,13,21,34,55,89};
    int n, addr;
    
    printf("Please enter the keywords to be found:");
    scanf("%d", &n);
    
    addr = bin_search(str, 0, 10, n);
    
    if (addr != -1) {
        printf("Find success!\n Keyword%d The location is:%d\n", n, addr);
    }else{
        printf("Find failed!\n");
    }
    return 0;
}

Recursive Implementation of Half Search Algorithms

The Hanoi Tower Problem

Origin of the Hanoi Tower Problem

The Hanoi Pagoda (also known as the Hanoi Pagoda) problem is a puzzle toy originating from an ancient Indian legend. When Brahman created the world, he made three diamond pillars, on which 64 gold discs were stacked in order of size from bottom to top. Brahman was ordered to rearrange the disc from below on another post in order of size. It is also stipulated that the disc can not be enlarged on a small disc and that only one disc can be moved at a time between the three columns.

Hanoi Tower Problem is abstracted into Mathematical Problem

Assuming that three towers named X, Y and Z have n disks with different diameters and large numbers of 1,2,3 on the tower X, it is now required to move n disks on the X axis to Z and stack them in the same order. When the disks move, they must follow a sequence of rules:

• Only one disk can be moved at a time.
• The disc can be inserted into any tower base of X, Y and Z.

• At no time can a larger disc be pressed on a smaller one.

  
  
  
  

Consideration of Hanoi Tower with Recursive Thought

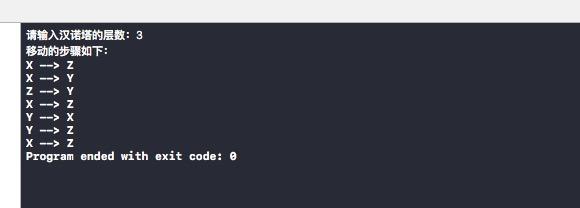
The steps to realize the Hanoi Tower Problem are as follows:

• First move the first n-1(63) plates to Y to ensure that the large plate is under the small plate;
• Then move the bottom n(64) plates to Z.
• Finally, n-1(63) plates on Y are moved to Z.

Then the problem will be resolved into two problems:

• Question 1: Move n-1(63) plates on X to Y with Z;
• Question 2: Move n-1(63) plates on Y to Z by X.

The idea of solving these two steps is the same:
Question 1:

• First move the first n-2(62) plates to Z to ensure that the large plate is under the small plate;
• Then move the bottom n-1(63) plates to Y.
• Finally, n-2(62) plates on Z are moved to Y.
  Question two:
• First move the first n-2(62) plates to X to ensure that the large plate is under the small plate;
• Then move the bottom n-1(63) plates to Z.
• Finally, n-2(62) plates on Z are moved to Y.

Get the same rule: this is actually a recursive problem.

Code:

void hanoi(int n, char x, char y, char z){
    
    if (n == 1)  // There's only one story.
        printf("%c --> %c\n", x, z);
    else{
        hanoi(n - 1, x, z, y);          // Move n-1 plate from x to y with z
        printf("%c --> %c\n", x, z);     // Move the n-th plate from x to z
        hanoi(n-1, y, x, z);            // Move n-1 plate from y to z with x
    }
}

Test code:

int main(int argc, const char * argv[]) {

    int n;
    printf("Please enter the number of floors of the Hanoi Tower:");
    scanf("%d", &n);
    printf("The moving steps are as follows:\n");
    
    hanoi(n, 'X', 'Y', 'Z');
    
    return 0;
}

Hanoi Tower Recursive Algorithms

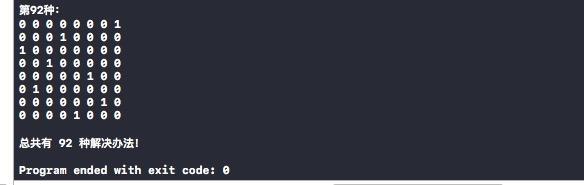
Recursive Solution to the Eight Queens Problem

The Eight Queens Problem is a chess-based problem: How can eight queens be placed on an 8*8 chessboard so that no one queen can eat the other queens directly? In order to achieve this goal, neither queen can be in the same horizontal, vertical or diagonal line.

The Code of Solving Eight Queens Problem by Recursion

#include <stdio.h>

int count = 0;

/**
 * Judge if there is danger
 */
int notdanger(int row,int j,int (*chess)[8]){
    
    int i,k;
    
    //Judging Column Direction
    for(i=0;i<8;i++){
        if(*(*(chess+i)+j)==1) return 0; //This list of queens already exists
    }
    
    //Judge the upper left
    for(i=row,k=j;i>=0&&k>=0;i--,k--){
        if(*(*(chess+i)+k)==1) return 0; //Queen already exists in the upper left
    }
    
    //Judge the lower right
    for(i=row,k=j;i<8&&k<8;i++,k++){
        if(*(*(chess+i)+k)==1) return 0; //Queen already exists on the lower right
    }
    
    //Judge the lower left
    for(i=row,k=j;i<8&&k>=0;i++,k--){
        if(*(*(chess+i)+k)==1) return 0; //Queen already exists on the lower left
    }
    
    //Judge the upper right
    for(i=row,k=j;i>=0&&k<8;i--,k++){
        if(*(*(chess+i)+k)==1) return 0; //Queen already exists in the upper right
    }
    
    return 1;
}

/**
 * Parametric row: Starting row
 * Parametric n: Number of columns
 * Parameter (* chess)[8]: Pointer to each line of the chessboard
 */
void eightqueen(int row,int n,int (*chess)[8]){
    
    int chess2[8][8],i,j;  // Temporary chessboard
    
    for(i=0;i<8;i++){
        for(j=0;j<8;j++){
            chess2[i][j] = chess[i][j]; // Temporary chessboard assignment to chessboard
        }
    }
    
    if(row == 8){
        printf("The first%d Species:\n",count + 1);
        
        for(i=0;i<8;i++){
            for(j=0;j<8;j++){
                printf("%d ",*(*(chess2+i)+j));
            }
            printf("\n");
        }
        
        count ++;
        
    }else {
        //Judging if this position is dangerous
        //If it's dangerous, keep going.
        for(j=0;j<n;j++){
            if(notdanger(row,j,chess)){ //Judging whether it is dangerous
                for(i=0;i<8;i++){ // No danger
                    *(*(chess2+row)+i)=0;
                }
                *(*(chess2+row)+j)=1;
                eightqueen(row+1,n,chess2);
            }
        }
    }
}

int main(int argc, const char * argv[]) {

    int chess[8][8];  // 8*8 chessboard
    int i,j;
    
    //Initialize the chessboard to 0
    for(i=0;i<8;i++){
        for(j=0;j<8;j++){
            chess[i][j]=0;
        }
    }
    eightqueen(0,8,chess);//Traverse by unit of conduct from line 0
    
    printf("\n All in all %d A solution!\n\n",count);
    return 0;
}