1. Dijkstra algorithm

Finding the shortest path from one vertex to all other vertices is an algorithm that generates the shortest path in increasing order of path length.

Algorithmic ideas:

Generate algorithms in increasing order of path length:
The vertex set V is divided into two groups:
(1) S: The set of vertices that have been calculated (initially containing only the source point V0)
(2) V-S=T: an undetermined set of vertices
Add the vertices of T to S in increasing order, guaranteeing:
(1) The length of each other vertex from source point V0 to S is not greater than the shortest path length of any vertex from V0 to T.
(2) Each vertex corresponds to a distance value
Vertex in S: Length from V0 to this vertex
Vertex in T: The shortest path length from V0 to this vertex that includes only the vertex in S as the intermediate vertex
Basis: can prove the weight of V0 to the vertex Vk in T, or the direct path from V0 to Vk, or the sum of the path weights from V0 to the vertex in S to Vk
(Evidence against evidence)
Shortest path steps
The algorithm steps are as follows:
1. Initial time S={V0},T={remaining vertices}, the distance value corresponding to the vertices in T
If <V0, Vi>, d(V0,Vi) is <V0, Vi>the weight on the arc
If <V0 does not exist, Vi>, d(V0,Vi) is 0
2. Select a vertex from T whose distance value is the smallest W and is not in S, and add S
3. Modify the distance values of the vertices in the remaining T: If W is added as the intermediate vertex and the distance value from V0 to Vi is shortened, modify the distance value
Repeat steps 2 and 3 until S contains all vertices, that is, W=Vi.

2. Floyd algorithm

Find the shortest path from all vertices to all vertices.

Algorithmic ideas:

1, start with any one-sided path.The distance between all two points is the weight of the edge, and if there is no edge connecting between the two points, the weight is infinite.
2. For each pair of vertices u and v, see if there is a vertex w that makes the path from u to w to V shorter than known.If it is updated.
Express the graph with the adjacency matrix G. If there is a path from Vi to Vj, G[i,j]=d, D represents the length of the path; otherwise, G[i,j]=infinity.Defines a matrix D to record the information of the inserted point, D[i,j] denotes the point that needs to pass from Vi to Vj, and initializes D[i,j]=j.Insert each vertex into the diagram and compare the distance after the interpolation point with the original distance, G[i,j] = min (G[i,j], G[i, k]+G[k, j]), if the value of G[i,j] becomes smaller, D[i,j]=k.G contains information about the shortest path between two points, while D contains information about the shortest path.
For example, look for a path from V5 to V1.According to D, if D(5,1)=3 means that V3 passes through V3 from V5 to V1. The path is {V5,V3,V1}. If D(5,3)=3, V5 is directly connected to V3. If D(3,1)=1, V3 is directly connected to V1.

Advantages and disadvantages:

Floyd algorithm is suitable for APSP(All Pairs Shortest Paths), which is a dynamic programming algorithm with the best dense map effect and positive or negative edge weights.This algorithm is simple and effective, because the triple loop structure is compact, it is more efficient than executing the |V| sub-Dijkstra algorithm for dense graphs.
Advantages: Easy to understand, can calculate the shortest distance between any two nodes, simple coding
Disadvantages: High time complexity makes it unsuitable for computing large amounts of data.

The algorithm code is as follows:

/* Graph.h header file */
/*Include graph creation: depth-first traversal of graph, width-first traversal of graph*/
/*Minimum spanning tree containing graph: Prim algorithm, Kruskal algorithm*/
/*Shortest path algorithm with graph: Dijkstra algorithm, Floyd algorithm*/
#include<iostream>
#include"LinkQueue.h"
#define MAXVEX 100
#define MAXEDGE 100
#define INFINITY 65535
#define TRUE 1
#define FALSE 0
typedef char VertexType;
typedef int EdgeType;
typedef int Boolean;
typedef int Patharc[MAXVEX];		/*Array for storing shortest path Subscripts*/
typedef int ShortPathTable[MAXVEX];		/*Weights and values for the shortest path stored at each point*/
typedef int Pathmatrix[MAXVEX][MAXVEX];
typedef int ShortPathTable_Floyd[MAXVEX][MAXVEX];

using namespace std;

/*Graph building using adjacency matrix*/
class MGraph{
public:
	VertexType vexs[MAXVEX];
	EdgeType arc[MAXVEX][MAXVEX];
	int numVertexes,numEdges;
};

/*Establishing adjacency matrix representation of undirected network graph*/
void CreateMGraph(MGraph *G)
{
	int i,j,k,w;
	cout<<"Enter the number of vertices and edges:"<<endl;
	cin>>G->numVertexes>>G->numEdges;
	cin.clear();
	cout<<"Enter vertex information:"<<endl;
	for(i=0;i<G->numVertexes;i++)
	{
		cin>>G->vexs[i];
		cin.clear();
	}
	for(i=0;i<G->numVertexes;i++)
		for(j=0;j<G->numVertexes;j++)
		{
			if (i==j)
				G->arc[i][j]=0;
			else
				G->arc[i][j]=INFINITY;
		}
	for(k=0;k<G->numEdges;k++)
	{
		cout<<"Input Edge ( vi,vj)Superscript i，subscript j And w:"<<endl;
		cin>>i>>j>>w;
		cin.clear();
		G->arc[i][j]=w;
		G->arc[j][i]=G->arc[i][j];
	}
}

/*Depth-first recursive algorithm for adjacency matrix*/
Boolean visited[MAXVEX];	/*Array of access flags*/
void DFS(MGraph G,int i)
{
	int j;
	visited[i]=TRUE;
	cout<<G.vexs[i];	/*Print vertices or other operations*/
	for(j=0;j<G.numVertexes;j++)
		if(G.arc[i][j]==1 && !visited[j])
			DFS(G,j);	/*Recursive calls to adjacent vertices for access*/
}
/*Depth-first traversal of adjacency matrices*/
void DFSTraverse(MGraph G)
{
	cout<<"\n The depth-first traversal results are:"<<endl;
	int i;
	for(i=0;i<G.numVertexes;i++)
		visited[i]=FALSE;	/*Initializing all vertex States is an unreached state*/
	for(i=0;i<G.numVertexes;i++)
		if(!visited[i])	/*Calling DFS on vertices that have not been visited will only execute once if the graph is connected*/
			DFS(G,i);
	cout<<endl;
}

/*A Width Traversal Algorithm for Adjacency Matrix*/
void BFSTraverse(MGraph G)
{
	cout<<"The breadth-first traversal results are:"<<endl;
	int i,j;
	LinkQueue Q;
	for(i=0;i<G.numVertexes;i++)
		visited[i]=FALSE;
	for(i=0;i<G.numVertexes;i++)
	{
		if(!visited[i])
		{
			visited[i]=TRUE;
			cout<<G.vexs[i];
			Q.EnQueue(i);
			while(!Q.QueueEmpty())
			{
				Q.DeQueue(&i);
				for(j=0;j<G.numVertexes;j++)
				{
					if(G.arc[i][j]==1 && !visited[j])
					{
						visited[j]=TRUE;
						cout<<G.vexs[j];
						Q.EnQueue(j);
					}
				}
			}
		}
	}
	cout<<endl;
}

/* Prim Algorithm generates minimum spanning tree */
void MiniSpanTree_Prim(MGraph G)
{
	cout<<"Prim The algorithm generates a minimum spanning tree with the following results:"<<endl;
	int min,i,j,k;
	int adjvex[MAXVEX];
	int lowcost[MAXVEX];
	lowcost[0]=0;
	adjvex[0]=0;
	for(i=1;i<G.numVertexes;i++)
	{
		lowcost[i]=G.arc[0][i];
		adjvex[i]=0;
	}
	for(i=1;i<G.numVertexes;i++)
	{
		min=INFINITY;
		j=1;k=0;
		while(j<G.numVertexes)
		{
			if(lowcost[j]!=0 && lowcost[j]<min)
			{
				min=lowcost[j];
				k=j;
			}
			j++;
		}
		cout<<"("<<adjvex[k]<<","<<k<<")"<<endl;
		lowcost[k]=0;
		for(j=1;j<G.numVertexes;j++)
		{
			if(lowcost[j]!=0 && G.arc[k][j]<lowcost[j])
			{
				lowcost[j]=G.arc[k][j];
				adjvex[j]=k;
			}
		}
	}
	cout<<endl;
}

/* Kruskal Algorithm generates minimum spanning tree */

class Edge{		/*Definition of Edge Structure for Edge Set Array*/
public:
	int begin;
	int end;
	int weight;
};

void Swap(Edge *edges,int i,int j)		/* Exchange weights and head and tail */
{
	int temp;
	temp=edges[i].begin;
	edges[i].begin=edges[j].begin;
	edges[j].begin=temp;
	temp=edges[i].end;
	edges[i].end=edges[j].end;
	edges[j].end=temp;
	temp=edges[i].weight;
	edges[i].weight=edges[j].weight;
	edges[j].weight=temp;
}

void sort(Edge edges[],MGraph *G)		/* Sort weights */
{
	int i,j;
	for ( i=0;i<G->numEdges;i++)
	{
		for ( j=i+1;j<G->numEdges;j++)
		{
			if (edges[i].weight>edges[j].weight)
			{
				Swap(edges,i,j);
			}
		}
	}
	cout<<"After the weight order is:"<<endl;
	for (i=0;i<G->numEdges;i++)
	{
		cout<<"("<<edges[i].begin<<","<<edges[i].end<<")"<<endl;
	}
}

int Find(int *parent,int f)		/*Find the tail subscript of the vertex of a line*/
{
	while (parent[f]>0)
		f=parent[f];
	return f;
}

void MiniSpanTree_Kruskal(MGraph G)
{
	int i,j,n,m;
	Edge edges[MAXEDGE];
	int parent[MAXVEX];

	/*Convert adjacent array G to edges of edge set array and sort by weight from small to large*****BEGIN***********/
	int k=0;
	for ( i=0;i<G.numVertexes-1;i++)
	{
		for (j=i+1;j<G.numVertexes;j++)
		{
			if (G.arc[i][j]<INFINITY)
			{
				edges[k].begin=i;
				edges[k].end =j;
				edges[k].weight=G.arc[i][j];
				k++;
			}
		}
	}
	sort(edges, &G);
	/***************END***********************/

	for (i=0;i<G.numVertexes;i++)
		parent[i]=0;	/* Initialization array value is 0 */
	cout<<"Kruskal The algorithm generates a minimum spanning tree with the following results:"<<endl;
	for (i=0;i<G.numEdges;i++)	/* Cycle every edge */
	{
		n=Find(parent,edges[i].begin);
		m=Find(parent,edges[i].end);
		if (n!=m) /* If n and m are not equal, then there is no loop with the existing spanning tree on this side */
		{
			parent[n]=m;	/* Place the end vertex of this edge in the parent labeled as the starting point. */
							/* Indicates that this vertex is already in the spanning tree collection */
			cout<<"("<<edges[i].begin<<","<<edges[i].end<<") "<<edges[i].weight<<endl;
		}
	}
}

/* Dijkstra Algorithm for finding the shortest path P[V] and weighted length D[V] from V0 vertex of directed network G to the remaining vertices V*/
/*P[V]The value is the preceding vertex subscript, and D[V] represents the shortest path length from V0 to V and*/
void ShortestPath_Dijkstra(MGraph G, int V0, Patharc *P, ShortPathTable *D)
{
	int v,w,k,min;
	int final[MAXVEX];
	for(v = 0; v<G.numVertexes; v++)
	{
		final[v] = 0;
		(*D)[v] = G.arc[V0][v];
		(*P)[v] = V0;
	}
	(*D)[V0] = 0;
	final[V0] = 1;
	/*Start the main loop and find the shortest path from V0 to a V vertex each time*/
	for(v=0; v<V0; v++)
	{
		min = INFINITY;
		for(w=0; w<G.numVertexes; w++)
		{
			if(!final[w] && (*D)[w]<min)
			{
				k = w;
				min = (*D)[w];
			}
		}
		final[k] = 1;
		for (w=0; w<G.numVertexes; w++)		/*Correct current shortest path and distance*/
		{
			if(!final[w] && (min+G.arc[k][w]<(*D)[w]))
			{
				(*D)[w] = min+G.arc[k][w];
				(*P)[w] = k;
			}
		}
	}
	for(v=V0+1; v<G.numVertexes; v++)
	{
		min = INFINITY;
		for(w=0; w<G.numVertexes; w++)
		{
			if(!final[w] && (*D)[w]<min)
			{
				k = w;
				min = (*D)[w];
			}
		}
		final[k] = 1;
		for (w=0; w<G.numVertexes; w++)		/*Correct current shortest path and distance*/
		{
			if(!final[w] && (min+G.arc[k][w]<(*D)[w]))
			{
				(*D)[w] = min+G.arc[k][w];
				(*P)[w] = k;
			}
		}
	}

	cout<<"V"<<V0<<"The shortest path from a node to the remaining nodes is:"<<endl;
	for (w=0; w<G.numVertexes; w++)	
	{
		cout<<(*D)[w]<<"  ";
	}
	cout<<endl;
	cout<<"V"<<V0<<"The precursor nodes of the shortest path from the node to the remaining nodes are:"<<endl;
	for (w=0; w<G.numVertexes; w++)	
	{
		cout<<"V"<<(*P)[w]<<"  ";
	}
	cout<<endl;
}
/***********Dijkstra Algorithm End**********/

/*Floyd Algorithms for finding the shortest path P[V][W] and weighted length D[V][W] from each vertex V to the remaining vertices W in graph G*/
void ShortestPath_Floyd(MGraph G, Pathmatrix *P, ShortPathTable_Floyd *D)
{
	int v,w,k;
	for(v=0; v<G.numVertexes; ++v)	/*Initialize D and P*/
	{
		for(w=0; w<G.numVertexes; ++w)
		{
			(*D)[v][w] = G.arc[v][w];
			(*P)[v][w] = w;
		}
	}
	for(k=0; k<G.numVertexes; ++k)
	{
		for(v=0; v<G.numVertexes; ++v)
		{
			for(w=0; w<G.numVertexes; ++w)
			{
				if ((*D)[v][w]>(*D)[v][k]+(*D)[k][w])
				{
					(*D)[v][w] = (*D)[v][k]+(*D)[k][w];
					(*P)[v][w] = (*P)[v][k];
				}
			}
		}
	}

	for(v=0; v<G.numVertexes; ++v)	/*Output Shortest Path*/
	{
		for(w=v+1; w<G.numVertexes; w++)
		{
			cout<<"V"<<v<<"-V"<<w<<"The shortest distance is:"<<(*D)[v][w]<<endl;
			k = (*P)[v][w];
			cout<<"The path is: V"<<v;
			while(k!=w)
			{
				cout<<" -> V"<<k;
				k=(*P)[k][w];
			}
			cout<<" -> V"<<w<<endl;
		}
		cout<<endl;
	}
}
/***********Floyd Algorithm End**********/

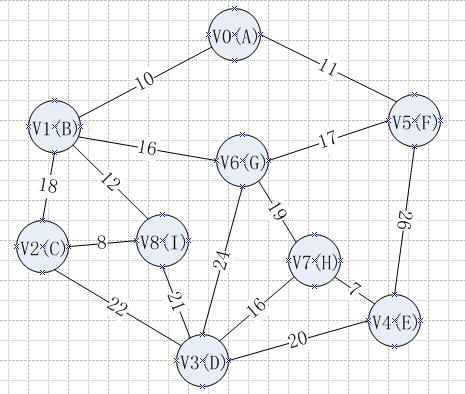
The code runs as follows:

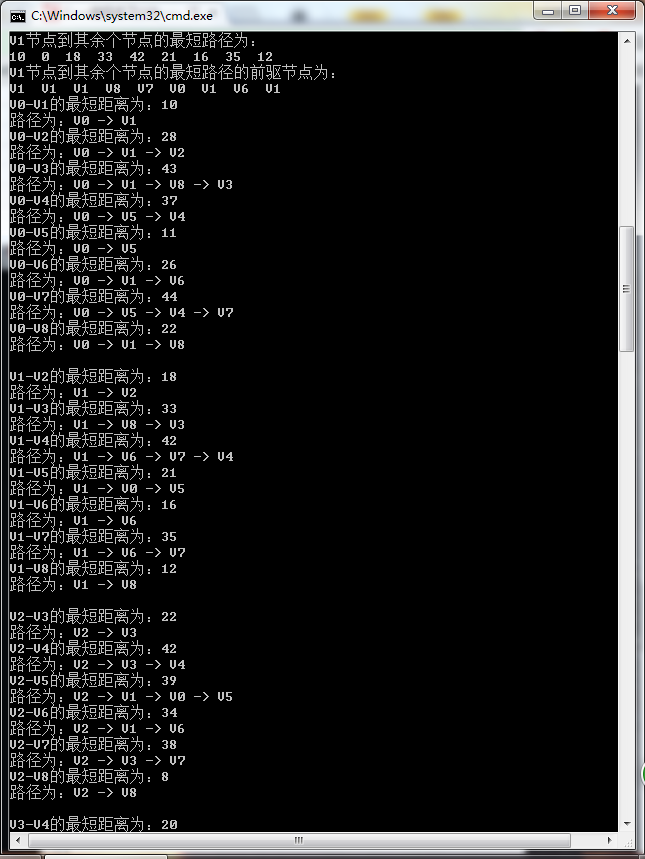
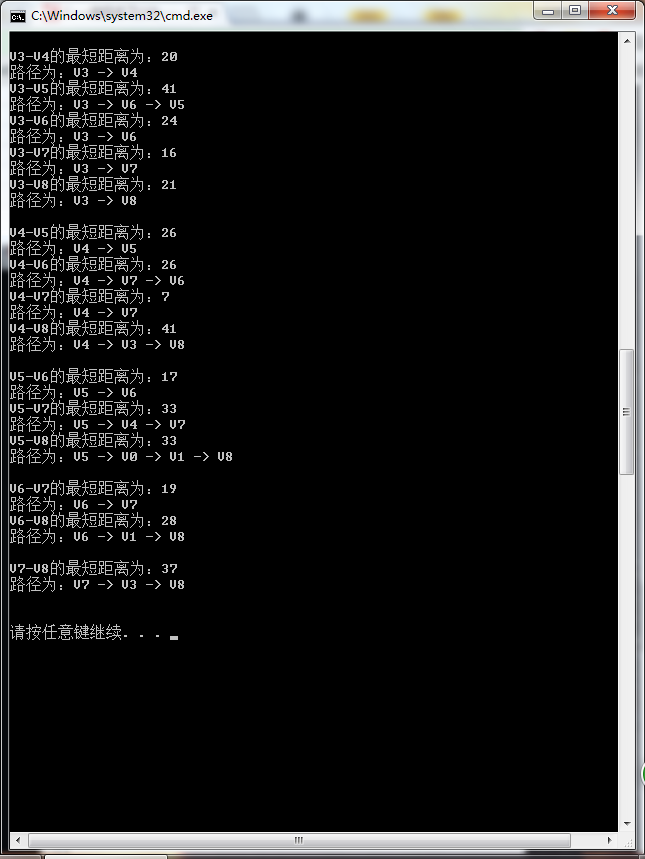
The results of the two algorithms are identical.