Water method test

Title 1: Small M cultured n colonies. Each colony has two attributes: quality and color. The colour can only be purple or red. Little M wanted to merge all the colonies into one colony. Because the merging process is very arduous, small M can only merge once a day, the whole process needs n-1 days. A merger turns two colonies into one. If the color of the original two colonies is the same, the two colonies will be fused, and the quality of the new colonies will be the sum of the original two colonies, and the color will not change. If the color of the original two colonies is different, the two colonies will fight. The quality of the new colonies is the difference between the quality of the original two colonies, and the color is the one with larger quality. Colony of bacteria. In particular, if a colony with a mass of 0 is produced in the intermediate process, the colony also needs to participate in the subsequent merger rather than be discarded directly; it can be proved that the colony with a mass of 0 is considered purple or red, which does not affect the subsequent calculation. At the end of each day's merger, Little M needs to feed every current colony. For a colony with a mass of w, small M spends w^2 units of energy feeding it for a day. Little M wants you to help him figure out the best order of colonies merging so that the total energy consumed by feeding is minimal. You just need to output the minimum energy you need.

It's a long topic, but it's very simple.

Consider the binary tree formed by combining two or two points at the beginning.

Establishment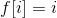If there is no father, then he is himself. At first nobody had a father.

If two points are to be merged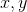So you need to make sure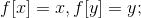When merging the two, order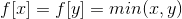All right.

With such an array of f, we can easily create the shape of the tree.

It's good to discuss this when we merge the colonies. We can think of the final f-sequence. There are one value of the first point and two values of the second point. Then you can have hash.

Memory search.

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;

int T,n;
long long dp[4037913],coef,a[11];
int fac[11],f[11];
int ty[4037913];
bool type[11];
char c[10];

long long dfs(int x){
	if(dp[coef] && ty[coef]==T) return dp[coef];
	if(x==n) return 0;
	long long mmin=1ll*1e18,tot=0,temp;
	int p[11];
	bool lt;
	p[0]=0;for(int i=1;i<=n;i++) if(f[i]==i) p[++p[0]]=i,tot+=a[i]*a[i];
	for(int i=1;i<=p[0];i++)
		for(int j=i+1;j<=p[0];j++) {
			lt=type[p[i]];temp=a[p[i]];tot-=a[p[i]]*a[p[i]]+a[p[j]]*a[p[j]];
			if(type[p[i]]==type[p[j]]) a[p[i]]=a[p[i]]+a[p[j]];
			else{
				if(a[p[i]]>a[p[j]]) a[p[i]]-=a[p[j]];
				else a[p[i]]=a[p[j]]-a[p[i]],type[p[i]]=type[p[j]];
			}
			coef=coef-1ll*p[j]*fac[p[j]-1]+1ll*p[i]*fac[p[j]-1];f[p[j]]=p[i];
			mmin=min(mmin,tot+a[p[i]]*a[p[i]]+dfs(x+1));
			a[p[i]]=temp;type[p[i]]=lt;
			coef=coef-1ll*p[i]*fac[p[j]-1]+1ll*p[j]*fac[p[j]-1];f[p[j]]=p[j];
			tot+=a[p[i]]*a[p[i]]+a[p[j]]*a[p[j]];
		}
	ty[coef]=T;
	return dp[coef]=mmin;
}

int main(){
	scanf("%d",&T);
	fac[0]=1;for(int i=1;i<=10;i++) fac[i]=fac[i-1]*i;fac[0]=0;
	while(T--){
		scanf("%d",&n);coef=0;
		for(int i=1;i<=n;i++){
			f[i]=i;coef+=f[i]*fac[i-1];
			scanf("%lld",&a[i]);
			scanf("%s",c);
			if(c[0]=='7') type[i]=false;
			else type[i]=true;
		}
		printf("%lld\n",dfs(1));
	}
}

Question 2: Pingping goes to the seaside for a holiday. There is a beautiful cobblestone beach on the seaside. Pingping picked up $n dollars of beautiful pebbles on the pebble beach and arranged them in a sequence. The beauty of the pebbles in the first place was a_i. Pingping wants to select a subsequence of pebbles from the original sequence, so that the beauty of the latter pebble in this subsequence is not lower than that of the former one. Pingping also wanted to know what the longest subsequence length he could get by doing so. Pingping thought about it and thought it was naive, so he decided to connect the cobblestone sequence to form a cobblestone ring, and then calculate the length of the longest subsequence that meets the requirements on the ring.

The longest nondescending subsequence of n times is obtained.

As long as the complexity is not full, we can pass this question.

The length of the longest ascending subsequence is the expectation because the data is guaranteed to be random..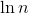

So when we slide the window, it's easy to add a dot after the sequence, but it's difficult to delete a dot before.

Direct rebuilding of violence is enough! Total refactoring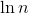Second, every refactoring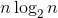. So the total time complexity is.

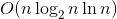There are a lot of water methods... It's really good because the data is random.

Question 3: Ping Ping Ping has a necklace. This necklace is strung with N beads, of which the energy value of a_i is on the first bead (a_i is not necessarily negative). For a continuous bead, Pingping defines its beauty as the sum of its energy values. Naturally, the beauty of a necklace is defined as the maximum beauty of all its successive segments. Pingping got a magic scissors. He could cut off exactly one continuous segment of the necklace, turn it over, and stitch it back together to get a new necklace. Pingping wants to use the scissors to get a new necklace with as much aesthetic value as possible. Then the question arises: Please tell Pingping what the maximum aesthetic value of his new necklace can be.

At that time, the examination was dull-witted. That's the last step.

First of all, if the number of positive numbers is <=1, you can output Top 2 directly.

Otherwise, consider that the answer must be the sum of the maximum two paragraphs.

Since this flip will definitely contribute to the answer, find the maximum two segments, and then flip the right endpoint of one segment + 1 to the right endpoint of another segment to get a continuous sequence.

For the sum of the maximum two segments in a ring, it must be the sum of the two segments in a sequence or the sum of the two segments minus the minimum.

That's all. Turn the problem into the sum of the two largest segments in the sequence, deal with the sum of the largest subsegments of a prefix directly, and then do it backwards.

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
using namespace std;

int n;
int a[200010];
long long f[200010],g[200010];
int t=0;
long long mmax=-1e18,tot,cmax;

long long solve(){
	long long ans=-1e18;
	for(int i=1;i<=n;i++) f[i]=max(f[i-1],0ll)+a[i],g[i]=max(g[i-1],f[i]);
	for(int i=n;i>=1;i--) f[i]=max(f[i+1],0ll)+a[i],ans=max(ans,f[i]+g[i-1]);
	return ans;
}

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]),t+=(a[i]>0),tot+=a[i];
		if(a[i]>mmax) cmax=mmax,mmax=a[i];
		else if(a[i]>cmax) cmax=a[i];
	}
	if(t<=1) {
		printf("%lld",mmax+cmax);
		return 0;
	}
	mmax=solve();
	for(int i=1;i<=n;i++) a[i]=-a[i];
	mmax=max(mmax,tot+solve());
	printf("%lld\n",mmax);
}

At that time, the exam was to figure out the sum of the maximum two paragraphs on the ring, and then O(n^2) rolled out directly.