I. Questions

• Question 1

  Scene: If your future mother-in-law asks you to give her one cent on the first day, two cents on the second day and four cents on the third day, and so on, twice as much as the previous day and one month (30 days) is enough.
  Question: How much is it for the 30th day and how much is it altogether?

• Question 2

  Scenario: If you have two jobs.
  First copy: 1 cent for you on the first day, 2 cents for you on the second day, 4 cents for you on the third day, and so on, twice as much as the previous day and one month (30 days).
  Part 2: You are paid 100,000 yuan a month.
  Question: Which salary is high? If you choose, do you want the first or the second?

2. Relevant hot search keywords

• How much does it cost to double a penny a day to thirty days later?
• One day, one cent, two days
• How much does it cost to double a dime a day for 30 days?
• One day, one cent, two days, two cents, three days, four cents
• One day, one cent, two days, two cents, two times as much as a month?
• What's the 30-day doubling of 0.01 per day?
• 0.01 How much is it at the end of the month to double every day?
• 0.01 doubled daily

3. Solving problems

Question 1 and Question 2 are the same in fact. Here the blogger introduces three different ways to solve the problem, namely, through the while loop, the power function combined with the general term sum formula of equal ratio series, and the recursive way of CTE common expression. You can refer to the script written by the blogger.

1. Use the while loop approach
   1.1 Look directly at the script and related comments:

   /*
       Author: Zhang 502219048
       Source of script: https://www.cnblogs.com/zhang502219048/p/11273639.html
       Function: The problem of calculating a penny doubled by one month through while loop
   */
   --Define variables
   declare @a decimal(18,2) = 0.01,   --@a How much is it per day, starting with day 1 0.01 element
           @total decimal(18,2) = 0,  --@total How much is the total for that day?
           @q int = 2,                --@q How many times a day
           @n int = 2,                --@n For the second day, and from the second day, because it was the second day that began to double.
           @nMax int = 30             --@nMax For the day of the last doubling
   
   --while Cycle, count to the 30th day, how much is the day and how much is the total amount as of that day
   while @n <= @nMax                  --Cycle from day 2 until day 30
   begin
       select @a = @a * @q            --How much is it for the day?
       select @total = @total + @a    --Calculate the total amount as of that day
       select @n = @n + 1             --Cyclic variables@n Add 1 day
   end
   
   --Output information
   print 'How much is the 30th day?'
   print @a
   print 'How much is the total cost for days 1 to 30?'
   print @total
   go

   1.2 Script Running Results:
   

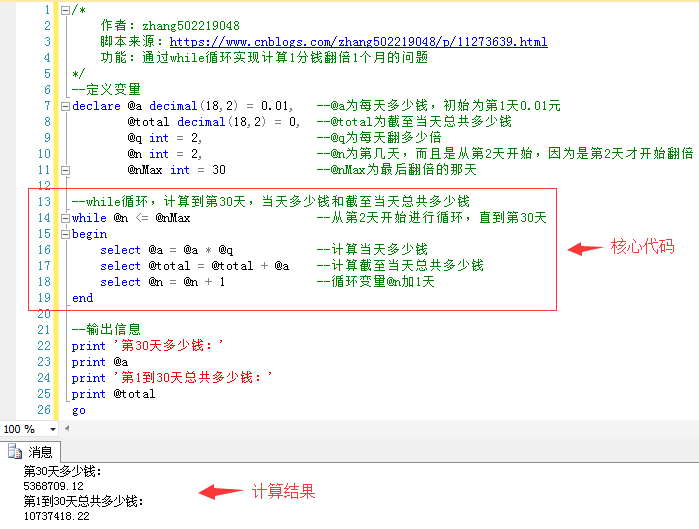
2. Sum Formula Using power Function and General Terms of Equal Ratio Sequence
   2.1 Let's first look at the general term formula and summation formula of equal-ratio series. Learn about them.
   
   2.2 Look directly at the script and related comments:

   /*
       Author: Zhang 502219048
       Source of script: https://www.cnblogs.com/zhang502219048/p/11273639.html
       Function: Through power function and sum formula of general terms of equal ratio series, the problem of calculating one penny and doubling one month can be realized.
   */
   --Define variables
   declare @a1 decimal(18,2) = 0.01,   --@a1 For Day 1 0.01 element
           @a30 decimal(18,2),         --@a30 How much is it for the 30th day?
           @total decimal(18,2),       --@total How much is the total for that day?
           @q int = 2,                 --@q How many times a day
           @n int = 30                 --@n For a total of several days
   
   --Use power How much is it on the 30th day by combining the general term formula of equal ratio series with the function?
   select @a30 = @a1 * power(@q, @n - 1)  --power(@q, @n - 1): Use power Function Computation@q Of@n - 1 Secondary power
   --Calculate the total amount of money as of the 30th day using the sum formula of equal ratio series
   select @total = (@a1 - @a30 * @q)/(1 - @q)
   
   --Output information
   print 'How much is the 30th day?'
   print @a30
   print 'How much is the total cost for days 1 to 30?'
   print @total
   go

   2.3 Script Running Results:
   

3. Using CTE Common Expression Recursion
   3.1 Look directly at the script and related comments:

   /*
       Author: Zhang 502219048
       Source of script: https://www.cnblogs.com/zhang502219048/p/11273639.html
       Function: Recursive CTE method is used to double one cent for one month.
       Field description: DayX for the day, MoneyX for the day how much, MoneyTotal for the day up to the total amount of money
   */
   
   with cte_table(DayX, MoneyX, MoneyTotal) as
   (
       select 1
           , cast(0.01 as decimal(18,2))  --Day 1 0.01 element
           , cast(0.01 as decimal(18,2))  --A total of 0 as of the first day.01 element
       union all
       select DayX + 1                                       --DayX Add 1 day
           , cast(MoneyX * 2 as decimal(18,2))               --The first DayX + 1 How much is it every day?
           , cast(MoneyTotal + MoneyX * 2 as decimal(18,2))  --Up to the end of the year DayX + 1 How much is the total for the day?
       from cte_table
       where DayX < 30  --Calculate to the 30th day, end the recursion
   )
   select * from cte_table  --View Detailed Data( DayX: Days; MoneyX: How much is it that day? MoneyTotal: How much is the total as of that day?
   go

   3.2 Script Running Results:
   

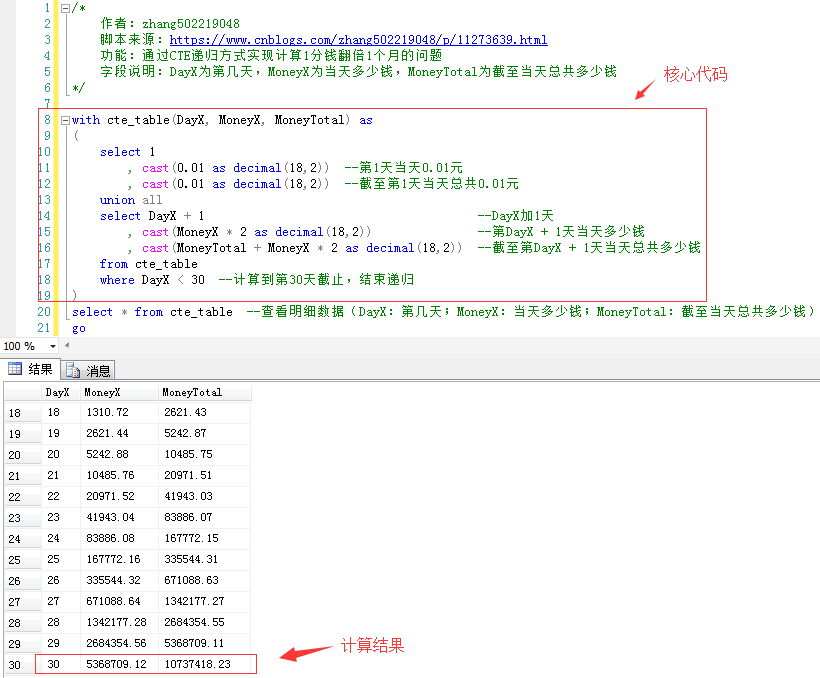
IV. CONCLUSION OF PROBLEMS

• Give 5,368,709.12 yuan (more than 5 million yuan) on the 30th day!
• As of the 30th day, the total amount was 10,737,418.23 yuan (more than 10 million yuan)!

V. Problem Expansion

• The Background Story of Equivalent Ratio Series: Chess Board Putting Grain, You can see it directly. Baidu Encyclopedia I will not elaborate on it here.
  
• CTE Common Expressions Generate Continuous Numbers or Dates. You can see another blog post written by the blogger.< sql server uses common table expression CTE to write general functions recursively to automatically generate continuous numbers and dates>
  

Author's statement

• You are welcome to reprint it, but it is important to indicate the source of the blog: https://www.cnblogs.com/zhang502219048/p/11273639.html