After we have learned RMQ, we know the principle of multiplication method, and use a power of two to maintain the interval length of each base 2. In fact, simply speaking, it is a merger problem. A 2 can be composed of two ones, and a 4 can be composed of two ones, and so on. So it's called multiplication. The multiplication method can usually be used to solve linear problems, such as the maximum value of the interval. When we fix the left endpoint, when the right endpoint moves continuously to the right, it is not difficult to find that the maximum value of the interval is monotonous.
Well, it's time to get back to the subject after all this nonsense.
Now, we ask the question, can we find the common ancestor of two points on the tree by multiplication?
For example, as shown in the figure, there are two nodes, X and Y. do we want to know their recent common ancestor?
Mark each node with serial number for later explanation:
So, we want to know the recent common ancestors of X and Y. we can make x rise one grid at a time and Y rise one grid at a time to see if their ancestors are the same.
[step 1] X will go to node 2, Y will go to node 3, find that they are different, and continue walking;
[step 2] X goes to 1, Y goes to 1, they are the same, quit, and find the nearest public ancestor.
It's easy to find that such an approach is O(N). But it can guarantee its correctness (when the depth of X and Y is different, it must first move the node with deep depth to the node with shallow depth)
Among them, we can make optimization. Because we can know that the more steps we take up, the more certain it will be. Similarly, we can use the multiplication method for maintenance.
Such a tree, for example.
When we first raise X to a point with the same depth as y, that is, X will go to point 4 (now X is at point 4), we will find that when X and Y go up 4 steps, they are empty, when they go up 2 steps, when they go up 1 step, they are node 3.
But for the previous picture, the upward step of X and Y is not the same. We can let them go up at the same time. Since then, we have introduced the multiplication method to find LCA (the nearest common ancestor).
LCA by multiplication method:
We can run dfs() once with the initial method of RMQ to find out who the father of each node is, record it to root[x][0], "X" is the current node, "root[x][0]" is the point (also known as the father node) obtained by the X node's step up.
Then, we know that father's father is grandfather, grandfather's grandfather is great grandfather? Zeng Zeng? , and so on. We can maintain the upwardness of each node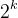
If it is beyond the scope of the tree, we make root[x][k] = 0. (if the sequence number of nodes on the tree is 1-N, this can not be done if it is 0-N-1)
How are the above practices maintained in code?
We write casually:
First, because the multiplier will be used, I will preprocess the log2() function first:
inline void Pre()
{
for(int i=0, j=0, nex = 2; i<maxN; i++)
{
if(i == nex) { nex <<= 1; j++; }
LOG[i] = j;
}
}And down again, we want to know that every point goes up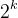Which node will be reached, so root[x][k] indicates that node x is up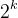Which node will step to.
void dfs(int u, int fa)
{
root[u][0] = fa;
deep[u] = deep[fa] + 1;
for(int i=0; (1 << (i + 1)) < N; i++) //Pretreatment part
{
root[u][i + 1] = root[root[u][i]][i];
}
for(int i=head[u], v; ~i; i=edge[i].nex)
{
v = edge[i].to;
if(v == fa) continue;
dfs(v, u);
}
}The deep array is used to record the depth, because we need to ensure the uniformity of depth.
Now, it's our LCA process:
inline int _LCA(int x, int y)
{
if(deep[x] < deep[y]) swap(x, y);
int det = deep[x] - deep[y]; //Convert the depth difference into binary form
for(int i=LOG[det]; i>=0; i--)
{
if((det >> i) & 1) x = root[x][i];
}
if(x == y) return x; //Sometimes, they are actually two points with different depths in a chain
for(int i=LOG[N]; i>=0; i--)
{
if(root[x][i] ^ root[y][i]) //When encountering different situations, we will go up and approach the real answer continuously, but it will not be the same, just infinite approach
{
x = root[x][i];
y = root[y][i];
}
}
return root[x][0];
}It is an infinite approximation, but it will never be the same process, so the final return is root[x][0], because the minimum approximation unit is 1, we only need to be approximation, so at this time, the nearest common ancestor of X and Y must be their previous unit. But first of all, we need to exclude that when we put them at the same depth, they are already overlapped.
The whole process:
dfs(gen, 0); //Root node
int x, y;
scanf("%d%d", &x, &y);
printf("%d\n", _LCA(x, y));It's a sequence like this.
Put a template question:
Nearest Common Ancestors
#include <iostream>
#include <cstdio>
#include <cmath>
#include <string>
#include <cstring>
#include <algorithm>
#include <limits>
#include <vector>
#include <stack>
#include <queue>
#include <set>
#include <map>
#include <bitset>
//#include <unordered_map>
//#include <unordered_set>
#define lowbit(x) ( x&(-x) )
#define pi 3.141592653589793
#define e 2.718281828459045
#define INF 0x3f3f3f3f3f3f3f3f
//#define INF 10000007.
#define eps 1e-7
#define HalF (l + r)>>1
#define lsn rt<<1
#define rsn rt<<1|1
#define Lson lsn, l, mid
#define Rson rsn, mid+1, r
#define QL Lson, ql, qr
#define QR Rson, ql, qr
#define myself rt, l, r
#define MP(a, b) make_pair(a, b)
using namespace std;
typedef unsigned long long ull;
typedef unsigned int uit;
typedef long long ll;
const int maxN = 1e4 + 7;
int N, head[maxN], cnt, du[maxN], gen, root[maxN][20], deep[maxN], LOG[maxN];
struct Eddge
{
int nex, to;
Eddge(int a=-1, int b=0):nex(a), to(b) {}
}edge[maxN << 1];
inline void addEddge(int u, int v)
{
edge[cnt] = Eddge(head[u], v);
head[u] = cnt++;
}
inline void _add(int u, int v) { addEddge(u, v); addEddge(v, u); }
void dfs(int u, int fa)
{
root[u][0] = fa;
deep[u] = deep[fa] + 1;
for(int i=0; (1 << (i + 1)) < N; i++) //Pretreatment part
{
root[u][i + 1] = root[root[u][i]][i];
}
for(int i=head[u], v; ~i; i=edge[i].nex)
{
v = edge[i].to;
if(v == fa) continue;
dfs(v, u);
}
}
inline int _LCA(int x, int y)
{
if(deep[x] < deep[y]) swap(x, y);
int det = deep[x] - deep[y]; //Convert the depth difference into binary form
for(int i=LOG[det]; i>=0; i--)
{
if((det >> i) & 1) x = root[x][i];
}
if(x == y) return x; //Sometimes, they are actually two points with different depths in a chain
for(int i=LOG[N]; i>=0; i--)
{
if(root[x][i] ^ root[y][i]) //When encountering different situations, we will go up and approach the real answer continuously, but it will not be the same, just infinite approach
{
x = root[x][i];
y = root[y][i];
}
}
return root[x][0];
}
inline void init()
{
cnt = 0;
for(int i=1; i<=N; i++)
{
du[i] = 0;
head[i] = -1;
}
}
inline void Pre()
{
for(int i=0, j=0, nex = 2; i<maxN; i++)
{
if(i == nex) { nex <<= 1; j++; }
LOG[i] = j;
}
}
int main()
{
Pre();
int T; scanf("%d", &T); deep[0] = 0;
while(T--)
{
scanf("%d", &N);
init();
for(int i=1, u, v; i<N; i++)
{
scanf("%d%d", &u, &v);
addEddge(u, v); du[v]++;
}
for(int i=1; i<=N; i++) if(!du[i]) { gen = i; break; }
dfs(gen, 0); //Root node
int x, y;
scanf("%d%d", &x, &y);
printf("%d\n", _LCA(x, y));
}
return 0;
}
Written in the end
After learning the multiplication method to find LCA, we need to know that multiplication is not a template, but a way of thinking. It can play a very effective optimization role in maintaining the linear relationship.
