This paper will first introduce what is heap, then introduce the insert and delete operation of heap, and finally give the code implementation of heap and test it.

What is a heap?

A heap is a complete binary tree. The value of a node in the heap is always no greater than or no less than the value of its parent node. The heap with the largest root node is called the large root heap, and the heap with the smallest root node is called the small root heap.
First, we explain what a complete binary tree is. Let the depth of a binary tree be H. except for the H layer, the number of nodes in all other layers (1-h-1) reaches the maximum. All nodes in the H layer are continuously concentrated on the left. This is a complete binary tree. As shown in the figure below, the binary tree on the left meets the definition of a complete binary tree, while the one on the right does not.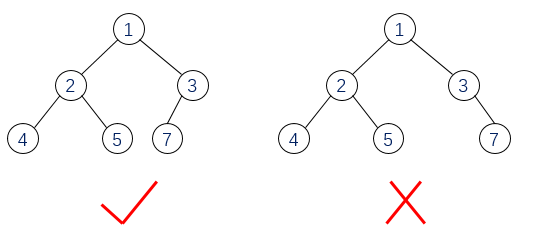

On the left side of the figure above is a small root heap, which satisfies that the value of any node is always no less than that of its parent node.

Stack representation

In the general binary tree representation, the node structure needs to be defined first. The node contains a pointer to the parent node, as shown below:

class Node<E>{
		E e;//Node stored value
		Node left,right;//Left and right child nodes
		public Node(E e){
			this.e = e;
			this.left = this.right = null;
		}
	}

But the heap is not stored like a tree. Instead of using a parent or child pointer, it is implemented by an array. How to use array to realize it? First look at a picture, as follows: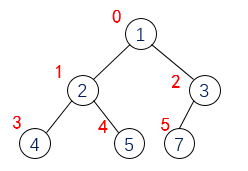

We start from 0 to number the nodes and find the corresponding relationship between the indexes of the parent and child nodes.
First, the index of the parent node is found by the index of the child node. If the index of the child node is i, the index of the parent node is

int parentIndex = (i - 1) / 2;

Then, the index of the child node is found through the index of the parent node. If the index of the parent node is set to p, the index of its child node is

int leftChildIndex  = 2 * p + 1;//Left child node
int rightChildIndex = 2 * p + 2;//Right child node

In this way, through the index relationship between the child node and the parent node, it is equivalent to establishing the pointer between the parent node and the child node, and realizing the data structure of using array to store the heap.

Heap insertion

For the heap, there are only two operations: insert and delete. Let's talk about the insert operation of the heap first. Here, take the small root heap as an example.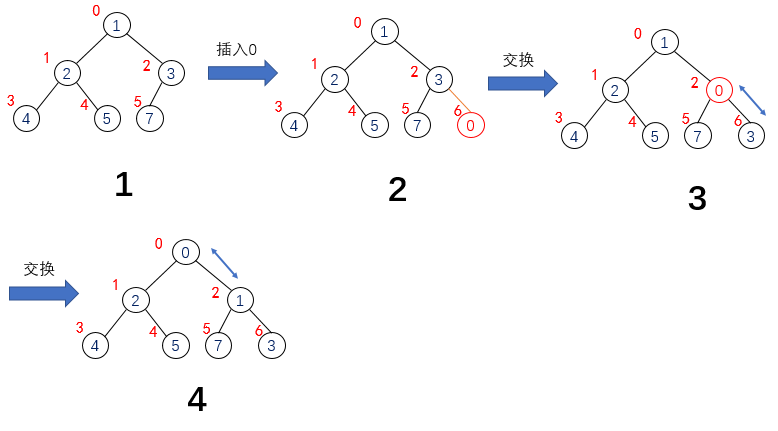

As shown in Figure 1 above, insert element 0 into the small root heap, first place the element at the end of the last line of the binary tree, and it is still a complete binary tree at this time; then compare the value of the element with that of the parent node, if the value of the modified node is less than that of the parent node, exchange it, as shown in Figure 3; then compare and exchange it with the parent node again, until the value of the node is greater than or equal to that of the parent node Or it is the root node, as shown in Figure 4. The heap still meets the definition.

Deletion of heap

For the heap, deleting an element means removing the root node. Taking the small root heap as an example, it refers to removing the minimum node in the root, that is, the root node. It's easy to remove. After that, we need to make the heap still meet the definition.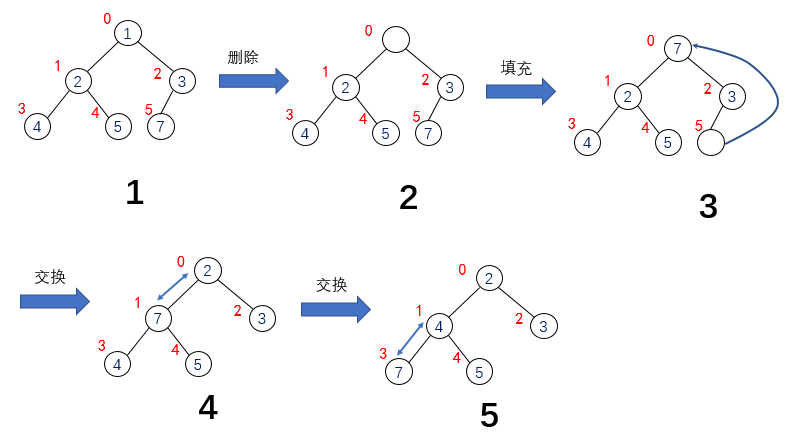

First, delete the index 0 in the heap, that is, the root node, which is the minimum value for the small root heap. Then fill the last element in the heap to the root node, as shown in Figure 3; then compare the node with the left and right child nodes; if the node is larger than the value of the smaller node in the left and right child nodes, exchange with the node (the parent node in the small root heap will always exchange with the smaller child node in the left and right child nodes), as shown in Figure 4 and figure 5; until the value of the node is less than The value of its left and right child nodes or the left and right child nodes of the node are empty. The heap still meets the definition.

Implementation of heap

The following shows the code implementation of the heap, as shown below, which implements the insertion and deletion of the heap and tests it.

package datastructures;

public class Heap {
	private int[] data;//Array of storage heap
	private int size;//Number of elements in the heap
	public Heap(int capacity){
		data = new int[capacity];//Initialize array
		size = 0;//Number of initializations
	}

	/**
	 * Insertion element
	 */
	public void insert(int value) throws Exception{
		if(size == data.length)
			throw new Exception("Heap full");
		else{
			data[size] = value;//Place the newly inserted element at the end of the heap
			int i = size;
			size ++;
			while(i > 0){//Adjust the heap until the conditions are met
				int p = (i - 1) / 2;
				if(data[i] < data[p]){
					int temp = data[i];
					data[i] = data[p];
					data[p] = temp;
					i = p;
				}
				else
					break;
			}
		}
	}
	
	/**
	 * Delete elements in the heap
	 * @return
	 * @throws Exception
	 */
	public int delMin() throws Exception{
		int res;
		if(size == 0)
			throw new Exception("Empty");
		else{
			res = data[0];//Return element with index 0
			size -- ;
			data[0] = data[size];//Fill the last element in the heap to the position with index 0
			int i = 0;
			while(2 * i + 1 < size){//Adjust the heap
				int left = 2 * i + 1;
				int right = 2 * i + 2;
				if(right < size && data[right] < data[left] && data[right] < data[i]){
					int temp = data[i];
					data[i] = data[right];
					data[right] = temp;
					i = right;
				}
				else if(data[left] < data[i] && (right >= size || data[right] >= data[left])){
					int temp = data[i];
					data[i] = data[left];
					data[left] = temp;
					i = left;
				}
				else
					break;
			}
		}
		return res;
	}
	
	//test
	public static void main(String[] args) throws Exception {
		Heap heap = new Heap(10);
		heap.insert(1);
		heap.insert(5);
		heap.insert(4);
		heap.insert(3);
		heap.insert(6);
		heap.insert(2);
		System.out.println(heap.delMin());
		System.out.println(heap.delMin());
		System.out.println(heap.delMin());
		System.out.println(heap.delMin());
		System.out.println(heap.delMin());
		System.out.println(heap.delMin());
	}
	
}

Recommended reading
Why are there red and black trees? What is a red black tree? After reading this, you will understand
What are B-trees and B + trees in the data structure series? Why can't binary search trees work?
It's 2020. I heard you won't merge and rank? Hand to hand to teach you the sorting algorithm of handwriting merging
Why are there multiple threads? What is thread safety? How to ensure thread safety?