Preface

In this paper, the gradient algorithm and the improved random gradient algorithm are compared, and their advantages and disadvantages are summarized, and sklearn.linear'u model.logistic regression is introduced in detail.

Two improved random gradient rising algorithm

The gradient rise algorithm needs to traverse the whole data set every time it updates the regression coefficient (optimal parameter). Let's take a look at the gradient rise algorithm we wrote earlier:

def gradAscent(dataMatIn, classLabels):
    dataMatrix = np.mat(dataMatIn)                                        #mat converted to numpy
    labelMat = np.mat(classLabels).transpose()                            #Convert to numpy's mat and transpose
    m, n = np.shape(dataMatrix)                                            #Returns the size of the dataMatrix. m is the number of rows and n is the number of columns.
    alpha = 0.01                                                        #The moving step, that is, the learning rate, controls the magnitude of the update.
    maxCycles = 500                                                        #Maximum number of iterations
    weights = np.ones((n,1))
    for k in range(maxCycles):
        h = sigmoid(dataMatrix * weights)                                #Vectorization formula of gradient rise
        error = labelMat - h
        weights = weights + alpha * dataMatrix.transpose() * error
    return weights.getA(),weights_array                                    #Convert matrix to array, return weight array

Suppose we use a dataset of 100 samples. So, dataMatrix is a 100 * 3 matrix. Every time h is calculated, the matrix multiplication of dataMatrix*weights needs to be calculated, with 100 * 3 times of multiplication and 100 * 2 times of addition. In the same way, when updating the weight of regression coefficient (optimal parameter), the whole data set is also needed, and matrix multiplication is needed. All in all, this method is feasible for processing about 100 datasets, but if there are billions of samples and thousands of features, the computational complexity of this method is too high. Therefore, we need to improve the algorithm. When we update the regression coefficient (optimal parameter), can we not use all samples? Only one sample point at a time to update the regression coefficient (optimal parameter)? This can effectively reduce the amount of computation, this method is called the random gradient rise algorithm.

1 random gradient rising algorithm

Let's look directly at the code:

# Random gradient rising algorithm
def stocGradAscent0(dataMatrix, classLabels):
    dataArr=np.array(dataMatrix)
    m, n = np.shape(dataArr)
    alpha = 0.01
    weights = np.ones(n)  # initialize to all ones
    for i in range(m):
        # h. Errors are all numerical values, and there is no matrix conversion process.
        h = sigmoid(sum(dataArr[i] * weights))
        error = classLabels[i] - h
        weights = weights + alpha * error * dataArr[i]
    return weights

Improvement of random gradient algorithm:

# Improvement of random gradient rising algorithm
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    dataArr=np.array(dataMatrix)
    m, n = np.shape(dataArr)
    weights = np.ones(n)  #Parameter initialization
    for j in range(numIter):
        dataIndex = list(range(m))
        for i in range(m):
            alpha = 4 / (1.0 + j + i) + 0.0001  #Decrease the size of alpha by 1/(j+i) at a time.
            randIndex = int(np.random.uniform(0, len(dataIndex)))  # Random sampling to change the sampling sample and reduce the periodic fluctuation
            h = sigmoid(sum(dataArr[randIndex] * weights))      # Select a randomly selected sample and calculate h
            error = classLabels[randIndex] - h                  # calculation error
            weights = weights + alpha * error * dataArr[randIndex] # Update regression coefficient
            del (dataIndex[randIndex])                             # Delete used samples
    return weights

The first improvement of this algorithm is that alpha will adjust every iteration, and although alpha will decrease with the number of iterations, it will never decrease to 0, because there is still a constant term. The reason why this has to be done is to ensure that the new data still has some impact after many iterations. If the problem that needs to be dealt with is dynamic, the above constant term can be appropriately increased to ensure that the new value gets a larger regression coefficient. It is also worth noting that in the function of decreasing alpha, alpha is reduced by 1/(j+i) at a time, where j is the number of iterations and i is the subscript of the sample point. The second improvement is to use only one sample point when updating the regression coefficient (optimal parameter), and the selected sample point is random, and the used sample point is not used in each iteration. This method can effectively reduce the amount of calculation and ensure the regression effect.

Write the following code to see the classification effect of the improved random gradient rise algorithm:
 

# -*- coding: UTF-8 -*-
import matplotlib.pyplot as plt
import numpy as np

"""
//Function Description: load data
Parameters:
    //nothing
Returns:
    dataMat - Data list
    labelMat - Tag list
Author:
    yangshaojun
Modify:
    2020-02-01
"""


# The first feature is usually w0 when the loading data feature changes to 3D
def loadDataSet():
    dataMat = []  # This list stores features
    labelMat = []  # Label this list
    fr = open('testSet.txt')  # Open file
    for line in fr.readlines():  # Read by line
        lineArr = line.strip().split('\t')  # Go to enter and put it in the list
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])  # Each sample feature is stored as a list
        labelMat.append(int(lineArr[2]))  # Add to label list
    fr.close()  # Close file
    return dataMat, labelMat  # Return


"""
//Function Description: drawing datasets
Parameters:
    //nothing
Returns:
    //nothing
Author:
    yangshaojun
Modify:
    2020-02-01
"""
def plotDataSet():
    dataMat, labelMat = loadDataSet()
    dataArr = np.array(dataMat)  # Array array converted to numpy
    n = np.shape(dataArr)[0]  # Number of data samples
    xcode1 = []; ycode1 = []  #Positive samples
    xcode2 = []; ycode2 = []  #Negative sample
    for i in range(n):        #Classify by dataset label
        if int(labelMat[i]) == 1:
            xcode1.append(dataArr[i, 1]); ycode1.append(dataArr[i, 2]) #1 is a positive sample
        else:
            xcode2.append(dataArr[i, 1]); ycode2.append(dataArr[i, 2]) #0 is a negative sample
    fig = plt.figure()
    ax = fig.add_subplot(111) #Add subplot
    ax.scatter(xcode1, ycode1, s=20, c='red', marker='s', alpha=0.5) #Draw positive sample
    ax.scatter(xcode2, ycode2, s=20, c='green', alpha=0.5) #Draw negative sample
    plt.title('DataSet') #Drawing title
    plt.xlabel('x')  #Drawing label
    plt.ylabel('y')
    plt.show()  #display

"""
//Function Description: sigmoid function
Parameters:
    inX - data
Returns:
    sigmoid function
Author:
    yangshaojun     
"""
def sigmoid(inX):
    return 1.0 / (1 + np.exp(-inX))

"""
//Function Description: gradient rise algorithm

Parameters:
    dataMatIn - data set
    classLabels - Data labels
Returns:
    weights.getA() - Weight array obtained(Optimal parameters)
    [[ 4.12414349]
    [ 0.48007329]
    [-0.6168482 ]]
Author:
    yangshaojun
Modify:
    2020-02-01
"""
def gradAscent(dataMatIn, classLabels):
    dataMatrix = np.mat(dataMatIn)  # List to numpy mat 100 row 3 column
    labelMat = np.mat(classLabels).transpose() #Convert to numpy's mat and transpose 100 rows and 1 column
    m, n = np.shape(dataMatrix)  # Returns the size of the dataMatrix. m is the number of rows and n is the number of columns.
    alpha = 0.001  #The moving step, that is, the learning rate, controls the magnitude of the update.
    maxCycles = 500  # Maximum number of iterations
    weights = np.ones((n, 1))  # Create a matrix element of 3 rows and 1 column as 1
    for k in range(maxCycles):
        h = sigmoid(dataMatrix * weights)  #Vectorization formula of gradient rise
        error = (labelMat - h)
        weights = weights + alpha * dataMatrix.transpose() * error
    return weights.getA()  # Convert matrix to array, return weight array

"""
//Function Description: drawing datasets

Parameters:
    weights - Weight parameter array
Returns:
    //nothing
Author:
    yangshaojun
Modify:
    2020-02-01
"""

def plotBestFit(weights):
    dataMat, labelMat = loadDataSet()
    dataArr = np.array(dataMat)  #Array array converted to numpy
    n = np.shape(dataArr)[0]  # Number of returned samples
    xcode1 = []; ycode1 = []  #Positive samples
    xcode2 = []; ycode2 = []  #Negative sample
    for i in range(n):        #Classify by dataset label
        if int(labelMat[i]) == 1:
            xcode1.append(dataArr[i, 1]);  ycode1.append(dataArr[i, 2]) #1 is a positive sample
        else:
            xcode2.append(dataArr[i, 1]);  ycode2.append(dataArr[i, 2]) #0 is a negative sample
    fig = plt.figure()
    ax = fig.add_subplot(111)                                           #Add subplot
    ax.scatter(xcode1, ycode1, s=30, c='red', marker='s')               #Draw positive sample
    ax.scatter(xcode2, ycode2, s=30, c='green')                         #Draw negative sample
    x = np.arange(-3.0, 3.0, 0.1)
    y = (-weights[0] - weights[1] * x) / weights[2]  # The value of y here is x2
    ax.plot(x, y)
    plt.xlabel('X1');
    plt.ylabel('X2');
    plt.show()


# Random gradient rising algorithm
def stocGradAscent0(dataMatrix, classLabels):
    dataArr=np.array(dataMatrix)
    m, n = np.shape(dataArr)
    alpha = 0.01
    weights = np.ones(n)  # initialize to all ones
    for i in range(m):
        # h. Errors are all numerical values, and there is no matrix conversion process.
        h = sigmoid(sum(dataArr[i] * weights))
        error = classLabels[i] - h
        weights = weights + alpha * error * dataArr[i]
    return weights


# Improvement of random gradient rising algorithm
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    dataArr=np.array(dataMatrix)
    m, n = np.shape(dataArr)
    weights = np.ones(n)  #Parameter initialization
    for j in range(numIter):
        dataIndex = list(range(m))
        for i in range(m):
            alpha = 4 / (1.0 + j + i) + 0.0001  #Decrease the size of alpha by 1/(j+i) at a time.
            randIndex = int(np.random.uniform(0, len(dataIndex)))  # Random sampling to change the sampling sample and reduce the periodic fluctuation
            h = sigmoid(sum(dataArr[randIndex] * weights))      # Select a randomly selected sample and calculate h
            error = classLabels[randIndex] - h                  # calculation error
            weights = weights + alpha * error * dataArr[randIndex] # Update regression coefficient
            del (dataIndex[randIndex])                             # Delete used samples
    return weights



if __name__ == '__main__':
    dataArr, labelMat = loadDataSet()
    weights = stocGradAscent1(dataArr, labelMat)
    plotBestFit(weights)

Code run result:

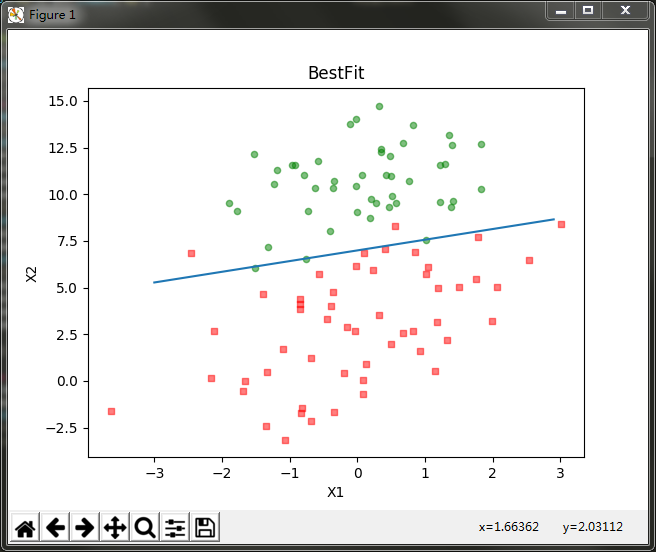
The relationship between the regression coefficient and the number of iterations

It can be seen that the classification effect is also good. However, from this classification result, we can not easily see the relationship between the number of iterations and the regression coefficient, nor can we directly see the convergence of each regression method. Therefore, we write a program to draw the relationship curve between regression coefficient and the number of iterations:

# -*- coding:UTF-8 -*-
from matplotlib.font_manager import FontProperties
import matplotlib.pyplot as plt
import numpy as np
import random


"""
//Function Description: load data

Parameters:
    //nothing
Returns:
    dataMat - Data list
    labelMat - Tag list

"""
def loadDataSet():
    dataMat = []                                                        #Create data list
    labelMat = []                                                        #Create label list
    fr = open('testSet.txt')                                            #Open file   
    for line in fr.readlines():                                            #Read by line
        lineArr = line.strip().split()                                    #Go to enter and put it in the list
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])        #Add data
        labelMat.append(int(lineArr[2]))                                #Add tags
    fr.close()                                                            #Close file
    return dataMat, labelMat                                            #Return

"""
//Function Description: sigmoid function

Parameters:
    inX - data
Returns:
    sigmoid function

"""
def sigmoid(inX):
    return 1.0 / (1 + np.exp(-inX))

"""
//Function Description: gradient rise algorithm

Parameters:
    dataMatIn - data set
    classLabels - Data labels
Returns:
    weights.getA() - Weight array obtained(Optimal parameters)
    weights_array - Regression coefficient per update

"""
def gradAscent(dataMatIn, classLabels):
    dataMatrix = np.mat(dataMatIn)                                        #mat converted to numpy
    labelMat = np.mat(classLabels).transpose()                            #Convert to numpy's mat and transpose
    m, n = np.shape(dataMatrix)                                            #Returns the size of the dataMatrix. m is the number of rows and n is the number of columns.
    alpha = 0.01                                                        #The moving step, that is, the learning rate, controls the magnitude of the update.
    maxCycles = 500                                                        #Maximum number of iterations
    weights = np.ones((n,1))
    weights_array = np.array([])
    for k in range(maxCycles):
        h = sigmoid(dataMatrix * weights)                                #Vectorization formula of gradient rise
        error = labelMat - h
        weights = weights + alpha * dataMatrix.transpose() * error
        weights_array = np.append(weights_array,weights)
    weights_array = weights_array.reshape(maxCycles,n)
    return weights.getA(),weights_array                                    #Converts a matrix to an array and returns



"""
//Function Description: improved random gradient rising algorithm

Parameters:
    dataMatrix - Data array
    classLabels - Data labels
    numIter - Iteration times
Returns:
    weights - Obtained regression coefficient array(Optimal parameters)
    weights_array - Regression coefficient per update

"""
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    m,n = np.shape(dataMatrix)                                                #Returns the size of the dataMatrix. m is the number of rows and n is the number of columns.
    weights = np.ones(n)                                                       #Parameter initialization
    weights_array = np.array([])                                            #Store regression coefficients for each update
    for j in range(numIter):                                           
        dataIndex = list(range(m))
        for i in range(m):           
            alpha = 4/(1.0+j+i)+0.01                                            #Decrease the size of alpha by 1/(j+i) at a time.
            randIndex = int(random.uniform(0,len(dataIndex)))                #Randomly selected samples
            h = sigmoid(sum(dataMatrix[randIndex]*weights))                    #Select a randomly selected sample and calculate h
            error = classLabels[randIndex] - h                                 #calculation error
            weights = weights + alpha * error * dataMatrix[randIndex]       #Update regression coefficient
            weights_array = np.append(weights_array,weights,axis=0)         #Add regression coefficient to array
            del(dataIndex[randIndex])                                         #Delete used samples
    weights_array = weights_array.reshape(numIter*m,n)                         #Changing dimensions
    return weights,weights_array                                             #Return

"""
//Function Description: draw the relationship between regression coefficient and iteration times

Parameters:
    weights_array1 - Regression coefficient array 1
    weights_array2 - Regression coefficient array 2
Returns:
    //nothing
"""
def plotWeights(weights_array1,weights_array2):
    #Format Chinese characters
    font = FontProperties(fname=r"c:\windows\fonts\simsun.ttc", size=14)
    #Divide the fig canvas into 1 row and 1 column without sharing the x-axis and y-axis. The size of the fig canvas is (13,8)
    #When nrow = 3 and nclos = 2, it means that the fig canvas is divided into six regions, and axs[0][0] means the first row and the first column
    fig, axs = plt.subplots(nrows=3, ncols=2,sharex=False, sharey=False, figsize=(20,10))
    x1 = np.arange(0, len(weights_array1), 1)
    #Draw the relationship between w0 and the number of iterations
    axs[0][0].plot(x1,weights_array1[:,0])
    axs0_title_text = axs[0][0].set_title(u'Gradient rise algorithm: relationship between regression coefficient and iteration times',FontProperties=font)
    axs0_ylabel_text = axs[0][0].set_ylabel(u'W0',FontProperties=font)
    plt.setp(axs0_title_text, size=20, weight='bold', color='black') 
    plt.setp(axs0_ylabel_text, size=20, weight='bold', color='black')
    #Draw the relationship between w1 and the number of iterations
    axs[1][0].plot(x1,weights_array1[:,1])
    axs1_ylabel_text = axs[1][0].set_ylabel(u'W1',FontProperties=font)
    plt.setp(axs1_ylabel_text, size=20, weight='bold', color='black')
    #Drawing the relationship between w2 and the number of iterations
    axs[2][0].plot(x1,weights_array1[:,2])
    axs2_xlabel_text = axs[2][0].set_xlabel(u'Iteration times',FontProperties=font)
    axs2_ylabel_text = axs[2][0].set_ylabel(u'W1',FontProperties=font)
    plt.setp(axs2_xlabel_text, size=20, weight='bold', color='black') 
    plt.setp(axs2_ylabel_text, size=20, weight='bold', color='black')


    x2 = np.arange(0, len(weights_array2), 1)
    #Draw the relationship between w0 and the number of iterations
    axs[0][1].plot(x2,weights_array2[:,0])
    axs0_title_text = axs[0][1].set_title(u'Improved random gradient rising algorithm: the relationship between regression coefficient and iteration number',FontProperties=font)
    axs0_ylabel_text = axs[0][1].set_ylabel(u'W0',FontProperties=font)
    plt.setp(axs0_title_text, size=20, weight='bold', color='black') 
    plt.setp(axs0_ylabel_text, size=20, weight='bold', color='black')
    #Draw the relationship between w1 and the number of iterations
    axs[1][1].plot(x2,weights_array2[:,1])
    axs1_ylabel_text = axs[1][1].set_ylabel(u'W1',FontProperties=font)
    plt.setp(axs1_ylabel_text, size=20, weight='bold', color='black')
    #Drawing the relationship between w2 and the number of iterations
    axs[2][1].plot(x2,weights_array2[:,2])
    axs2_xlabel_text = axs[2][1].set_xlabel(u'Iteration times',FontProperties=font)
    axs2_ylabel_text = axs[2][1].set_ylabel(u'W1',FontProperties=font)
    plt.setp(axs2_xlabel_text, size=20, weight='bold', color='black') 
    plt.setp(axs2_ylabel_text, size=20, weight='bold', color='black')

    plt.show()       

if __name__ == '__main__':
    dataMat, labelMat = loadDataSet()           
    weights1,weights_array1 = stocGradAscent1(np.array(dataMat), labelMat)

    weights2,weights_array2 = gradAscent(dataMat, labelMat)
    plotWeights(weights_array1, weights_array2)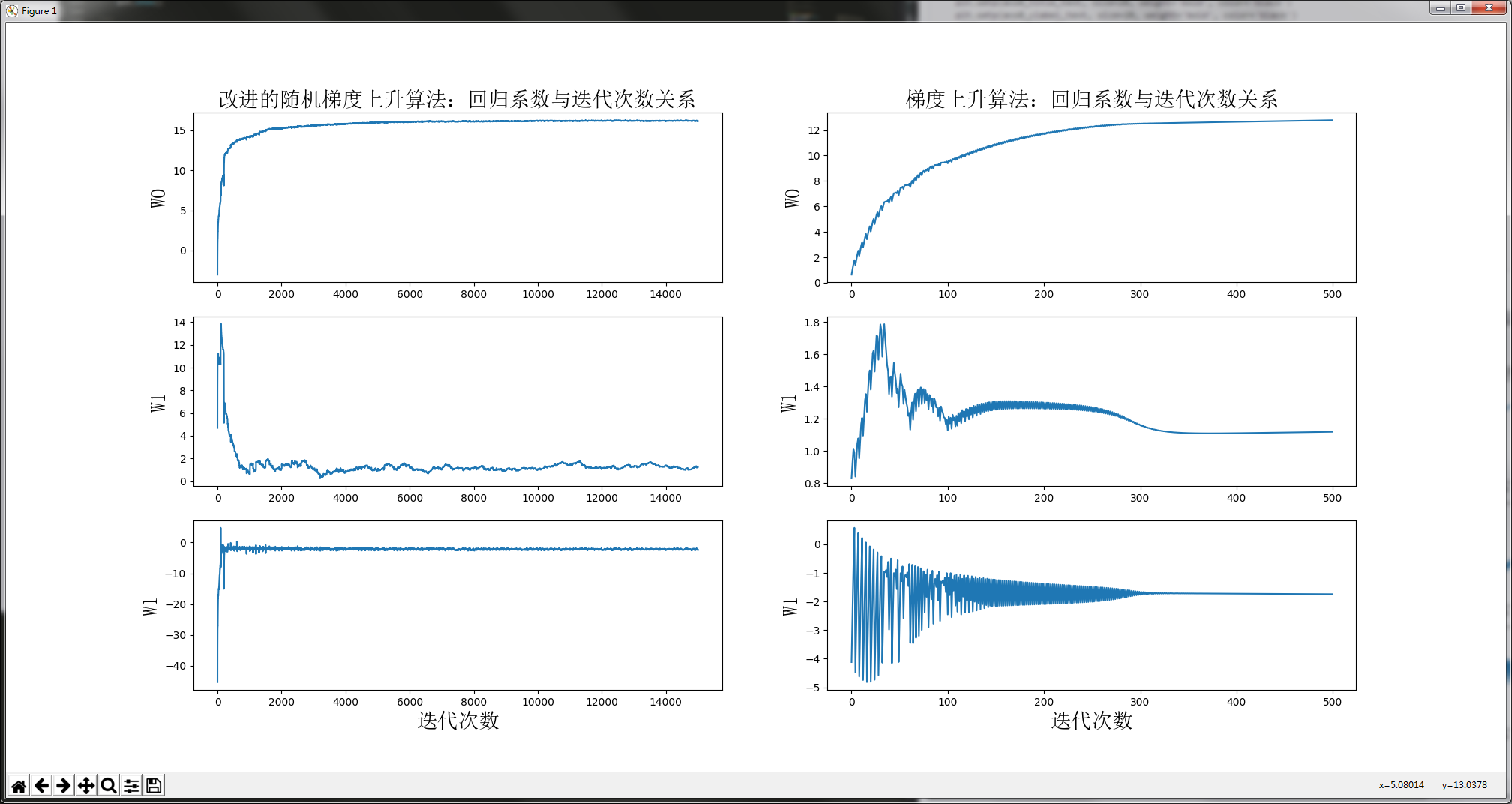

Because of the improved random gradient rising algorithm and random selection of sample points, the results of each run are different. But the general trend is the same. The convergence of our improved algorithm is better. Why do you say that? Let's analyze. We have 100 sample points in total, and the number of iterations of the improved algorithm is 150. The reason why the above figure shows 15000 iterations is that the regression coefficient is updated with one sample. Therefore, 150 iterations are equivalent to updating the regression coefficient 150 * 100 = 15000 times. In short, 150 iterations and 15000 regression parameters were updated. From the regression effect of the improved random gradient rise algorithm on the left side of the figure above, it can be seen that, in fact, when updating 2000 regression coefficients, it has converged. It is equivalent to traversing the whole dataset 20 times, the regression coefficient has converged. Training completed.

Let's take a look at the regression effect of the gradient rise algorithm on the right side of the figure above. Every time the gradient rise algorithm updates the regression coefficient, it needs to traverse the entire data set. It can be seen from the figure that the regression coefficient converges only when the number of iterations is more than 300. To make a whole, it converges when it traverses the whole dataset 300 times.

There is no harm without comparison. The improved random gradient algorithm starts to converge at the 20th time of traversing the dataset. But the gradient rise algorithm starts to converge at the 300th time of traversing the dataset. Imagine, with a lot of data, who is better?