Hanoi Tower problem is a common and classic problem solved by recursion.

What is the Hanoi Tower?

Hanoi Tower originated from the legend of ancient India and an ancient legend of India.

When the great Brahman created the world, he made three diamond pillars. On one pillar, 64 pieces of gold discs were stacked in order of size from the bottom to the top.

Brahman ordered Brahman to rearrange the disc on another pillar in order of size from below. At any time, the disk can not be enlarged on the small disk, and only one disk can be moved between three columns at a time.

Generally speaking, there are three columns A, B and C. begin to stack 64 plates on column A from top to bottom in the order of small to large. Put all plates on column A on column C in the order of small to large, and at any time, the disk cannot be enlarged on the small disk, and only one disk can be moved between the three columns at A time.

---------------------------------

Now take three plates to hold chestnuts!!!

Be careful:

Let's analyze:

First of all, we need to have a concept that when we start moving, we think of the bottom plate as a whole, and the rest of the top plate as a whole.

Realize A to C from the three plates in the figure below. First, consider the two plates above as A whole to enable them to reach B (original to step 1, note: since only one can be moved at A time, and the small ones are on the top, the two plates above first arrive at C and then arrive at B to realize the two plates above as A whole to B pillar). Then, let the largest plate go from A to C, and then let the plates on B as A whole realize all plates from B to A and then to C Move (internal move from step 2 to step 3).

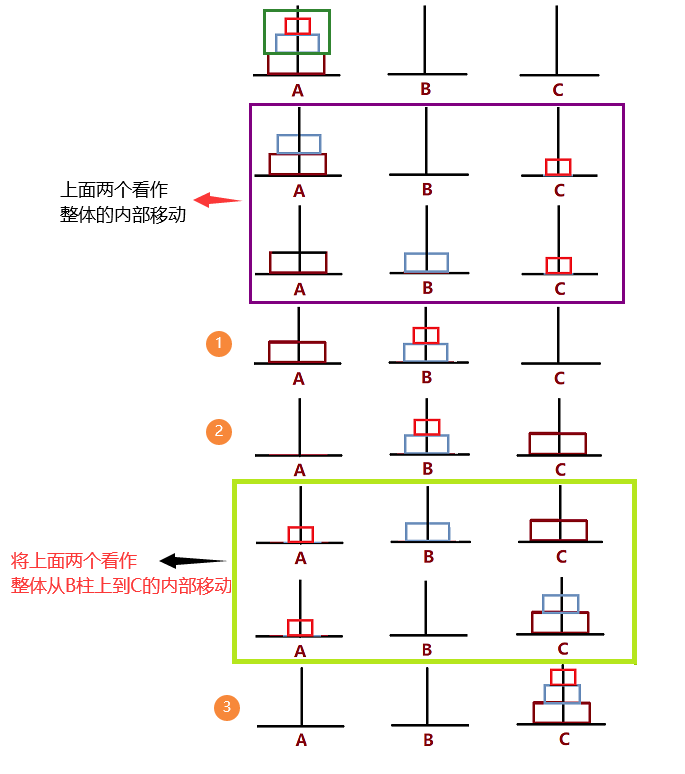
So according to the figure above, we can summarize the rules

When A column is placed on A plate, the movement rule is as follows:

A to C

When A column put two plates (two plates are simple, so there is no drawing, hee hee!) The movement rule is as follows:

A to B
A to C
B to C

When A column is placed with three plates, the movement rule is as follows:

A to B

{the above two are regarded as A whole, from the purple box above: the above two go through A to C and then C to B}

**A to C

{step 1 to step 2}

B to C

{the steps in the green box above go through B to A and then to C}**

By analogy, if there are four plates, the first step is to take the above three as A whole, let the above three go through A to C and then to B to realize the three as A whole to B,

After that: let the fourth largest plate go to C,

Then, let the three blocks above B go through some internal operations, from B to A and then to C.

----------

For the n-1 plate, first move the n-1 plate from A to B through some operations, then move the n-1 plate from B to C through some operations

----------—
Code diagram above!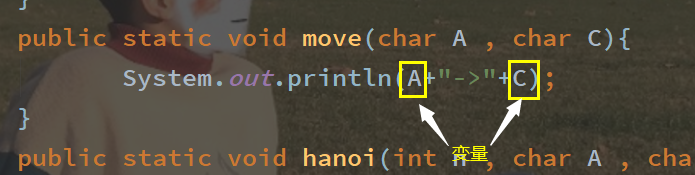

Code:

import java.util.Scanner;
public class hanoiTower {
    public static void main(String[] args) {
        System.out.println("Enter the number of plates to move:");
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        char A = 'A';
        char B = 'B';
        char C = 'C';
        System.out.println("The steps required are:");
        hanoi(n,A,B,C);
    }
    public static void move(char A , char C){
           System.out.println(A+"->"+C);
    }
    public static void hanoi(int n , char A , char B , char C){
        if (n==1){
            move(A , C);
        }else{
            hanoi(n-1 , A , C , B);
            move(A , C);
            hanoi(n-1 , B , A , C);
        }
    }
}

Test:

Frog jumps on the steps

A frog can jump up one or two steps at a time. Find out how many ways the frog can jump to an n-level step.

From the following figure, we can find the law. Starting from the third step, each step jumping method is equal to the sum of the first two steps jumping methods. eg: when the number of steps is 6, there are 5 + 8 = 13 ways for frogs to jump steps.

It can be compared with peibonaceh sequence: sum=f(n-1)+f(n-2)

Up code!!!

Recursion:

import java.util.Scanner;
public class frogSeat {
    public static void main(String[] args) {
        System.out.println("Enter the number of steps for the frog to jump:");
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int sum = jump(n);
        System.out.println("Frog has"+sum+"Seed jump method!");
    }
    public static int jump(int n){
        int sum = 0 ;
        if(n==1){
            return n ;
        }else if(n==2){
            return n ;
        }else{
            sum = jump(n-1)+jump(n-2);
        }
        return sum ;
    }
}
//Test:
//Enter the number of steps for the frog to jump:
10
//Frog has89Seed jump method!

Non recursive:

1. Using variables

import java.util.Scanner;
public class frogSeat {
        public static void main(String[] args) {
            System.out.println("Enter the number of steps for the frog to jump:");
            Scanner sc = new Scanner(System.in);
            int n = sc.nextInt();
            int sum = jump(n);
            System.out.println("Frog has"+sum+"Seed jump method!");
        }
        public  static int jump(int n){
            int i = 1 ;
            int j = 2 ;
            int k = 0 ;
            if (n==1){
                return n ;
            }else if(n==2) {
                return n ;
            } else{
                for (int a = 3 ; a<=n ; a++){
                    k = i+j ;
                    i=j;
                    j=k;
                }
                return k ;
            }
        }
    }
//Test:    
//Enter the number of steps for the frog to jump:
6
//Frog has13Seed jump method!

2. Using arrays

import java.util.Scanner;
public class frogSeat {
    public static void main(String[] args) {
        System.out.println("Enter the number of steps for the frog to jump:");
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        jump(n);
    }
        public  static void jump(int n) {
        int []funArrays = new int[999];
        funArrays[0] = 1;
        funArrays[1] = 2;
        int j = 0 ;
        if (n == 1) {
            System.out.println("Method has"+ funArrays[0]+"Kind!");
        }
        if (n == 2) {
            System.out.println("Method has"+ funArrays[1]+"Kind!");
        }else {
            for (j = 2; j <= n-1; j++) {
                funArrays[j]=funArrays[j-1]+funArrays[j-2];

            }
            System.out.println("Method has"+ funArrays[n-1]+"Kind!");
        }
     }
}