Catalogue
P34-4.7 overview of binary tree with sequential storage
P35-4.8 traversal of binary tree stored in sequence
P36-4.9 heap sorting of common sorting algorithms
P37-4.10 overview of cue binary tree
P38-4.11 implementation of cue binary tree code
P39-4.12 traversal of clue binary tree
P34-4.7 overview of binary tree with sequential storage
Binary tree and array conversion


In general, only the complete binary tree is considered!
The left child node of the nth element is: 2*n+1;
The right child node of the nth element is: 2*n+2;
The parent node of the nth element is: (n-1)/2;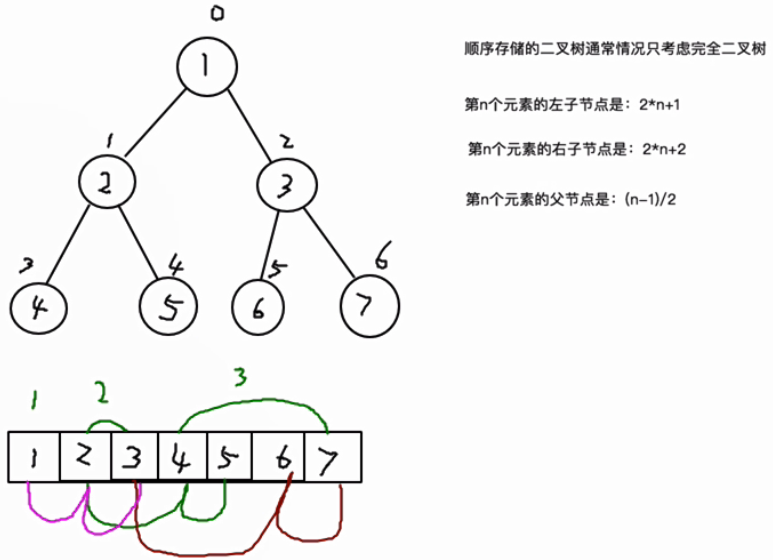
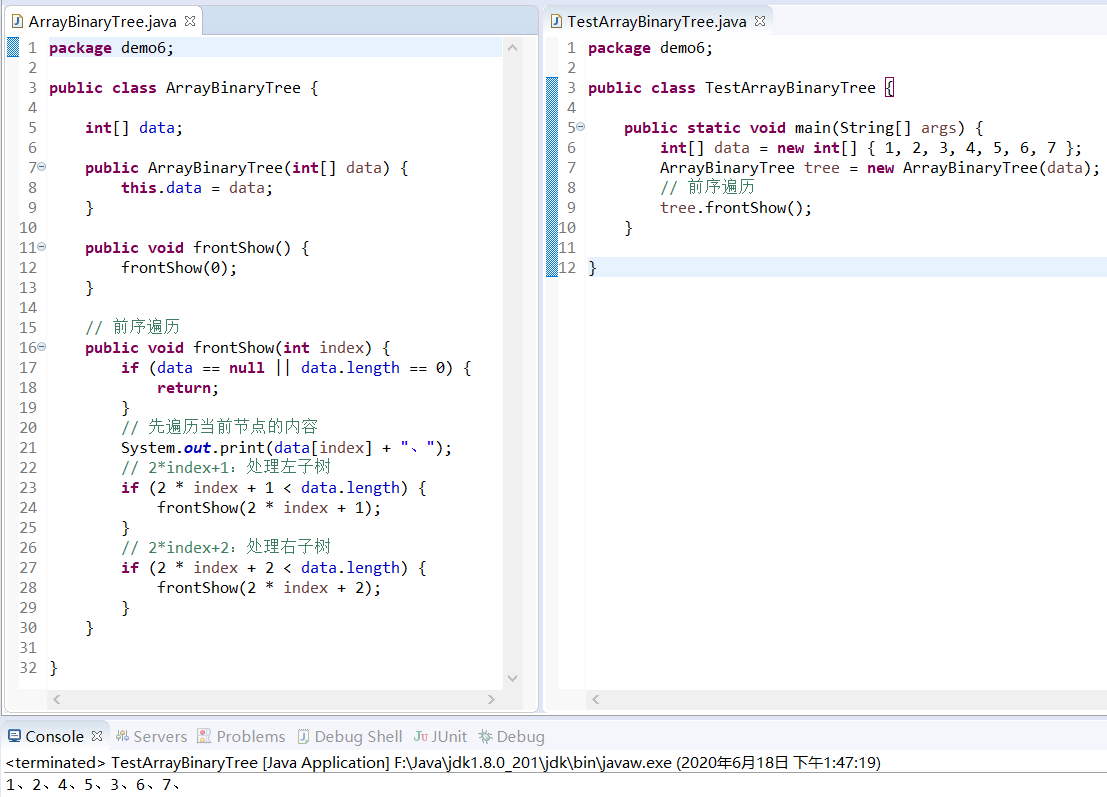
P35-4.8 traversal of binary tree stored in sequence
Think of the array as a complete binary tree! Traversing binary tree by array!
Because the left child of the root node also has a left child, recursion is required.
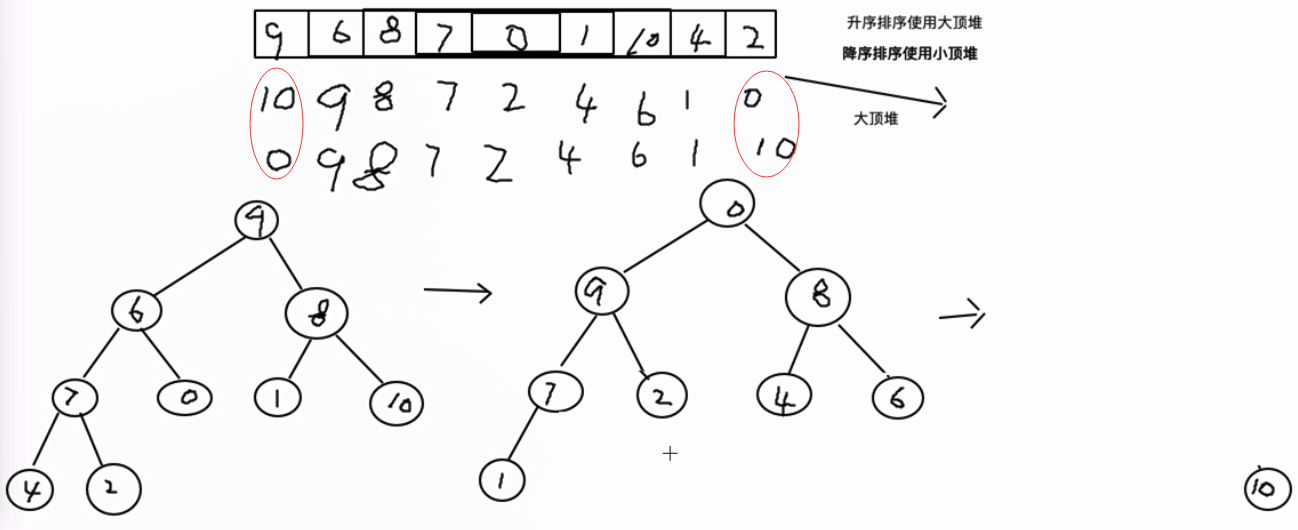
P36-4.9 heap sorting of common sorting algorithms
Big top heap: the parent node is always larger than the child node! The big one is above!
The big top pile is from big to small, and the small top pile is from small to large!
Ascending sort uses large top heap; descending sort uses small top heap.
package demo4;
import java.util.Arrays;
public class HeapSort {
public static void main(String[] args) {
int[] arr = new int[] { 9, 6, 8, 7, 0, 1, 10, 4, 2 };
heapSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void heapSort(int[] arr) {
// The start position is the last non leaf node, the parent of the last node
int start = (arr.length - 1) / 2;
// Adjust to large top reactor
for (int i = start; i >= 0; i--) {
maxHeap(arr, arr.length, i);
}
// First exchange the zeroth number in the array with the last number in the heap, and then treat the previous one as a large top heap
for (int i = arr.length - 1; i > 0; i--) {
int temp = arr[0];
arr[0] = arr[i];
arr[i] = temp;
maxHeap(arr, i, 0);
}
}
public static void maxHeap(int[] arr, int size, int index) {
// Left child node
int leftNode = 2 * index + 1;
// Right child node
int rightNode = 2 * index + 2;
int max = index;
// Compare with the two sub nodes to find the largest node
if (leftNode < size && arr[leftNode] > arr[max]) {
max = leftNode;
}
if (rightNode < size && arr[rightNode] > arr[max]) {
max = rightNode;
}
// change of position
if (max != index) {
int temp = arr[index];
arr[index] = arr[max];
arr[max] = temp;
// After swapping positions, the previously arranged heap may be destroyed. Therefore, the previously arranged heap needs to be readjusted
maxHeap(arr, size, max);
}
}
}P37-4.10 overview of cue binary tree
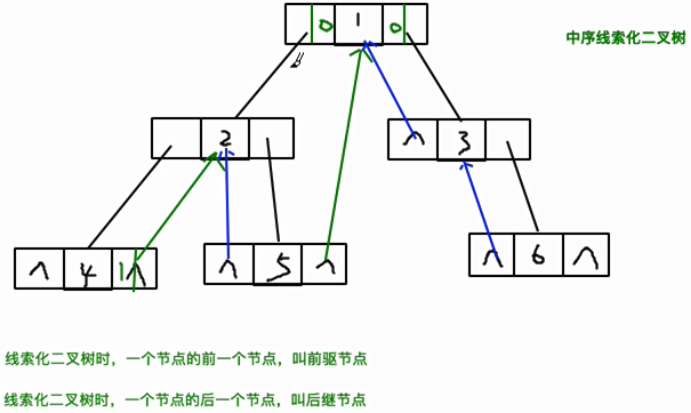
Left and right pointers. If nothing is stored, you can point the pointer of the node to the previous node or the next node of the node.

Find a marker to distinguish left (right subtree) and front (back node).
When a threaded binary tree is used, the previous node of a node is called the predecessor node;
When a threaded binary tree is used, the next node of a node is called the successor node.
P38-4.11 implementation of cue binary tree code
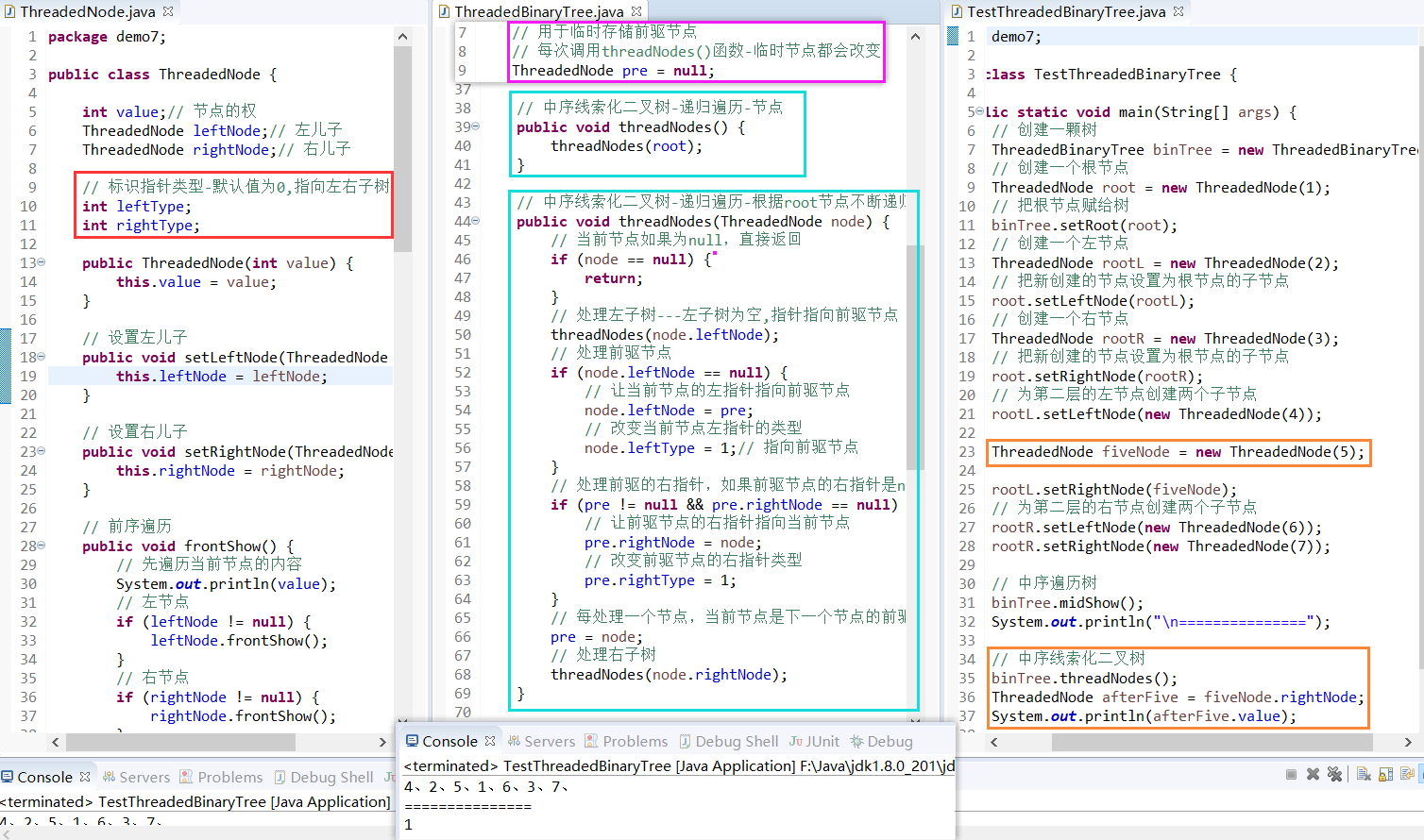
1,TestThreadedBinaryTree.java
package demo7;
public class TestThreadedBinaryTree {
public static void main(String[] args) {
// Create a tree
ThreadedBinaryTree binTree = new ThreadedBinaryTree();
// Create a root node
ThreadedNode root = new ThreadedNode(1);
// Assign root node to tree
binTree.setRoot(root);
// Create a left node
ThreadedNode rootL = new ThreadedNode(2);
// Set the newly created node as a child of the root node
root.setLeftNode(rootL);
// Create a right node
ThreadedNode rootR = new ThreadedNode(3);
// Set the newly created node as a child of the root node
root.setRightNode(rootR);
// Create two child nodes for the left node of the second layer
rootL.setLeftNode(new ThreadedNode(4));
ThreadedNode fiveNode = new ThreadedNode(5);
rootL.setRightNode(fiveNode);
// Create two child nodes for the right node of the second layer
rootR.setLeftNode(new ThreadedNode(6));
rootR.setRightNode(new ThreadedNode(7));
// Middle order ergodic tree
binTree.midShow();
System.out.println("\n===============");
// Middle order threaded binary tree
binTree.threadNodes();
ThreadedNode afterFive = fiveNode.rightNode;
System.out.println(afterFive.value);
}
}2,ThreadedBinaryTree.java
package demo7;
public class ThreadedBinaryTree {
ThreadedNode root;
// For temporary storage of the front drive node
// Every time the threadNodes() function is called - the temporary node changes
ThreadedNode pre = null;
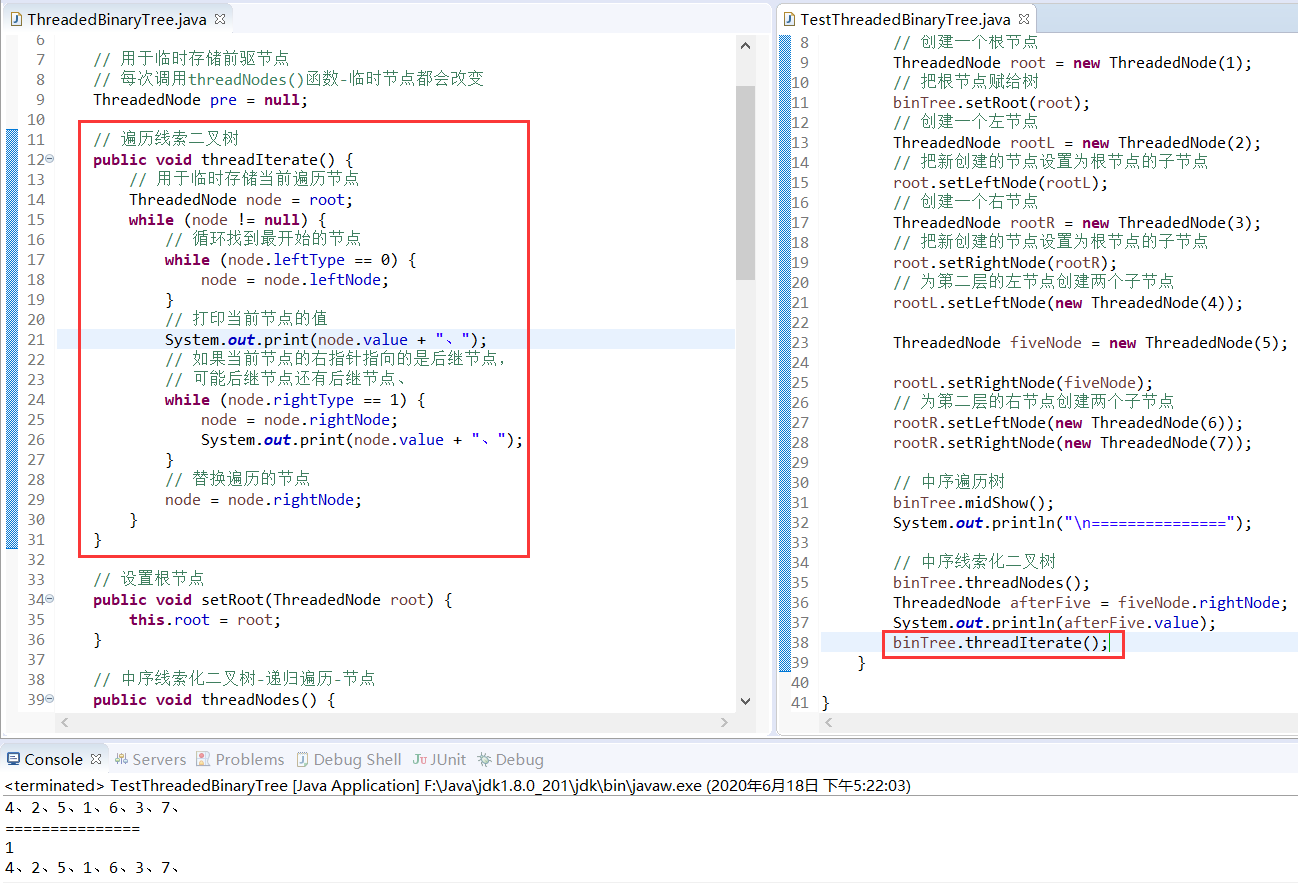
// Ergodic clue binary tree
public void threadIterate() {
// Used to temporarily store the current traversal node
ThreadedNode node = root;
while (node != null) {
// Loop to the beginning node
while (node.leftType == 0) {
node = node.leftNode;
}
// Print the value of the current node
System.out.println(node.value);
// If the right pointer of the current node points to a successor node,
// There may be subsequent nodes
while (node.rightType == 1) {
node = node.rightNode;
System.out.println(node.value);
}
// Replace traversed nodes
node = node.rightNode;
}
}
// Set root node
public void setRoot(ThreadedNode root) {
this.root = root;
}
// Middle order threaded binary tree recursive traversal node
public void threadNodes() {
threadNodes(root);
}
// Middle order threaded binary tree - recursive traversal - recursion according to root node
public void threadNodes(ThreadedNode node) {
// If the current node is null, return directly
if (node == null) {
return;
}
// Process left subtree - the left subtree is empty and the pointer points to the precursor node
threadNodes(node.leftNode);
// Processing precursor nodes
if (node.leftNode == null) {
// Let the left pointer of the current node point to the predecessor node
node.leftNode = pre;
// Change the left pointer type of the current node
node.leftType = 1;// Point to the precursor node
}
// Process the right pointer of the precursor. If the right pointer of the precursor node is null (no right subtree is pointed to)
if (pre != null && pre.rightNode == null) {
// Make the right pointer of the precursor node point to the current node
pre.rightNode = node;
// Change the right pointer type of the precursor node
pre.rightType = 1;
}
// For each node processed, the current node is the precursor node of the next node
pre = node;
// Process right subtree
threadNodes(node.rightNode);
}
// Get root node
public ThreadedNode getRoot() {
return root;
}
// Preorder ergodic
public void frontShow() {
if (root != null) {
root.frontShow();
}
}
// Middle order ergodic
public void midShow() {
if (root != null) {
root.midShow();
}
}
// Postorder ergodic
public void afterShow() {
if (root != null) {
root.afterShow();
}
}
// Preamble search
public ThreadedNode frontSearch(int i) {
return root.frontSearch(i);
}
// Delete subtree
public void delete(int i) {
if (root.value == i) {
root = null;
} else {
root.delete(i);
}
}
}3,ThreadedNode.java
package demo7;
public class ThreadedNode {
int value;// Weight of node
ThreadedNode leftNode;// Left son
ThreadedNode rightNode;// Right son
// Identity pointer type - default is 0, pointing to left and right subtrees
int leftType;
int rightType;
public ThreadedNode(int value) {
this.value = value;
}
// Set up the left son
public void setLeftNode(ThreadedNode leftNode) {
this.leftNode = leftNode;
}
// Set right son
public void setRightNode(ThreadedNode rightNode) {
this.rightNode = rightNode;
}
// Preorder ergodic
public void frontShow() {
// Traverse the content of the current node first
System.out.println(value);
// Left node
if (leftNode != null) {
leftNode.frontShow();
}
// Right node
if (rightNode != null) {
rightNode.frontShow();
}
}
// Middle order ergodic
public void midShow() {
// Left child node
if (leftNode != null) {
leftNode.midShow();
}
// Current node
System.out.print(value + ",");
// Right child node
if (rightNode != null) {
rightNode.midShow();
}
}
// Postorder traversal
public void afterShow() {
// Left child node
if (leftNode != null) {
leftNode.afterShow();
}
// Right child node
if (rightNode != null) {
rightNode.afterShow();
}
// Current node
System.out.println(value);
}
// Preamble search
public ThreadedNode frontSearch(int i) {
ThreadedNode target = null;
// Compare the value of the current node
if (this.value == i) {
return this;
// The value of the current node is not the node to find
} else {
// Find the left son
if (leftNode != null) {
// It may or may not be found. If not, target is still null
target = leftNode.frontSearch(i);
}
// If it is not empty, it means it has been found in the left son
if (target != null) {
return target;
}
// Find right son
if (rightNode != null) {
target = rightNode.frontSearch(i);
}
}
return target;
}
// Delete a subtree
public void delete(int i) {
ThreadedNode parent = this;
// Judge left son
if (parent.leftNode != null && parent.leftNode.value == i) {
parent.leftNode = null;
return;
}
// Judge right son
if (parent.rightNode != null && parent.rightNode.value == i) {
parent.rightNode = null;
return;
}
// Recursively check and delete left son
parent = leftNode;
if (parent != null) {
parent.delete(i);
}
// Recursively check and delete right son
parent = rightNode;
if (parent != null) {
parent.delete(i);
}
}
}P39-4.12 traversal of clue binary tree
No need to use recursion!!!