Question: find all prime numbers within 100

  This is a very basic and classic small code. It is very likely that we will traverse the filter in this way:

def find_odd(numb):
    flag = 0
    if numb ==2:
        return True
    else:
        for i in range(2,numb):
            flag = 0
            if numb%i == 0:
                return False
        flag = 1
    if flag == 1:
        return True
 
if __name__ == "__main__":
    my_list = []
    for i in range(2,101):
        if find_odd(i) ==True:
            my_list.append(i)
        else:
            continue
    print(my_list)

Fine, it has normally completed our set tasks, but now it needs to be faster? What if it's not within 100 but within a larger range?

Here we only need a little change to traverse from 2 to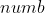Change from 2 to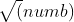This will save a lot of time when dealing with its wide range.

def find_odd(numb):
    flag = 0
    if numb ==2:
        return True
    else:
        j = int(round(numb**0.5)+1)
        for i in range(2,j):
            flag = 0
            if numb%i == 0:
                return False
        flag = 1
    if flag == 1:
        return True
 
if __name__ == "__main__":
    my_list = []
    for i in range(2,101):
        if find_odd(i) ==True:
            my_list.append(i)
        else:
            continue
    print(my_list)

How about a little faster?

Well, here's a conclusion: any prime number greater than or equal to 5 must be distributed near the multiple of six

Note that the inverse proposition of this conclusion is not True

It can be understood simply as follows: 2 * 2 = 4, 2 * 3 = 6, 2 * 2 * 2 = 8, the integer multiples of 2 and 3 must not be prime numbers. On the whole integer axis covered by their integer multiples, there may be gaps near the multiples of 2 * 3

In other words, we don't have to filter so many numbers from 1 to numb to judge at a time. We just need to judge near the multiple of six

def find_odd(numb):
    flag = 0
    if numb ==2:
        return True
    else:
        j = int(round(numb**0.5)+1)
        for i in range(2,j):
            flag = 0
            if numb%i == 0:
                return False
        flag = 1
    if flag == 1:
        return True
 
if __name__ == "__main__":
    my_list = [2,3]
    for i in range(1,100//6+1):
        if find_odd(i*6-1) ==True:
            my_list.append(i*6-1)
        if find_odd(i*6+1)==True:
            my_list.append(i*6+1)
    print(my_list)

Under these two optimizations, the normal code is already very fast, but what if it needs to be faster???

Here we will introduce the famous algorithm Euler sieve

def EulerSieve(n):
            filter, primers = [False for _ in range(n + 1)], []
            for i in range(2, n + 1):
                if not filter[i]:
                    primers.append(i)
                for prime in primers:
                    if i * prime > n:
                        break
                    filter[i * prime] = True
                    if i % prime == 0:
                        break
            return primers
if __name__ =="__main__":
    mylist = EulerSieve(100)
    print(mylist)

First, assign all filter s to False as our "sieve" and regenerate it into an empty list of primers to store the results

The judgment logic is that if the element filter[i] is False, the element I (i.e. prime number) is added to the primers

Then multiply each element by the current cyclic quantity i in the primers, and change the corresponding multiplied index value in the filter to True (that is, it is filtered out), because the integer multiple of the prime number must be a non prime number. In this way, we reduce a lot of computation.

So let's check the code. Will it really be much faster?

import timeit
import matplotlib.pyplot as plt
def compare():
    E_time=[]
    N_time=[]
    Step=[]
    for step in range(1000,20001,2000):
        def EulerSieve(n=step):
            filter, primers = [False for _ in range(n + 1)], []
            for i in range(2, n + 1):
                if not filter[i]:
                    primers.append(i)
                for prime in primers:
                    if i * prime > n:
                        break
                    filter[i * prime] = True
                    if i % prime == 0:
                        break
            return primers

        def find_odd(numb):
            flag = 0
            if numb ==2:
                return True
            else:
                j = int(round(numb**0.5)+1)
                for i in range(2,j):
                    flag = 0
                    if numb%i == 0:
                        return False
                flag = 1
            if flag == 1:
                return True

        def Normal_find(n=step):
            mylist = []
            for i in range(2,n+1):
                if find_odd(i) == True:
                    mylist.append(i)
            return mylist
        E_time.append(round(timeit.timeit(EulerSieve, number=100),4))
        N_time.append(round(timeit.timeit(Normal_find, number=100),4))
        Step.append(step)
    return E_time,N_time,Step
if __name__ =="__main__":
    Y1_list,Y2_list,X_list=compare()
    plt.plot(X_list,Y1_list,color = 'red',label='EulerSieve Method')
    plt.plot(X_list,Y2_list,color='green',linewidth=1.0,linestyle='--',label='Normal Method')
    plt.ylabel('time consuming/s',fontproperties = 'SimHei',fontsize = 12)
    plt.xlabel('Maximum prime range/Hundred times',fontproperties = 'SimHei',fontsize = 12)
    plt.title('Comparison of prime number screening time between Euler sieve and conventional algorithm',fontproperties = 'SimHei',fontsize = 15)
    plt.show()

Just put the results

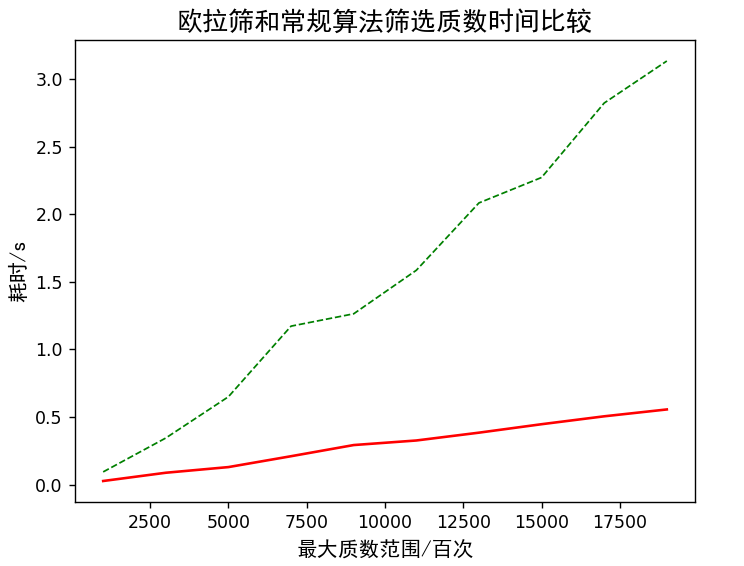
The green dotted line is the normal algorithm, and the red solid line is the Euler sieve algorithm, which is excellent with the naked eye