Binary tree

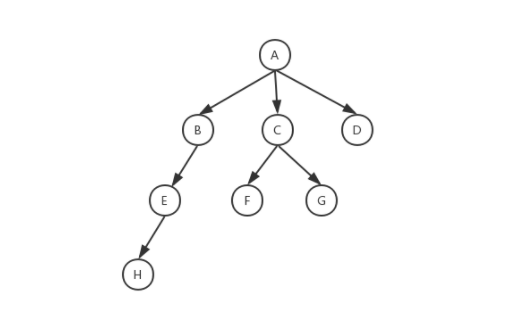
Tree: it is a nonlinear table structure with n (n > = 0) nodes. When n=0, it is called an empty tree. In any non empty tree:

• There is only one root node
• When n > 1, the other nodes can be divided into m (M > 0) disjoint finite sets T1,T2,..., Tm. Each set itself is a tree, which is called the subtree of the root
  

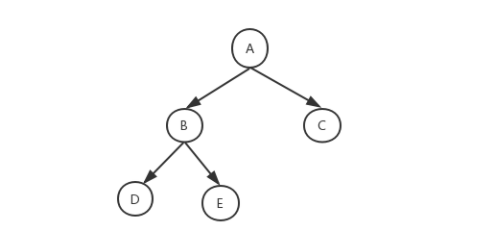
Binary tree: a tree in which each node has at most two child nodes. These two nodes are the left child node and the right child node respectively

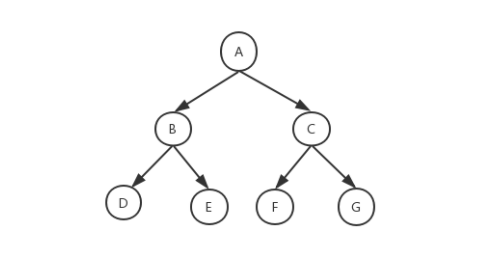
Full binary tree: there is a binary tree with all leaves at the bottom. Except for leaf nodes, each node has left and right child nodes

Complete binary tree: there is a binary tree. The leaf nodes are in the bottom two layers. The leaf nodes of the last layer are continuous from left to right, and there is no missing in the middle. Besides the last layer, the number of nodes in other layers should reach the maximum

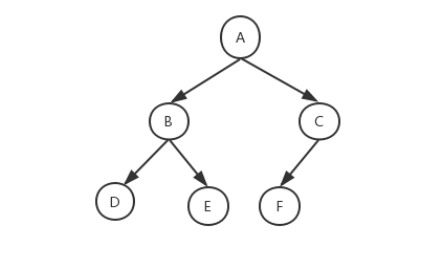
Properties of binary tree:

• Property 1: the maximum number of nodes on layer i of binary tree is 2{i-1} (i ≥ 1).
• Property 2: a binary tree with depth K has at most 2{k}-1 nodes (K ≥ 1).
• Property 3: the height of a binary tree containing N nodes is at least log2 (n+1).
• Property 4: in any binary tree, if the number of terminal nodes is n0 and the number of nodes with degree 2 is n2, then n0=n2+1.

Traversal of binary tree: no repeated access to each node in the binary tree (recursive idea)

• Preorder traversal: root left right
• Middle order traversal: left root right
• Post order traversal: left right root
• Breadth first traversal (hierarchical traversal): access layer by layer. After the node access of each layer is completed, access the next layer. No tree can be drawn through hierarchical traversal

Binary search tree: it is a kind of binary tree, but it only allows the left node to store smaller values (than the parent node) and the right node to store larger (or equal) values (than the parent node)

ES6 implements binary search tree:

class Node {
    constructor(val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}

class binarySearchTree {
    constructor() {
        this.root = null;
        this.result_array=[];
    }

    //Create a binary search tree, that is, the value of the root node is greater than that of the left node and less than that of the right node
    insertNodeByFather(node, newNode) {
        //If newnode < node value
        if (newNode.val < node.val) {
            //Judge whether the left node is empty
            if (node.left === null) {
                node.left = newNode;
            } else { //Continue to recursively find the next layer
                this.insertNodeByFather(node.left, newNode);
            }
        } else { //If newnode > node value
            if (node.right === null) {
                node.right = newNode;
            } else {
                this.insertNodeByFather(node.right, newNode);
            }
        }
    }
    insert(val) {
        //Create a new node
        let node = new Node(val);
        if (this.root === null) { //If there is no root node
            this.root = node;
        } else { //Otherwise, the insertNode method is called
            this.insertNodeByFather(this.root, node);
        }
    }
    //Preorder traversal: root right left
    preOrder(node) {
            if (node) {
                this.result_array.push(node.val);
                this.preOrder(node.left);
                this.preOrder(node.right);
            }
    }

    //Middle order traversal: left root right
    inOrder(node) {
            if (node) {
                this.inOrder(node.left);
                this.result_array.push(node.val);
                this.inOrder(node.right);
            }
    }

    //Postorder traversal: left and right roots
    postOrder(node) {
        if (node) {
            this.postOrder(node.left);
            this.postOrder(node.right);
            this.result_array.push(node.val);
        }
    }
    //Breadth first traversal (hierarchical traversal) starts from the first layer (root node) of the binary tree and traverses layer by layer from top to bottom; In the same layer, the nodes are accessed one by one from left to right
    levelOrderTraversal(node) {
        if (!node) {
            throw new Error('Empty Tree');
        }
        let que = [];
        que.push(node)
        while (que.length !== 0) {
            node = que.shift()
            this.result_array.push(node.val)
            if (node.left) que.push(node.left)
            if (node.right) que.push(node.right)
        }
    }
    //Clear the value of the stored tree node
    init(){
        this.result_array=[];
    }

    //Search minimum
    minNode(node){
        if (!node) return null;
        while (node.left){
            node=node.left;
        }
        return node.val;
    }

    //Search maximum
    maxNode(node){
        if (!node) return null;
        while (node.right){
            node=node.right;
        }
        return node.val;
    }
}

Test code:

let tree = new binarySearchTree();
let arr = [11,7,15,5,9,4,6,8,10];
arr.forEach((a) => {
    tree.insert(a);
});

let pre_arr = []; //Store preorder traversal sequence
let in_arr = []; //Storing middle order traversal sequence
let post_arr = []; //Store post order traversal sequence
let level_arr = []; //Store hierarchical traversal sequence

tree.preOrder(tree.root);
pre_arr=tree.result_array;
console.log('Preorder traversal:',pre_arr);

tree.init();//Clear the values in the array
tree.inOrder(tree.root);
in_arr=tree.result_array;
console.log('Middle order traversal:',in_arr);

tree.init();
tree.postOrder(tree.root);
post_arr=tree.result_array;
console.log('Post order traversal:',post_arr);

tree.init();
tree.levelOrderTraversal(tree.root);
level_arr=tree.result_array;
console.log('Hierarchy traversal:',level_arr);

console.log('Minimum:',tree.minNode(tree.root));
console.log('Maximum:',tree.maxNode(tree.root));

Output results:

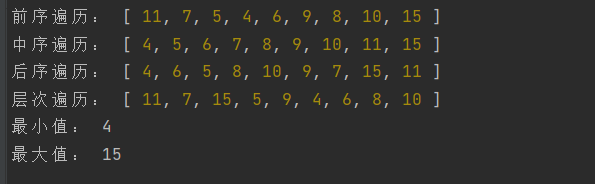
Case: input the array results of the preorder and inorder traversal of the binary tree to determine the binary tree structure

 class binaryTree {
    constructor(v, l, r) {
        this.val = v;
        this.left = l;
        this.right = r
    }
}

/**
 * Enter the results of preorder traversal and inorder traversal of a binary tree, please rebuild the binary tree.
 * It is assumed that the input pre order traversal and middle order traversal results do not contain duplicate numbers.
 * For example, enter the preorder traversal sequence {1,2,4,7,3,5,6,8} and the middle order traversal column {4,7,2,1,5,3,8,6},
 * Rebuild the binary tree and return.
 * 
 *   Input: previous order: [1,2,3,4,5,6,7], middle order: [3,2,4,1,6,5,7]   
     Output: tree structure
 */

function reConstructBinaryTree(pre, next) {
    // Recursive exit
    if (pre.length == 0 || next.length == 0 || pre.length != next.length) {
        return null;
    }
    // Get the root node
    let root = new binaryTree(pre[0]);
    // The position of the root node found in the middle order traversal
    let i = 0;
    while (next[i] != root.val) {
        i++;
    }
    //Determine the pre order traversal length of the left subtree
    let preLeft = new Array(i);
    //Determine the length of order traversal in the left subtree
    let inLeft = new Array(i);

    //Determine the preorder traversal length of the right subtree
    let preRight = new Array(next.length - i - 1);
    //Determine the order traversal length in the right subtree
    let inRight = new Array(next.length - i - 1);

    // Traversal gets the value of the middle order traversal before the left and right subtrees in turn
    for (let j = 0; j < next.length; j++) {
        if (j < i) {
            preLeft[j] = pre[j + 1];  //Start with j+1
            inLeft[j] = next[j];      //Start with j
        } else if (j > i) {
            preRight[j - i - 1] = pre[j];
            inRight[j - i - 1] = next[j];
        }
    }
    // recursion
    root.left = reConstructBinaryTree(preLeft, inLeft);
    root.right = reConstructBinaryTree(preRight, inRight);
    return root;
}

Test: determine the structure of the tree with known preorder and inorder

let pre = [1, 2, 3, 4, 5, 6, 7];
let next = [3, 2, 4, 1, 6, 5, 7];
let root = reConstructBinaryTree(pre, next);
console.log(root);

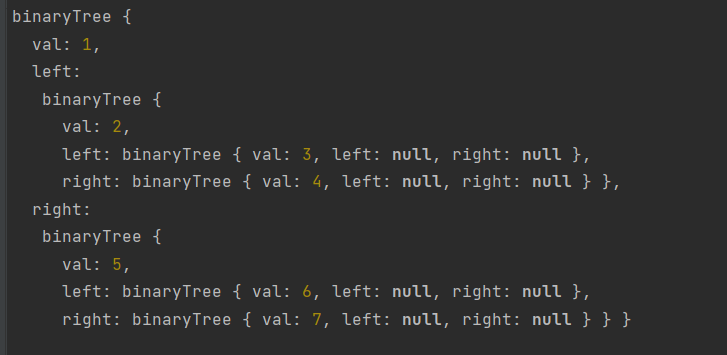
Structure of binary tree: