Count class dp
Given the scheme limit, count the number of occurrences of a certain scheme
Original question link
https://www.acwing.com/problem/content/902/
General idea of the topic
A positive integer n can be expressed as the sum of several positive integers, such as: n=n1+n2 +... + nk, where n1 ≥ n2 ≥... ≥ nk,k ≥ 1.
We call such a representation a partition of positive integer n. Now give a positive integer n
, please find out how many different partition methods there are for n.
0<n<=1000
thinking
Completely solved by backpacking.
f
(
i
,
j
)
f(i,j)
f(i,j) indicates front
i
i
i. put the number into the capacity of
j
j
Number of combinations of j's backpacks. Due to use
[
1
−
(
j
−
1
)
]
[1-(j-1)]
[1 − (j − 1)]
j
j
j. So we can fill it up.
Plain version:
Status indication:
f
(
i
,
j
)
f(i,j)
f(i,j) represents the number of j rounded up with a number from 1 to i
Status calculation:
f
(
i
,
j
)
=
f
(
i
−
1
,
j
)
+
f
(
i
−
1
,
j
−
1
∗
i
)
+
f
(
i
−
1
,
j
−
2
∗
i
)
+
.
.
.
f(i,j)=f(i-1,j)+f(i-1,j-1*i)+f(i-1,j-2*i)+...
f(i,j)=f(i−1,j)+f(i−1,j−1∗i)+f(i−1,j−2∗i)+...
Optimized version:
State representation: the same as the plain version, but the rolling array optimization is used
Status calculation:
f
(
j
)
=
f
(
j
)
+
f
(
j
−
i
)
f(j)=f(j)+f(j-i)
f(j)=f(j)+f(j−i)
See this blog for specific proof.
https://blog.csdn.net/qq_45931661/article/details/119999547
Other editions
Status indication:
f
(
i
,
j
)
f(i,j)
f(i,j) is represented by
j
j
j number rounding
i
i
Quantity of i
Status meter:
f
(
i
,
j
)
=
f
(
i
−
1
,
j
−
1
)
+
f
(
i
−
j
,
j
)
f(i,j)=f(i-1,j-1)+f(i-j,j)
f(i,j)=f(i−1,j−1)+f(i−j,j)
code
Simple version, complexity of O(n^3)
#include<iostream>
using namespace std;
const int N = 1005,mod = 1e9+7;
int n;
int f[N][N];
int main(){
cin>>n;
for(int i=0;i<=n;i++) f[i][0]=1;
for(int i=1;i<=n;i++){//Enumerate items
for(int j=1;j<=n;j++){//Enumerate Backpack Capacity
for(int k=0;k*i<=j;k++){//State calculation
f[i][j]=(f[i][j]+f[i-1][j-k*i])%mod;
}
}
}
cout<<f[n][n]<<endl;
return 0;
}
Optimized version, complexity of O(n^2).
#include<iostream>
using namespace std;
const int N = 1005,mod = 1e9+7;
int n;
int f[N];
int main(){
cin>>n;
f[0]=1;
for(int i=1;i<=n;i++){
for(int j=i;j<=n;j++){//Rolling state calculation
f[j]=(f[j]+f[j-i])%mod;
}
}
cout<<f[n]<<endl;
return 0;
}
Other editions:
#include<iostream>
using namespace std;
const int N = 1005,mod = 1e9+7;
int n;
int f[N][N];
int main(){
cin>>n;
f[0][0]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=i;j++){//State calculation
f[i][j]=(f[i-1][j-1]+f[i-j][j])%mod;
}
}
int res = 0 ;
for(int i=1;i<=n;i++){//Find the total quantity
res=(res+f[n][i])%mod;
}
cout<<res<<endl;
return 0;
}
Digital statistics DP
Some laws in statistics, such as the number of numbers and so on.
Title Link:
https://www.acwing.com/problem/content/340/
Main idea of the title:
Given two integers a and b, find the number of occurrences of 0 ∼ 9 in all numbers between a and b.
For example, if a=1024 and b=1032, there are 9 numbers between a and b as follows:
1024 1025 1026 1027 1028 1029 1030 1031 1032
Among them, 0 appears 10 times, 1 appears 10 times, 2 appears 7 times, 3 appears 3 times, and so on
Idea:
The idea of prefix sum can be used to find the number of occurrences of x in the interval [a,b],
r
e
s
=
c
o
u
n
t
(
b
,
x
)
−
c
o
u
n
t
(
a
−
1
,
x
)
res=count(b,x)-count(a-1,x)
res=count(b,x)−count(a−1,x)
Now analyze how to solve it
c
o
u
n
t
(
a
,
x
)
count(a,x)
count(a,x), that is, the number of times x appears in [1, a].
Set the required number as abcdefg
Take the case of x in position 4 as an example:
- x!=0
1. Form: { 0 − ( a b c − 1 ) } d { 0 − 1000 } \{0 - (abc-1)\}d\{0-1000\} {0−(abc−1)}d{0−1000}
Meaning: the prefix is less than abc
2.1. Form: a b c d { 0 − 1000 } abcd\{0-1000\} abcd{0−1000}
Meaning: d==x
2.2 form: a b c d { 0 − e f g } abcd\{0-efg\} abcd{0−efg}
Significance: d < x
2.3 form: does not exist
Meaning: d > x - x==0
1. Form: { 1 − ( a b c − 1 ) } d { 0 − 1000 } \{1 - (abc-1)\}d\{0-1000\} {1−(abc−1)}d{0−1000}
Meaning: if the prefix is less than abc, note that the prefix of 0 cannot be 0, otherwise it will be meaningless.
2.1. Form: a b c d { 0 − 1000 } abcd\{0-1000\} abcd{0−1000}
Meaning: d==x
2.2 form: a b c d { 0 − e f g } abcd\{0-efg\} abcd{0−efg}
Significance: d < x
2.3 form: does not exist
Meaning: d > x
Enumerating the number of times x appears on each bit can get the final answer.
code:
#include<iostream>
#include<vector>
#include<cmath>
using namespace std;
int n,m;
int get(vector<int > num, int r, int l){
//Biting r to l of num into a number
int res=0;
for(int i=r;i>=l;i--){
res=res*10+num[i];
}
return res;
}
int count(int a,int x){
//Count the times of x in 1~a
if(a==0) return 0;
vector<int > num;//Store every bit
while(a){
//Lower the standard and lower it
num.push_back(a%10);
a/=10;
}
int n = num.size();
long long res=0;
for(int i=n-1-!x;i>=0;i--){
//Enumerate each bit from high to low
res+=(long long )get(num,n-1,i+1)*pow(10,i);//1 Situation
if(!x) res-=pow(10,i);
if(x==num[i]) res+=get(num,i-1,0)+1;//2.1 situation
else if(x<num[i]) res+=pow(10,i);//2.2 situation
}
return res;
}
int main(){
while(cin>>n>>m,n||m){
if(n>m) swap(n,m);
for(int i=0;i<10;i++){
cout<<count(m,i)-count(n-1,i)<<" ";//Using the idea of prefix and
}
cout<<endl;
}
return 0;
}
State compression DP
The process of realizing dp by representing the state in binary bits.
Mondrian's dream
Original title link:
https://www.acwing.com/problem/content/293/
Main idea of the title:
Please put N × The chessboard of M is divided into several 1 × How many schemes are there for the rectangle of 2.
For example, when N=2 and M=4, there are five schemes. When N=2 and M=3, there are three schemes.
As shown in the figure below:

Idea:
1. It can be found that once the position of the horizontal building block is given, the position of the vertical building block is also determined.
2. Use the binary of j to represent the state of each column. As shown in the figure below, the status of column i is
(
100
)
2
(100)_2
(100)2
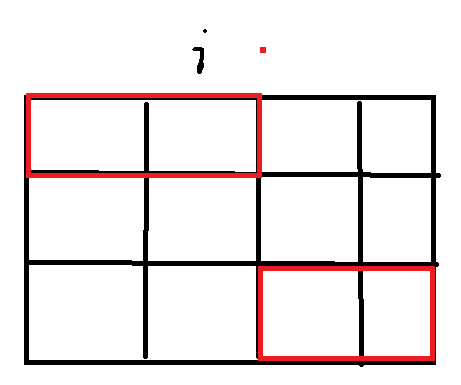
**Status indication:
f
(
i
,
j
)
f(i,j)
f(i,j) represents the second
i
i
Column i, status
j
j
Number of filling schemes for j.

Status calculation: f ( i , j ) + = f ( i − 1 , k ) f(i,j)+=f(i-1,k) f(i,j)+=f(i − 1,k), but this recurrence has two requirements**
1.
(
j
&
k
)
=
=
0
( j\& k)==0
(j&k)==0
Because it is assumed that a horizontal building block is filled to the left in the binary 1 bit of k. If one of j and k is 1 at the same time, a conflict will occur.
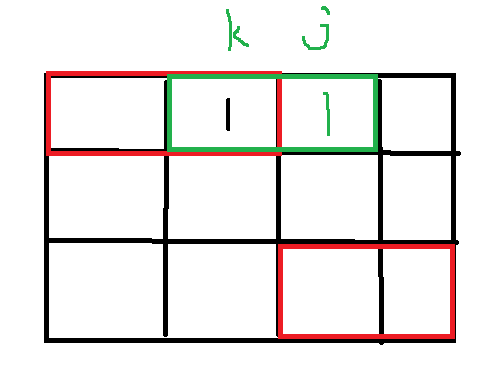
2.
(
j
∣
k
)
(j|k)
(j ∣ k) there are no consecutive odd zeros
If there are consecutive odd zeros, and 0 means no horizontal building blocks. Then this position is filled only with vertical blocks, and the vertical blocks cannot complete the filling of odd height. So there will be a vacancy, which will be rounded off here.
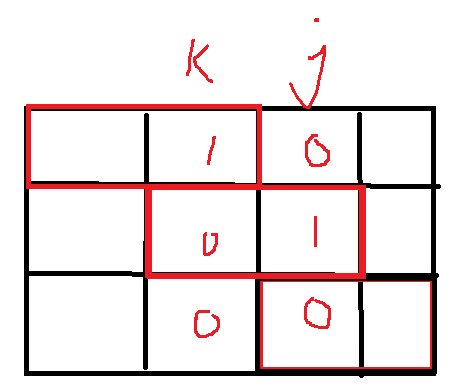
code
Don't write shift left operation as shift right operation like me...
#include<iostream>
#include<cstring>
using namespace std;
const int N = 1<<12;
int n,m;
long long f[15][N];
bool st[N];
int main(){
while(cin>>n>>m, n||m){
memset(f,0,sizeof f);
//Pretreatment
for(int i = 0; i < 1<<n; i++){
//i stands for status
int cnt = 0;//Number of consecutive 0 stored
st[i] = true;
for(int j = 0; j < n;j++){
//Enumerate each bit of the state to determine whether there are consecutive odd zeros
if(i>>j&1){
if(cnt&1) st[i] = false;
cnt = 0;
}else cnt++;
}
if(cnt&1) st[i]=false;//Judge the last consecutive 0
}
f[0][0]=1;
for(int i=1;i<=m;i++){
//Enumeration column
for(int j=0;j<1<<n;j++){
for(int k=0;k<(1<<n);k++){
if((j&k) == 0 && st[j|k]){
f[i][j]+=f[i-1][k];
}
}
}
}
cout<<f[m][0]<<endl;
}
return 0;
}
Shortest Hamilton ian path
Original title link:
https://www.acwing.com/problem/content/93/
General idea of the topic
Given a weighted undirected graph with n points labeled from 0 ∼ n − 1, find the shortest Hamilton path from starting point 0 to ending point n − 1.
Hamilton path is defined as passing through each point exactly once from 0 to n − 1.
thinking
Status indication:
f
(
i
,
j
)
f(i,j)
f(i,j) represents the situation of starting from 0 to j and passing through i. i is represented in binary. For example, 1001 represents the path through node 0 and node 3.
State transition:
f
(
i
,
j
)
=
m
i
n
(
f
[
t
]
[
k
]
+
w
[
k
]
[
j
]
)
,
t
surface
show
through
too
i
of
front
one
individual
shape
state
,
k
surface
show
When
front
stay
t
shape
state
of
which
individual
section
spot
upper
.
f(i,j)=min(f[t][k]+w[k][j]),t represents the previous state after i, and K represents which node is currently in T state.
f(i,j)=min(f[t][k]+w[k][j]),t represents the previous state after i, and K represents which node is currently in T state.
code
#include<iostream>
#include<cstring>
using namespace std;
const int N = 25;
int f[1<<20][N];
int w[N][N];
int main(){
int n;
cin>>n;
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
cin>>w[i][j];
}
}
memset(f,0x3f,sizeof f);
f[1][0]=0;
for(int i=1;i<1<<n;i++){//state
for(int j=0;j<n;j++){//node
if(( i>>j ) & 1){
int t = i-(1<<j);//Backtracking may be transferred to the state of i
for(int k=0;k<n;k++){
if(t>>k & 1){//Determine the current node
f[i][j] = min(f[t][k]+w[k][j],f[i][j]);
}
}
}
}
}
cout<<f[(1<<n)-1][n-1]<<endl;
return 0;
}
Tree dp
Original title link:
https://www.acwing.com/problem/content/287/
General idea of the topic
Ural university has N employees, numbered 1 ∼ N.
Their relationship is like a tree with the principal as the root, and the parent node is the direct boss of the child node.
Each employee has a happiness index, which is given by the integer Hi, where 1 ≤ i ≤ N.
Now we are going to hold an anniversary party, but no staff is willing to attend the meeting with their direct supervisor.
On the premise of meeting this condition, the organizer hopes to invite some staff to the meeting to maximize the total happiness index of all staff participating in the meeting.
thinking
Status indication:
f
(
i
,
j
)
,
j
∈
{
0
,
1
}
f(i,j),j∈\{0,1\}
f(i,j),j ∈ {0,1} represents the maximum value of the subtree with I as the root node, j=0 represents not taking node i, and j=1 represents taking node I.
Status calculation:
f
(
i
,
0
)
=
s
u
m
(
m
a
x
(
f
(
k
1
,
0
)
,
f
(
k
1
,
1
)
)
,
m
a
x
(
f
(
k
2
,
0
)
,
f
(
k
2
,
1
)
)
.
.
.
m
a
x
(
f
(
k
n
,
0
)
,
f
(
k
n
,
1
)
)
)
,
k
f(i,0)=sum(max(f(k_1,0),f(k_1,1)),max(f(k_2,0),f(k_2,1))...max(f(k_n,0),f(k_n,1))),k
f(i,0)=sum(max(f(k1, 0),f(k1, 1)),max(f(k2, 0),f(k2, 1))...max(f(kn, 0),f(kn, 1))), k represents the child node of i.
f
(
i
,
1
)
=
s
u
m
(
f
(
k
1
,
0
)
,
f
(
k
2
,
0
)
.
.
.
f
(
k
n
,
0
)
)
f(i,1)=sum(f(k_1,0),f(k_2,0)...f(k_n,0))
f(i,1)=sum(f(k1,0),f(k2,0)...f(kn,0))
code
#include<iostream>
#include<cstring>
using namespace std;
const int N = 6005;
int f[N][2];
int H[N],has_head[N];
int h[N],e[N],ne[N],ind;
void add(int a,int b){
//Add b to a
e[ind]=b,ne[ind]=h[a],h[a]=ind++;
}
void dfs(int root){
//dfs for dp
for(int i=h[root];i!=-1;i=ne[i]){
int t = e[i];
dfs(t);
f[root][0] += max(f[t][0],f[t][1]);
f[root][1] += f[t][0];
}
f[root][1] += H[root];
}
int main(){
memset(h,-1,sizeof h);
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>H[i];
}
for(int i = 0; i < n-1; i++){
int a,b;
cin>>a>>b;
has_head[a] = true;
add(b, a);//Building adjacency tables
}
int root=1;
while(has_head[root]) root++;//Find root node
dfs(root);
cout<<max(f[root][0],f[root][1])<<endl;
return 0;
}
Memory search
Original title link:
https://www.acwing.com/problem/content/903/
Main idea of the title:
Given a matrix of R rows and C columns, it represents a rectangular grid ski resort. The point in row i and column j of the matrix represents the height of the area in row i and column j of the ski resort.
Starting from an area in the ski resort, a person can slide up, down, left and right one unit distance at a time.
Of course, the premise that a person can slide to an adjacent area is that the height of the area is lower than the height of his current area.
Outputs an integer representing the longest ski length that can be completed.
Idea:
Status indication:
s
o
l
v
e
(
i
,
j
)
solve(i,j)
solve(i,j) indicates from
(
i
,
j
)
(i,j)
(i,j) the longest ski length of departure.
Status calculation:
s
o
l
v
e
(
x
,
y
)
=
m
a
x
(
s
o
l
v
e
(
x
−
1
,
y
)
,
s
o
l
v
e
(
x
,
+
1
,
y
)
,
s
o
l
v
e
(
x
,
y
−
1
)
,
s
o
l
v
e
(
x
,
y
+
1
)
)
+
1
solve(x,y)=max(solve(x-1,y),solve(x,+1,y),solve(x,y-1),solve(x,y+1))+1
solve(x,y)=max(solve(x−1,y),solve(x,+1,y),solve(x,y−1),solve(x,y+1))+1
Each solve(x,y) can be memorized to reduce the number of recursions.
code:
#include<iostream>
using namespace std;
const int N = 300+5;
int r,c;
int dp[N][N],a[N][N];
int dx[] = {0,1,0,-1},dy[] = {1,0,-1,0};
int solve(int i, int j){
if(dp[i][j]!=0) return dp[i][j];
int ans=1;
for(int k = 0; k < 4; k++){
int x=i+dx[k],y=j+dy[k];//Traverse four directions
if(x>=1 && x<=r && y>=1 && y<=c && a[x][y]<a[i][j]){
ans = max(solve(x,y)+1,ans);
}
}
dp[i][j]=ans;//memory
return ans;
}
int main(){
cin>>r>>c;
for(int i = 1; i <= r; i++){
for(int j = 1; j <= c; j++){
scanf("%d",&a[i][j]);
}
}
int res=0;
for(int i = 1; i <= r; i++){
for(int j = 1; j <= c; j++){
res = max(res,solve(i, j));//Find global maximum
}
}
cout<<res<<endl;
return 0;
}