1. Introduction to Algorithms
Archimedes optimization algorithm: a new metaheuristic algorithm for solving optimization problems
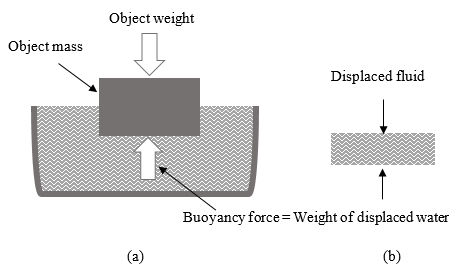
The difficulty and complexity of numerical optimization problems are increasing in the real world, which requires effective optimization methods. To date, various metaheuristic methods have been introduced, but only a few have been recognized in the research community. This paper presents a new metaheuristic algorithm, called Archimedean optimization algorithm (AOA).Solve optimization problems. AOA is inspired by interesting Archimedean laws of physics. It mimics the principle of buoyancy acting upward on an object partially or completely immersed in a fluid, proportional to the weight of the displaced fluid. To assess performance, the proposed AOA algorithm was tested on the CEC'17 test suite and four engineering design issues.Solutions perform better than the latest known technologies, and metaheuristic algorithms such as genetic algorithm (GA), particle swarm optimization (PSO), differential evolution variants L-SHADE and LSHADE-EpSin, whale optimization algorithm (WOA), sine-cosine algorithm (SCA), Harrishock optimization (HHO), and balance optimizer (EO) have recently been introduced.The experimental results show that AOA is a high performance optimization tool in terms of convergence rate and balance between exploration and development because it can effectively solve complex problems. The source code can now be made public to the public from the following locations: Whale Optimization Algorithm (WOA), Sine-Cosine Algorithm (SCA), Harris Eagle Optimization (HHO), and Balance Optimizer (EO)The experimental results show that AOA is a high performance optimization tool in terms of convergence rate and balance between exploration and development because it can effectively solve complex problems. The source code can now be made public to the public from the following locations: Whale Optimization Algorithm (WOA), Sine-Cosine Algorithm (SCA), Harris Eagle Optimization (HHO), and Balance Optimizer (EO)The experimental results show that AOA is a high performance optimization tool in terms of convergence rate and balance between exploration and development, because it can effectively solve complex problems.
2. Partial Codes
%_______________________________________________________________________________________
% The Arithmetic Optimization Algorithm (AOA) source codes demo version 1.0
%
% Developed in MATLAB R2015a (7.13)
%
% Main paper: The Arithmetic Optimization Algorithm
% Reference: Abualigah, L., Diabat, A., Mirjalili, S., Abd Elaziz, M., and Gandomi, A. H. (2021). The Arithmetic Optimization Algorithm. Computer Methods in Applied Mechanics and Engineering.
%
%_______________________________________________________________________________________
clear all
clc
Solution_no=20; %Number of search solutions
F_name='F1'; %Name of the test function F1-f23
M_Iter=1000; %Maximum number of iterations
[LB,UB,Dim,F_obj]=Get_F(F_name); %Give details of the underlying benchmark function
[Best_FF,Best_P,Conv_curve]=AOA(Solution_no,M_Iter,LB,UB,Dim,F_obj); % Call the AOA
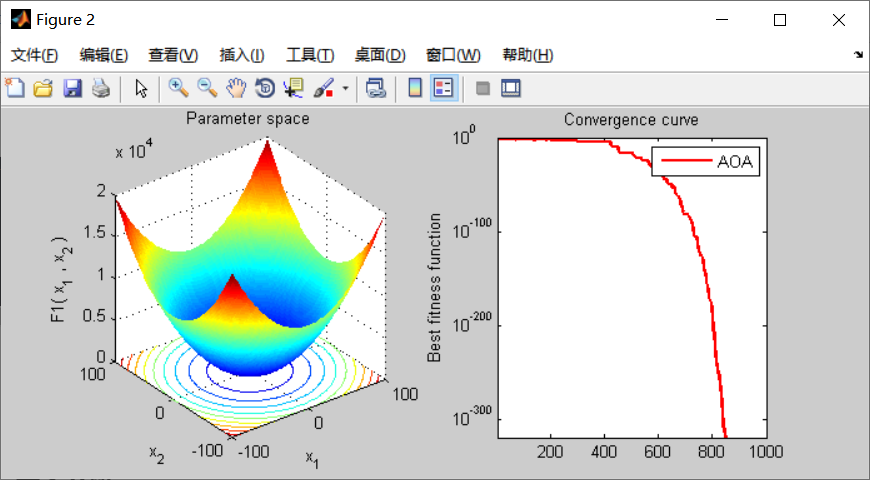
figure('Position',[454 445 694 297]);
subplot(1,2,1);
func_plot(F_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([F_name,'( x_1 , x_2 )'])
subplot(1,2,2);
semilogy(Conv_curve,'Color','r','LineWidth',2)
title('Convergence curve')
xlabel('Iteration#');
ylabel('Best fitness function');
axis tight
legend('AOA')
display(['The best-obtained solution by Math Optimizer is : ', num2str(Best_P)]);
display(['The best optimal value of the objective funciton found by Math Optimizer is : ', num2str(Best_FF)]);
3. Simulation results
4. References
Abualigah, L., Diabat, A., Mirjalili, S., Abd Elaziz, M., and Gandomi, A. H. (2021). The Arithmetic Optimization Algorithm. Computer Methods in Applied Mechanics and Engineering.