NLP star sky intelligent dialogue robot series for natural language processing: in depth understanding of Transformer's multi head attention architecture for natural language processing
This paper starts with the architecture of Transformer's multi head attention layer, and then uses an example of Python coding to help readers understand the multi head attention mechanism.

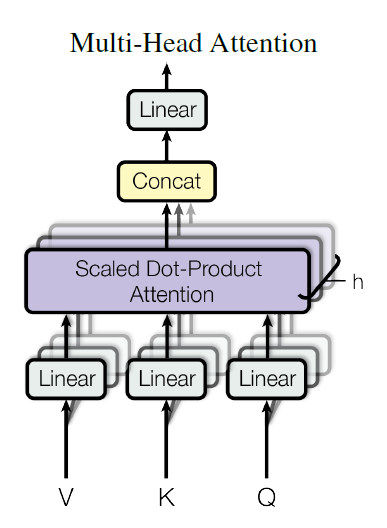
Bull attention mechanism

The multi head attention sublayer of Transformer contains 8 heads, which are respectively connected to the normalization layer for residual connection and output.

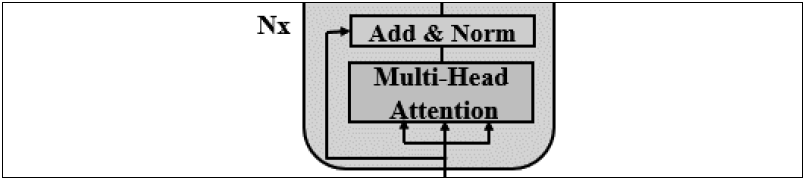
The input of the multi attention sublayer of the first layer of the encoder stack is a vector, including the embedded vector and position coding of each word.

The dimension D of the vector of each word Xn in the input sequence_ model = 512:

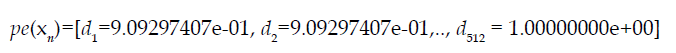
Each word in the input sequence is mapped to all other words to determine how it fits a sequence. In the following sentences, we can see that "it" may be related to "cat" and "rug"

Sequence =The cat sat on the rug and it was dry-cleaned.

The model is trained to determine that "it" is related to "cat" or "rug". The model can be trained by using the dmodel = 512 dimension, but by analyzing the sequence, only one dmodel block can be obtained at a time, which will take a lot of computing time. A better method is to divide each word Xn of all word sequences X into 8 dk = 64 dimensions according to the dmodel = 512 dimension, and then run 8 attention heads for parallel computing to speed up the training speed, Gets a different representation subspace of the relationship between each word and other words.

Now we can see that there are eight attention heads running in parallel. One attention head may think that "it" and "cat" match very well, another attention head may think that "it" and "rug" match very well, and one attention head may think that "rug" is very suitable for "dry cleaned". The output of each attention head is a matrix zi with the shape of x* dk. The output multi attention head Z matrix is defined as:

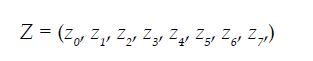
Connect the outputs of multiple attention heads to ensure that the outputs of multiple head sublayers are correct. Each attention head is connected to z with the dimension dmodel = 512

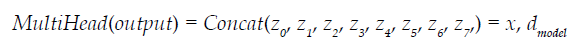
In each attention head hn of the attention mechanism, each word vector is represented by three vectors:

• Q vector query: Dimension dq = 64
• K vector key: Dimension dk = 64
• V vector value: Dimension dv = 64
  
  Calculation formula of Q vector, K vector and V vector
  
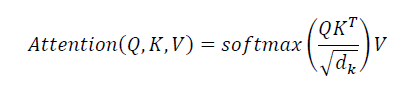
  Next, we will implement the attention mechanism in 10 steps using basic Python code, using only numpy and a softmax function.

Step 1: input vector representation

We will use the smallest Python functions to understand Transformer and focus on the internal operation of Transformer at a lower level. Import numpy and scipy packages

import numpy as np
from scipy.special import softmax

The input of the constructed attention mechanism is reduced to dmodel = 4 instead of dmodel = 512, so that the dimension of the input vector x is reduced to dmodel = 4, which is easier to visualize. X contains 3 inputs, each with 4 dimensions instead of 512:

print("Step 1: Input : 3 inputs, d_model=4")
x =np.array([[1.0, 0.0, 1.0, 0.0],   # Input 1
             [0.0, 2.0, 0.0, 2.0],   # Input 2
             [1.0, 1.0, 1.0, 1.0]])  # Input 3
print(x)

Printout results:

Step 1: Input : 3 inputs, d_model=4
[[1. 0. 1. 0.]
 [0. 2. 0. 2.]
 [1. 1. 1. 1.]]

The first step of the model is ready:

Next, we add the weight matrix to our model.

Step 2: initialize weight matrix

Each input has 3 weight matrices:

• Qw: Q vector
• Kw: K vector
• Vw: V vector

These three weighting matrices will be applied to all inputs in the model,
The weight matrix described by Vaswani et al. (2017) is dk = 64 dimensions. However, we reduce the matrix dimension to dk = 3 and set it to a weight matrix of 3 * 4. By performing point multiplication on the input x, we can more easily visualize the intermediate results.

In the three weight matrices of Q, K and V, initialization starts from the weight matrix of Q query vector:

print("Step 2: weights 3 dimensions x d_model=4")
print("w_query")
w_query =np.array([[1, 0, 1],
                   [1, 0, 0],
                   [0, 0, 1],
                   [0, 1, 1]])
print(w_query)

w_ Output result of query weight matrix:

Step 2: weights 3 dimensions x d_model=4
w_query
[[1 0 1]
 [1 0 0]
 [0 0 1]
 [0 1 1]]

Next, initialize the weight matrix of the K vector

print("w_key")
w_key =np.array([[0, 0, 1],
                 [1, 1, 0],
                 [0, 1, 0],
                 [1, 1, 0]])
print(w_key)

The output result of the weight matrix of the K vector is:

w_key
[[0 0 1]
 [1 1 0]
 [0 1 0]
 [1 1 0]]

Finally, the weight matrix of V vector is initialized

print("w_value")
w_value = np.array([[0, 2, 0],
                    [0, 3, 0],
                    [1, 0, 3],
                    [1, 1, 0]])
print(w_value)

The output result of the weight matrix of the V vector is:

w_value
[[0 2 0]
 [0 3 0]
 [1 0 3]
 [1 1 0]]

The second step of the model is ready:

Next, we multiply the weight by the input vector to get Q, K and V.

Step 3: matrix multiplication yields Q, K, V

Now we multiply the input vector by the weight matrix to get each input Q vector, K vector and V vector. In this model, for all input data, suppose there is a w_query,w_key and w_value weight matrix.

• First multiply the input vector by w_query weight matrix:

print("Step 3: Matrix multiplication to obtain Q,K,V")

print("Queries: x * w_query")
Q=np.matmul(x,w_query)
print(Q)

Vector of output result Q1= [1, 0, 2],Q2= [2,2, 2], and Q3= [2,1, 3]:

Step 3: Matrix multiplication to obtain Q,K,V
Queries: x * w_query
[[1. 0. 2.]
 [2. 2. 2.]
 [2. 1. 3.]]

Schematic diagram of Q vector point multiplication x calculation

• Now we use w_key weight matrix multiplied by input vector

print("Step 3: Matrix multiplication to obtain Q,K,V")

print("Keys: x * w_key")
K=np.matmul(x,w_key)
print(K)

Get the result of K vector K1 = [0, 1, 1], K2 = [4, 4, 0], and K3 = [2, 3, 1]:

Step 3: Matrix multiplication to obtain Q,K,V
Keys: x * w_key
[[0. 1. 1.]
 [4. 4. 0.]
 [2. 3. 1.]]

Schematic diagram of K vector point multiplication x calculation

• Finally, we multiply the input vector by w_value weight matrix

print("Values: x * w_value")
V=np.matmul(x,w_value)
print(V)

The result of obtaining V vector is: V1 = [1, 2, 3], V2 = [2, 8, 0], and V3 = [2, 6, 3]:

Values: x * w_value
[[1. 2. 3.]
 [2. 8. 0.]
 [2. 6. 3.]]

Schematic diagram of V vector point multiplication x calculation

The third step of our model is ready:

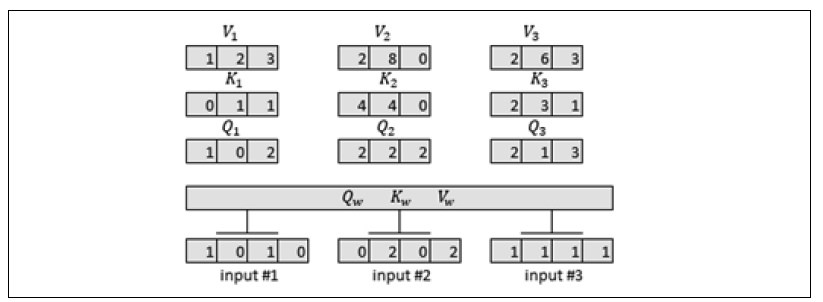
So far, we have obtained the Q K V value required to calculate the attention score.