Introduction to graph theory

Definition of graph

Graph G =(V,E),V is a finite non empty set of vertices, and E is an edge set.
V(G) and E(G) represent the vertex set and edge set of G, respectively. Where E(G) can be an empty set.
If E(G) is a set of directed edges, then G is a directed graph, otherwise it is an undirected graph.
< x, Y > represents the edge of a directed graph, which is called an arc. X is the starting point and Y is the end point. (x,y) represents the edge of an undirected graph with no specific direction.

Basic terms of Graphs

n represents the number of vertices in the graph and e represents the number of edges.
(1) Subgraph: G=(V,E) and G '= (V', e '). If V' and E 'are contained in V and e respectively, G' is a subgraph of G.

(2) Undirected complete graph and directed complete graph: for undirected graph, if there are n(n-1)/2 edges, it becomes undirected complete graph; For a directed complete graph, if there are n(n-1) arcs, it is called a directed complete graph.

(3) Sparse graph and dense graph: the key to distinguish
e < n l o g 2 n ? e<nlog_2n\quad? e<nlog2​n?
(4) Weight sum net: a graph with weight is called a net, and the weight can be marked on the edge.

(5) Adjacency point: vertices v and v 'become adjacency points / associated with each other if there is a side / arc.

(6) Degree, in degree and out degree: the degree of vertex v refers to the number of edges associated with V, which is recorded as TD(v). For directed graphs, there are also the concepts of in degree and out degree. In degree represents the number of arcs with V as the head, and out degree represents the number of arcs with V as the tail.

(7) Connected, connected graph, connected component: connected, there is a path between two vertices, that is, connected, any two vertices have a path, that is, connected graph, and non connected graph can have connected components.

(8) Strongly connected graphs: for directed graphs.

Type definition and implementation of graph - based on adjacency matrix representation

adjacency matrix

• Adjacency matrix of graph:

A [ i ] [ j ] = { 1 if < v i , v j > or ( v i , v j ) ∈ E 0 back of A[i][j]= \begin{cases} 1\qquad if < V_ i,v_ j> Or (v_i,v_j)\in E\ 0\qquad or vice versa \ end{cases} A[i][j]={1 if < vi, vj > or (vi, vj) ∈ E0, vice versa

• Adjacency matrix of network:

A [ i ] [ j ] = { w i , j if < v i , v j > or ( v i , v j ) ∈ E ∞ back of A[i][j]= \begin{cases} w_{i,j}\qquad if < v_i, v_j > or (v_i,v_j)\in E\ \infty\qquad otherwise \ end{cases} A[i][j]={wi,j if < vi, vj > or (vi, vj) ∈ E ∞, vice versa

• code implementation

#define MAXVEX 20
#define INFINITY 32768

typedef char VertexType; /* Vertex types should be user-defined  */
typedef int EdgeType; /* The weight type on the edge shall be user-defined */
typedef struct MyGraph
{
	VertexType vexs[MAXVEX]; /* Vertex table */
	EdgeType arc[MAXVEX][MAXVEX];/* Adjacency matrix can be regarded as edge table */
	int numNodes, numEdges; /* The current number of vertices and edges in the graph  */
}MyGraph;

Basic operation of diagram

• Create undirected net

  Algorithm steps:

  • Enter the total number of vertices and edges
  • Enter vertex information in turn
  • Initialize the adjacency matrix so that each weight is initialized to the maximum value
  • Construct the adjacency matrix. Input the vertices and weights attached to the edge in turn, and assign the same value at the symmetrical position. If it is a directed graph, only the vertices corresponding to the arc can be weighted.

Status CreatUDN(MyGraph& G)
{
	cout << "Enter the total number of vertices and sides, separated by spaces or enter" << endl;
	cin >> G.numNodes >> G.numEdges;
	cout << "Enter the information of vertices in turn" << endl;
	for (int i = 0; i < G.numNodes; i++)
		cin >> G.vexs[i];
	//Initialize the adjacency matrix and set the weights to the maximum
	for (int i = 0; i < G.numNodes; i++)
		for (int j = 0; j < G.numNodes; j++)
			G.arc[i][j] = INFINITY;	//If it is a graph, set INFINITY to 0
	cout << "Enter the vertex and weight of an edge" << endl;
	for (int k = 0; k < G.numEdges; k++)
	{
		VertexType v1, v2;
		EdgeType w;
		cin >> v1 >> v2 >> w;
		int i = LocateVex(G, v1), j = LocateVex(G, v2);
		G.arc[i][j] = w;			//If it is a graph, it can be assigned as 1
		G.arc[j][i] = G.arc[i][j];	//If it is a directed net or a directed graph, just note this line
	}
	return OK;
}

• Return vertex position
  Finds whether the vertex u is within G. if it is, returns the vertex position; otherwise, returns - 1.

int LocateVex(MyGraph G,VertexType u)
{
	for (int i = 0; i < G.numNodes; i++)
		if (u == G.vexs[i])
			return i;
	return -1;
}

• Find first neighbor pin

  Find out whether the vertex has an adjacent point. If so, return the adjacent node position; otherwise, return - 1.

int FirstAdjVex(MyGraph G, int v)
{
	for (int i = 0; i < G.numNodes; i++)
	{
		if (G.arc[v][i] != INFINITY)
			return i;
	}
	return -1;
}

• Find next neighbor pin

  Give the current adjacency point and find out whether the vertex has the next adjacency point. If so, return the vertex position; otherwise, return - 1.

int NextAdjVex(MyGraph G, int v, int w)
{
	for (int i = w + 1; i < G.numNodes; i++)
	{
		if (G.arc[v][i] != INFINITY)
			return i;
	}
	return -1;
}

• Adjacency matrix of output graph

  Ergodic output adjacency matrix array

  void PrintfUDN(MyGraph G)
  {
  	for (int i = 0; i < G.numNodes; i++)
  	{
  		for (int j = 0; j < G.numNodes; j++)
  			cout << G.arc[i][j] << "=>";
  		cout << endl;
  	}
  }
  

Depth first traversal of Graphs

Algorithm Introduction

• Starting from a vertex v in the graph, access vertex v first. At this time, record visited[v] = true.
• For connected graphs: start from the unreachable adjacency points of v in turn, and traverse the graph in depth first until the vertices connected with v in the graph are accessed.
• For non connected graphs: if there are still unreachable vertices in the graph at this time, start from an unreachable vertex and repeat the depth first traversal until all vertices in the graph are accessed.
• It can be implemented by stack structure or recursion

Algorithm implementation

//Connected graph
void DFS(MyGraph G, int v)
{
	cout << G.vexs[v]; visited[v] = true;
	for (int w = FirstAdjVex(G, v); w >= 0; w = NextAdjVex(G, v, w))
	{
		if (!visited[w])
			DFS(G, w);
	}
}
//Unconnected graph
void DFSTraverse(MyGraph G)
{
	for (int v = 0; v < G.numNodes; v++)
	{
		visited[v] = false;
	}
	for (int v = 0; v < G.numNodes; v++)
	{
		if (!visited[v])
			DFS(G,v);
	}
}
//adjacency matrix 
void DFSMyGraph(MyGraph G, int v)
{
	for (int v = 0; v < G.numNodes; v++)
	{
		visited[v] = false;
	}
	cout << G.vexs[v]; visited[v] = true;
	for (int w = 0; w < G.numNodes; w++)
	{
		if ((G.arc[v][w] != INFINITY) && (!visited[w]))
			DFS(G, w);
	}
}

Breadth first traversal of Graphs

Algorithm Introduction

• Those close to node v are accessed first, first in first out, which is consistent with the idea of queue
• Starting from a vertex v in the graph, first access vertex v and put V into queue Q. at this time, record visited[v] = true.
• For connected graph: the vertices in queue Q are out of the queue, and the unreachable adjacency points in the graph are accessed in turn. If there are unreachable vertices, they are placed in queue Q until queue q is empty
• For non connected graphs: if there are still unreachable vertices in the graph, start from an unreachable vertex and repeat breadth first traversal until all vertices in the graph are accessed.

Algorithm implementation

//For Connected Graphs
void BFS(MyGraph G, int v)
{
	MySqQueue Q;
	for (int v = 0; v < G.numNodes; v++)
	{
		visited[v] = false;
	}
	cout << G.vexs[v]; visited[v] = true;
	InitQueue(Q);
	EnQueue(Q, v);
	while (!QueueEmpty(Q))
	{
		int u;
		DeQueue(Q, u);
		for (int w = FirstAdjVex(G, u); w >= 0; w = NextAdjVex(G, u, w))
		{
			if (!visited[w])
			{
				cout << G.vexs[w]; visited[w] = true;
				EnQueue(Q, w);
			}
		}
	}
}
//For unconnected graphs
void BFSTraverse(MyGraph G)
{
	for (int v = 0; v < G.numNodes; v++)
	{
		visited[v] = false;
	}
	for (int v = 0; v < G.numNodes; v++)
	{
		if (!visited[v])
			BFS(G, v);
	}
}
//adjacency matrix 
void BFSMyGraph(MyGraph G, int v)
{
	for (int v = 0; v < G.numNodes; v++)
	{
		visited[v] = false;
	}
	BFS(G, w);
}

BFS and DFS experimental validation

• Test code

#include "Graph.h"
MyGraph graph;
int main()
{
	CreatUDN(graph);
	PrintfUDN(graph);
	system("pause");
	cout << "Depth first traversal by node:" << endl;
	for (int i = 0; i < graph.numNodes; i++)
	{
		cout << "\n To node"<<graph.vexs[i]<<"start" << endl;
		DFSMyGraph(graph, i);
	}
	system("pause");
	DFSTraverse(graph);
	system("pause");
	cout << "Breadth first traversal by node:" << endl;
	for (int i = 0; i < graph.numNodes; i++)
	{
		cout << "\n To node" << graph.vexs[i] << "start" << endl;
		BFSMyGraph(graph,i);
	}
	system("pause");
	BFSTraverse(graph);
	system("pause");
}

• Connected graph & unconnected graph

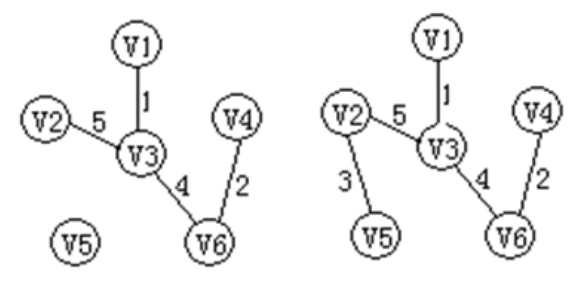
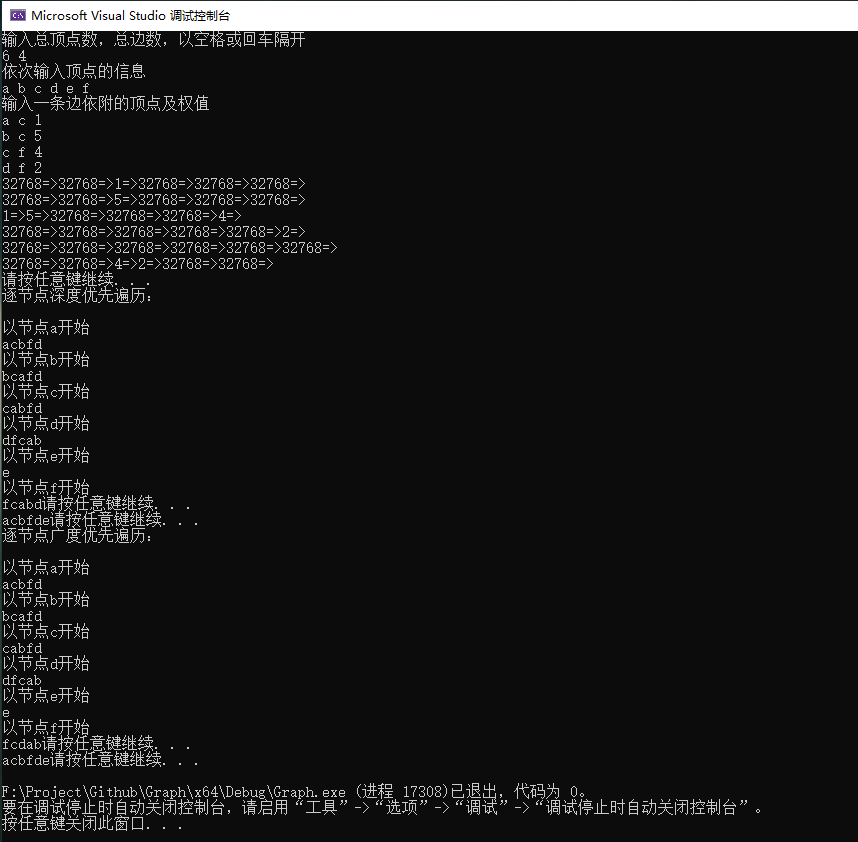
• Experimental phenomenon

  • Unconnected graph
    
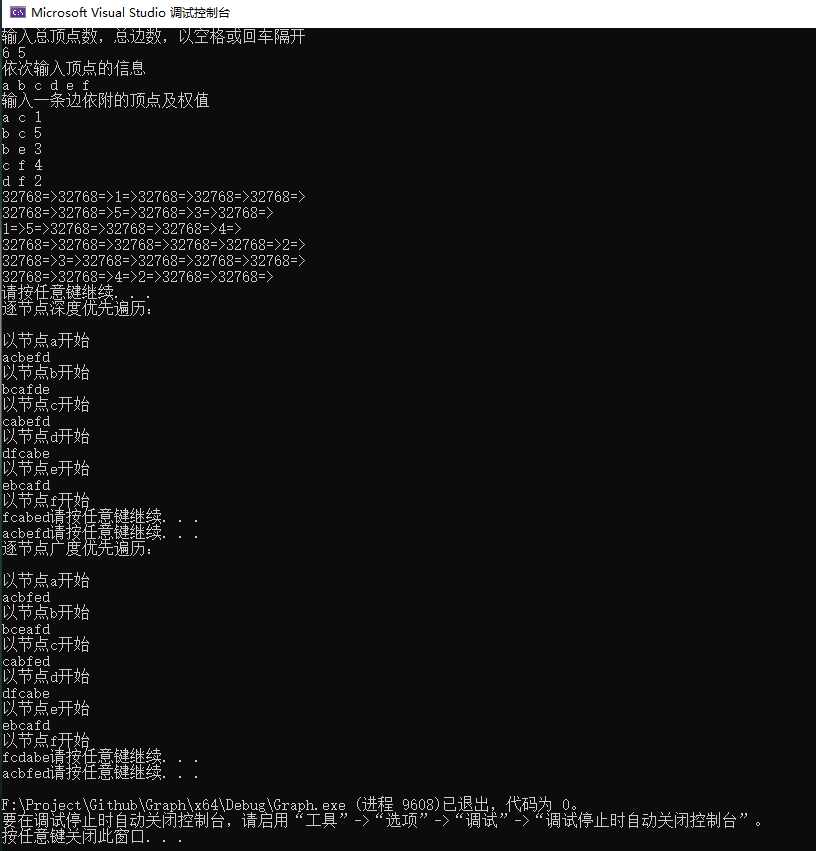
  • Connected graph