catalogue
2021 Huawei written test first
Cache forwarding packet statistics (100%)
2021 Huawei written examination question 2
Find instance knowledge in the knowledge map (100%)
2021 Huawei written test question 3
2021 Huawei written test first
Cache forwarding packet statistics (100%)
Title Description
There is a forwarding queue of k nodes. The forwarding capacity of each node is m and the caching capacity is n (it means that this node can immediately forward m packets, the remaining cache can cache up to n packets, and then the remaining packets will be discarded, and the cached packets will continue to be forwarded in the next round). In addition, some nodes in this queue may need to skip forwarding directly due to failure, but there will not be two consecutive failed nodes. The operation is divided into two rounds. The first round sends a packet to this queue for forwarding; In the second round, the direct drive allows the cached packets to continue forwarding.
Find the minimum total number of data packets that may be received in the last two rounds (if there are still data packets in the second round of cache, the cache packets will be discarded) 1 < = k < = 40 1 < = m, n < = 1000 1 < = a < = 1000
For example, there are two nodes, node 1 (forwarding capacity m:50, caching capacity n:60) and node 2(m:30, n:25). The number of packets sent is 120.
When there is no node failure:
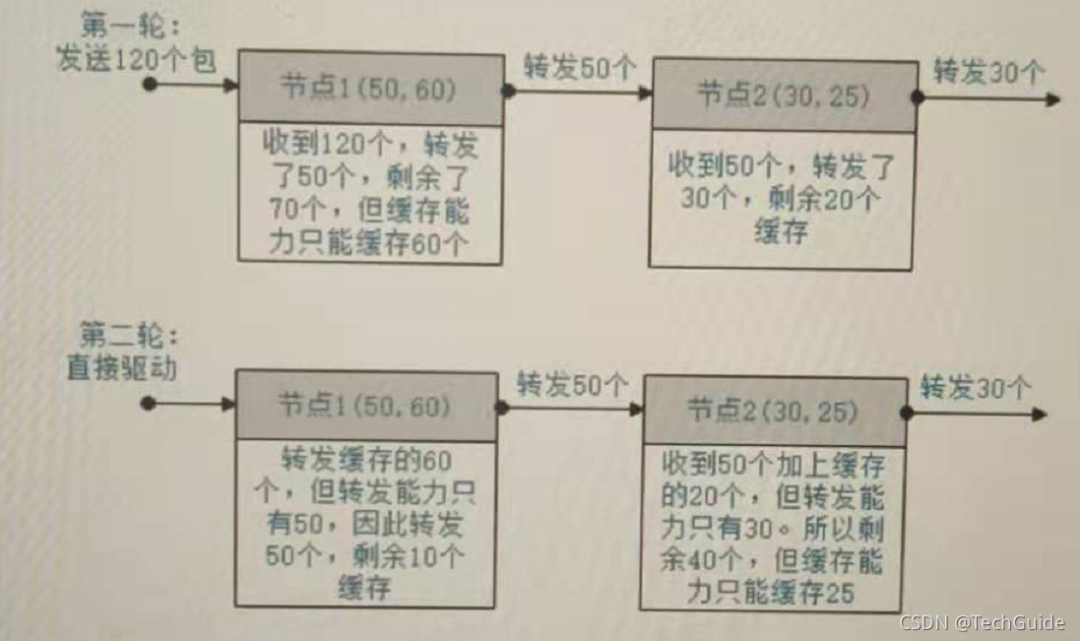
Input Description: the first line has a queue length of k, and the second line is an array of k node forwarding capabilities, separated by spaces. m. N is separated by commas, for example, the number of packets in the third row of 10, 20, 11, 21, 12, 22 a
2 50,60 30,25 120
Output Description:
55
Explanation: refer to the legend in the title. When the first node fails, only the second node forwards and receives the least packets.
Problem solving ideas:
Bilevel dynamic programming.
1. First, define vector < vector < int > > cap (K + 1, vector < int > (2)), and save the forwarding capacity and cache capacity of each node; (the input node is the 0th node)
2. Define vector < vector < int > > DP (K + 1, vector < int > (2)), and save the first forwarding quantity and the second forwarding quantity of each node. (the first forwarding quantity of the input node is a, and the second forwarding quantity is 0)
3. Calculate (dpfun()) the number of send1 and send2 forwarded for the first and second time by each node:
The number of the first forwarding is the number of the first forwarding received from the previous node and the minimum value of the forwarding capacity of the node:
cur_cap[0]: refers to the forwarding capability of the current node, cur_cap[1]: the cache capacity of the current node, that is, dp_fun() passed in cap[i].
pre[0]: the number of the first forwarding of the previous node, pre[1]: the number of the second forwarding of the previous node, that is, dp_fun() passed in cap[i].
send1 = min(pre[0], cur_cap[0]);
The number of second forwarding needs to be discussed by case, that is, whether all the first forwarding from the previous node are transferred. However, the maximum forwarding quantity is the minimum value of forwarding capacity and cache capacity plus the second forwarding quantity of a node.
send2 = min(pre[1] + cur_cap[1], cur_cap[0]);
If the number of the first forwarding of the previous node is greater than the forwarding capacity of the current node (with cache), the number of the second forwarding of the current node is the number of the second forwarding of the previous node plus the first cache of the current node:
send2 = min(pre[1] + pre[0] - cur_cap[0], send2);
Otherwise, the second forwarding of the current node is the second forwarding of the previous node:
send2 = min(pre[1], send2);
4. Analyze the node failure again. Because there will be no two consecutive node failures, traverse all nodes, cross forward, and then take the smaller one for each node forwarding.
vector<int> res1 = dpfun(dp[i - 1], cap[i]);// The previous node is not faulted
vector<int> res2 = dpfun(dp[i - 2], cap[i]);// Previous node failure
dp[i] = res1[0] + res1[1] <= res2[0] + res2[1] ? res1 : res2;
5. Output the smaller value of the forwarding quantity of the last node or the penultimate node.
res = min(dp[k][0] + dp[k][1], dp[k - 1][0] + dp[k - 1][1]);
Reference code:
#include<bits/stdc++.h>
using namespace std;
//According to the packet sent by the previous node and the capability of the current node
//Calculate the packets sent by the current node
//pre: quantity forwarded by the previous node (twice), cur_cap: current node (forwarding capacity, cache capacity)
vector<int> dpfun(vector<int> &pre, vector<int> &cur_cap) {
int send1 = min(pre[0], cur_cap[0]);//Number of packets sent for the first time
int send2 = min(pre[1] + cur_cap[1], cur_cap[0]);//Maximum possible number of packets sent for the second time
//Judge whether the packet forwarded for the first time has been transferred
if (pre[0] - cur_cap[0] > 0)//The incoming packet is greater than the forwarding capacity of the current node
send2 = min(pre[1] + pre[0] - cur_cap[0], send2);
else
send2 = min(pre[1], send2);
return vector<int> {send1, send2};
}
int main() {
int k, a;//Number of nodes k number of packets sent a
int res = 0;//The minimum number of packets that can be forwarded in two rounds
vector<vector<int>> cap;//Cap (k, vector < int > (2)) node capability array
cap.push_back(vector<int>{0, 0});//The head node does not need to consider capacity
cin >> k;
int m1, n1;//m1 forwarding capability n1 caching capability
char ch;
for (int i = 0; i < k; i++) {
cin >> m1 >> ch >> n1;
cap.push_back(vector<int>{m1, n1});
}
cin >> a;
vector<vector<int>> dp(k + 1, vector<int>(2));//Number of packets sent twice by the ith node
dp[0][0] = a;//The 0th node sends a packet for the first time
dp[0][1] = 0;//The 0 node sends 0 packets for the second time
dp[1] = dpfun(dp[0], cap[1]);
res = min(dp[0][0] + dp[0][1], dp[1][0] + dp[1][1]);//If there is only one node
if (k == 0)
cout << a << endl;
else {
for (int i = 2; i <= k; i++) {
vector<int> res1 = dpfun(dp[i - 1], cap[i]);//The previous node is not faulted
vector<int> res2 = dpfun(dp[i - 2], cap[i]);//Previous node failure
dp[i] = res1[0] + res1[1] <= res2[0] + res2[1] ? res1 : res2;
}
res = min(dp[k][0] + dp[k][1], dp[k - 1][0] + dp[k - 1][1]);
cout << res << endl;
}
return 0;
}2021 Huawei written examination question 2
Find instance knowledge in the knowledge map (100%)
Knowledge map is a structured semantic network, which is used to describe the relationship between concepts and instances in the physical world. The knowledge map can be regarded as a directed graph. The points in the graph are concepts or instances, and the edges in the graph are the correlation between concepts and instances.
A simple knowledge map is defined
Concepts: including parent and child concepts. Parent and child concepts can have multiple levels through subcalassof relationship Association; Example: only concepts are associated through instanceOf relationship: relationship: it is expressed in the form of triples, which is a string with spaces as the separator between members. For example, "student subclass of person" means that student is a sub concept of person, and "apple instanceOf fruit" means that apple is an instance of the concept fruit. Given a knowledge map, please write a method to find all instances of a concept. If a concept has sub concepts, the returned result needs to include instances of all its sub concepts; If the input concept has no instance, the string "empty" is returned (Note: the output string text does not need to contain quotation marks).
The given graph satisfies the following limitations: 1. There is no loop in the directed graph. 2. The definitions of all points and relationships are case sensitive
Input Description: enter the first line, which indicates the number n of relationships in the atlas. The value range [110000] is from line 2 to line n+1, which indicates the relationships in the atlas. Each line is a relationship triple. Line n+2 represents the meta node to be found and the point existing in the relationship triple. The length of each line of characters shall not exceed 100.
3 student subClassOf person Tom inslenceOf student Marry instanceOf person person
The output describes an array of strings arranged in ascending dictionary order. Its contents are all instances of the concept and its sub concepts.
Marry Tom
Explanation: student is a sub concept of person, Tom is an instance of student, and Mary is an instance of person. Mary's dictionary order is less than Tom, so Mary Tom is returned.
Solution idea 1:
Find whether its parent node is target according to instanceOf.
1. Whether subclass of or instancOf, the child node is on the left and the parent node is on the right.
2. Define hash set hash_set(instance) stores the child nodes of instancOf (the first input of each pair).
3. Define the hash map unordered_map(hash) stores all instanceOf and sunClassOf.
4. According to hash_set can traverse whether its parent node can reach the target node. If it meets the requirements, it will be stored in set and sorted by default. If not, keep looking for the parent relationship until the relationship ends.
5. Because the storage nodes that meet the instance exist in the set and are ordered. So output directly without sorting.
That is, a map is used to store relationships, and a set is used to store instances. Then traverse each instance. If its parent node or always traverse to the parent relationship, if it can find an instance equal to the target concept, the instance meets the requirements and exists in the set.
Reference code 1:
#include <bits/stdc++.h>
using namespace std;
int main(int argc,char* argv[]){
int n;
cin>>n;
unordered_map<string,string> hash;//val is the parent node
unordered_set<string> instance;//Store instacnOf
string s1,s2,s3;
for(int i=0;i<n;++i){
cin>>s1>>s2>>s3;
if(s2=="instanceOf")
instance.insert(s1);
hash[s1]=s3;
}
string ss;
cin>>ss;
set<string> ret;
for(auto s:instance){
string s1=s;
while(hash.count(s1)){
if(hash[s1]==ss){
ret.insert(s);
break;
}
s1=hash[s1];
}
}
if(ret.size()==0){
cout<<"empty"<<endl;
}else{
int i=0;
for(auto s:ret){
if(i==0) cout<<s;
else cout<<" "<<s;
++i;
}
}
return 0;
}Problem solving idea 2:
Recursive implementation
1. Define two map s to store instance and subClass respectively.
map<string, vector<string>> subClass;// Storing subClassOf relationships may be one to many
map<string, vector<string>> instance;// Storing instanceOf relationships may be one to many
2. Find up recursively from child nodes
Reference code 2:
#include<bits/stdc++.h>
using namespace std;
void solve(map<string, vector<string>> &subClass, map<string, vector<string>> &instance, vector<string> &res, string &target) {
for (string str : instance[target])
res.push_back(str);
for (string str : subClass[target])
solve(subClass, instance, res, str);
return;
}
int main() {
int n;
cin >> n;
map<string, vector<string>> subClass;//Storing subClassOf relationships may be one to many
map<string, vector<string>> instance;//Storing instanceOf relationships may be one to many
for (int i = 0; i < n; i++) {
string head;
cin >> head;
string relation;
cin >> relation;
string tail;
cin >> tail;
if (relation == "subClassOf")
subClass[tail].push_back(head);
else
instance[tail].push_back(head);
}
string target;
cin >> target;
vector<string> res;
solve(subClass, instance, res, target);
sort(res.begin(), res.end());
if (res.empty())
cout << "empty";
else {
for (string str : res)
cout << str << " ";
}
cout << endl;
return 0;
}2021 Huawei written test question 3
Lake connectivity (100%)
Title Description
There are many lakes on the map. In order to enhance the anti rainstorm capacity of lakes, channels need to be dug between lakes to make them connected (diagonal is regarded as disconnected). Some lands are hard stones, and the energy required to dig through is twice that of ordinary lands, that is, the length of an ordinary grid is 1 and the length of a grid with hard stones is 2. The map is represented by a two-dimensional matrix. There are only three possibilities for each location. 0 is a lake, 1 is ordinary land, 2 is hard stones, and the maximum map is MN. It is necessary to return the shortest channel to dig through all lakes. If the channel does not exist, return 0. Limit: the maximum number of M and N is 20, and the number of lakes does not exceed 11.
Input Description: the first row is m, the second row is N, and the third row starts with the map matrix of M*N
5 4 0 1 1 0 0 1 0 0 0 1 0 0 0 1 0 1 1 1 1 1
Output Description: returns the shortest channel to dig through all lakes
1
Explanation: there are two lakes on the map. You only need to dig through one land and two lakes can be connected.
Problem solving ideas:
This problem is a classic example of [Steiner tree]. Steiner tree is a kind of problem: several (generally about 10) points on an undirected graph with edge weight are [key points]. It is required to select some edges so that these points are in the same connecting block, and at the same time, it is required to minimize the edge weight sum of the selected edges.
How to solve the Steiner tree problem In fact, it is a kind of pressure DP.
dp[i][j] indicates that node I is the root and the current state is j (the corresponding position of the point already connected with I in the binary of j is 1).
Where did i come from? In fact, i can be any point in the Unicom block without additional restrictions. Just introduce this i.
When the root I does not change (i.e. merging two connected blocks containing I), the state transition equation is:
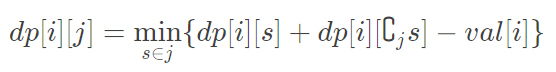
Reference code:
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <iostream>
#include <queue>
#define space putchar(' ')
#define enter putchar('\n')
using namespace std;
typedef long long ll;
template <class T>
void read(T &x){
char c;
bool op = 0;
while(c = getchar(), c < '0' || c > '9')
if(c == '-') op = 1;
x = c - '0';
while(c = getchar(), c >= '0' && c <= '9')
x = x * 10 + c - '0';
if(op) x = -x;
}
template <class T>
void write(T x){
if(x < 0) putchar('-'), x = -x;
if(x >= 10) write(x / 10);
putchar('0' + x % 10);
}
const int INF = 0x3f3f3f3f;
int n, m, K, root, f[101][1111], a[101], ans[11][11];
bool inq[101];
typedef pair<int, int> par;
typedef pair<par, int> rec;
#define fi first
#define se second
#define mp make_pair
#define num(u) (u.fi * m + u.se)
rec pre[101][1111];
const int dx[] = {0, 0, -1, 1};
const int dy[] = {1, -1, 0, 0};
queue<par> que;
bool legal(par u){
return u.fi >= 0 && u.se >= 0 && u.fi < n && u.se < m;
}
void spfa(int now){
while(!que.empty()){
par u = que.front();
que.pop();
inq[num(u)] = 0;
for(int d = 0; d < 4; d++){
par v = mp(u.fi + dx[d], u.se + dy[d]);
int nu = num(u), nv = num(v);
if(legal(v) && f[nv][now] > f[nu][now] + a[nv]){
f[nv][now] = f[nu][now] + a[nv];
if(!inq[nv]) inq[nv] = 1, que.push(v);
pre[nv][now] = mp(u, now);
}
}
}
}
void dfs(par u, int now){
if(!pre[num(u)][now].se) return;
ans[u.fi][u.se] = 1;
int nu = num(u);
if(pre[nu][now].fi == u) dfs(u, now ^ pre[nu][now].se);
dfs(pre[nu][now].fi, pre[nu][now].se);
}
int main(){
read(n), read(m);
memset(f, 0x3f, sizeof(f));
for(int i = 0, tot = 0; i < n; i++)
for(int j = 0; j < m; j++){
read(a[tot]);
if(!a[tot]) f[tot][1 << (K++)] = 0, root = tot;
tot++;
}
for(int now = 1; now < (1 << K); now++){
for(int i = 0; i < n * m; i++){
for(int s = now & (now - 1); s; s = now & (s - 1))
if(f[i][now] > f[i][s] + f[i][now ^ s] - a[i]){
f[i][now] = f[i][s] + f[i][now ^ s] - a[i];
pre[i][now] = mp(mp(i / m, i % m), s);
}
if(f[i][now] < INF)
que.push(mp(i / m, i % m)), inq[i] = 1;
}
spfa(now);
}
write(f[root][(1 << K) - 1]), enter;
dfs(mp(root / m, root % m), (1 << K) - 1);
for(int i = 0, tot = 0; i < n; i++){
for(int j = 0; j < m; j++)
if(!a[tot++]) putchar('x');
else putchar(ans[i][j] ? 'o' : '_');
enter;
}
return 0;
}