🌲 This article is included in the column Confused algorithm ——From today on, we have crossed the barrier of data structure and algorithm
Recommended by other high-quality columns:
📚Technical expert cultivation ——Engage in technology, enter big factories and talk about the three in one column of life
📚leetcode 300 questions ——An algorithm problem every day is necessary for entering a large factory
📚Design patterns in source code ——Perfect combination of theory and Practice
📚Learning python from actual combat ——Python crawler, automation, AI and other practical applications (open source code)
Click to jump to the end of the text Receive fan benefits
Hello, everyone, I'm one~
Today brings you Confused algorithm The second issue of the column - explanation of sorting algorithm. I believe that no matter for beginners or large factory interviews, sorting algorithm is indispensable. Even if you haven't learned the algorithm, you won't be unfamiliar with bubble sorting.
Today, one will take you through the barrier of "sorting algorithm". Nanny level tutorial suggestions collection. ⭐ ️
Source code address of this article: "Eight sorting" source code , extraction code: 5ehp
get ready
As the old saying goes, "before soldiers and horses move, food and grass go first". To understand the "sorting algorithm" one by one, it is recommended to prepare the following code template first.
📢 To watch this tutorial, you need to know the basic loop syntax, two number exchange, double pointer and other pre knowledge.
📚 It is recommended to read the code and analyze it step by step before trying to write it yourself.
- Create a new Java project. The whole article is also based on the implementation code of Java language.
- Create the following directory structure
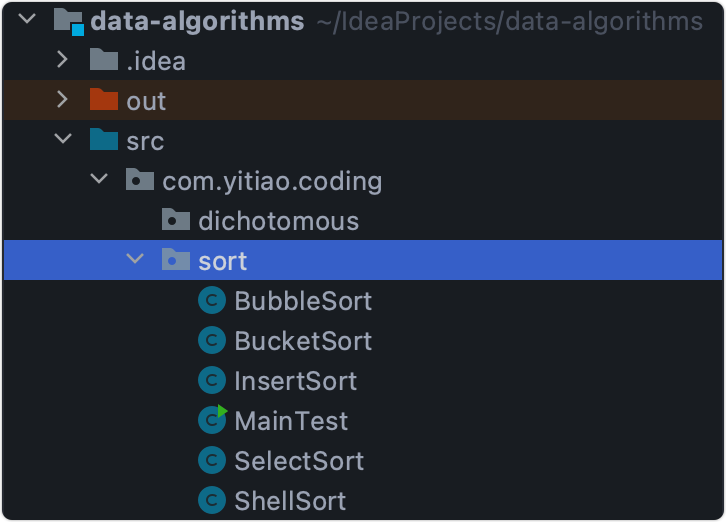
- Write a test template in the MainTest test class.
/**
* Test class
* Author: One
* Date: 2021/09/23
*/
public class MainTest {
public static void main(String[] args) {
//Sequence to be sorted
int[] array={6,10,4,5,2,8};
//Call different sorting algorithms
// BubbleSort.sort(array);
// Create an array of 100000 random data
int[] costArray=new int[100000];
for (int i = 0; i < 100000; i++) {
// Generate a number of [0100000]
costArray[i] = (int) (Math.random() * 100000);
}
Date start = new Date();
//Too long, comment out first and print step by step
//BubbleSort.sort(costArray);
Date end = new Date();
System.out.println("Time consuming:"+(end.getTime()-start.getTime())/1000+"s");
}
}
This code mainly has two functions:
- Call different sorting algorithms for testing
- Test the time required for different sorting algorithms to arrange 10w numbers in order. More concretely understand the different time complexity
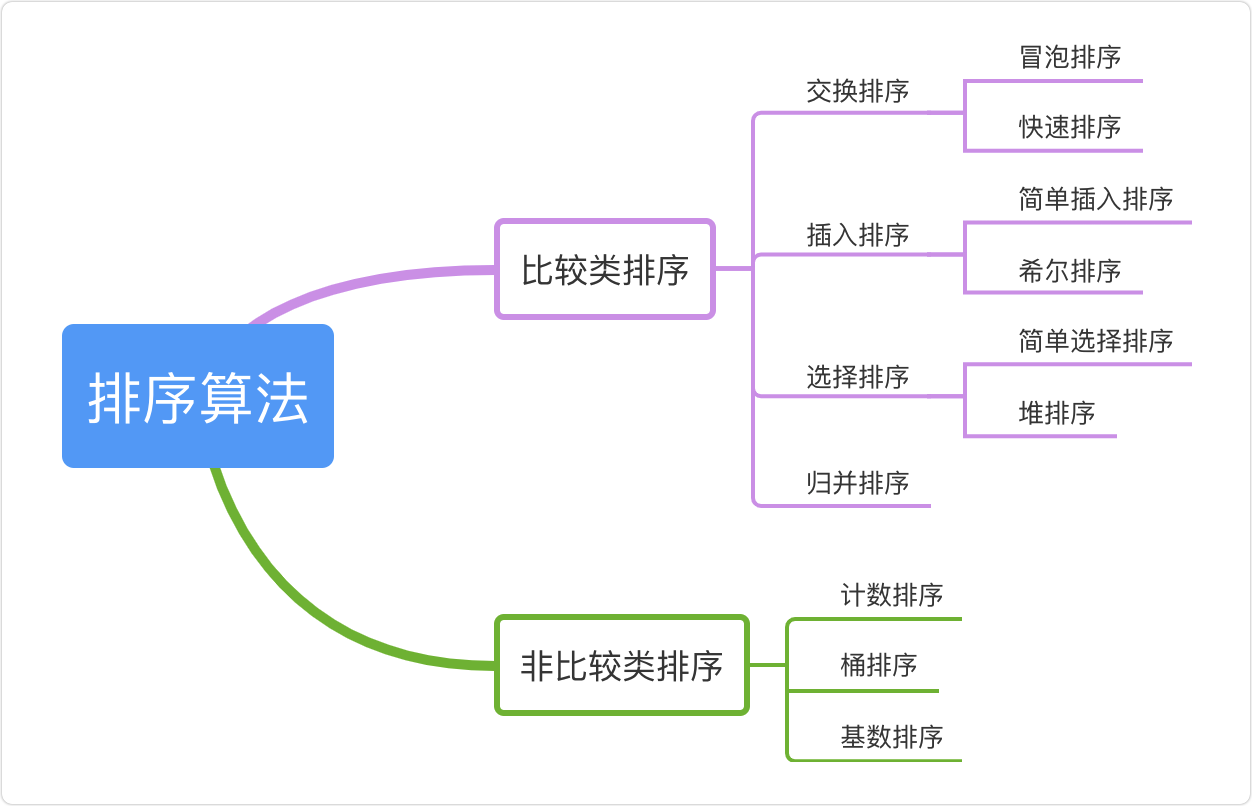
Bubble sorting
basic thought
By traversing the disordered sequence from front to back, the values of adjacent elements are compared in turn. If the reverse order is found, it is exchanged, so that the elements with large values gradually move from front to back.
Gradually rising like bubbles under the water.

Dynamic diagram explanation
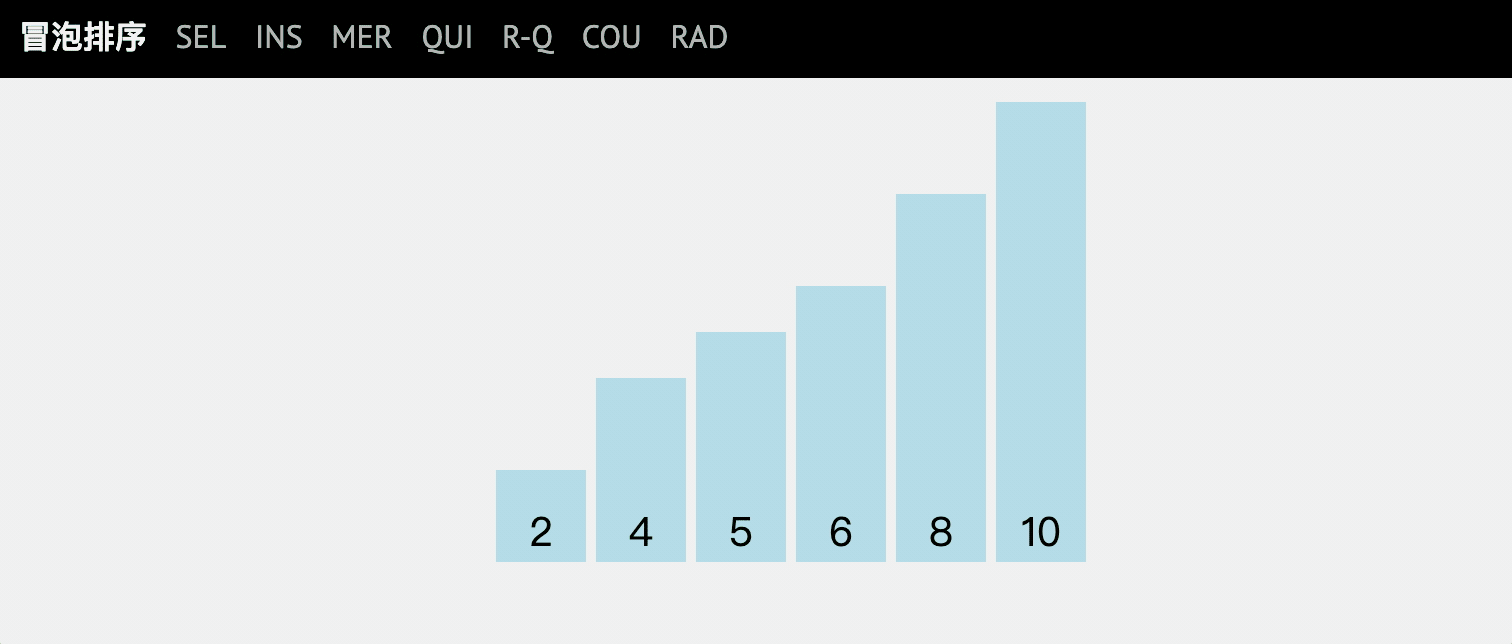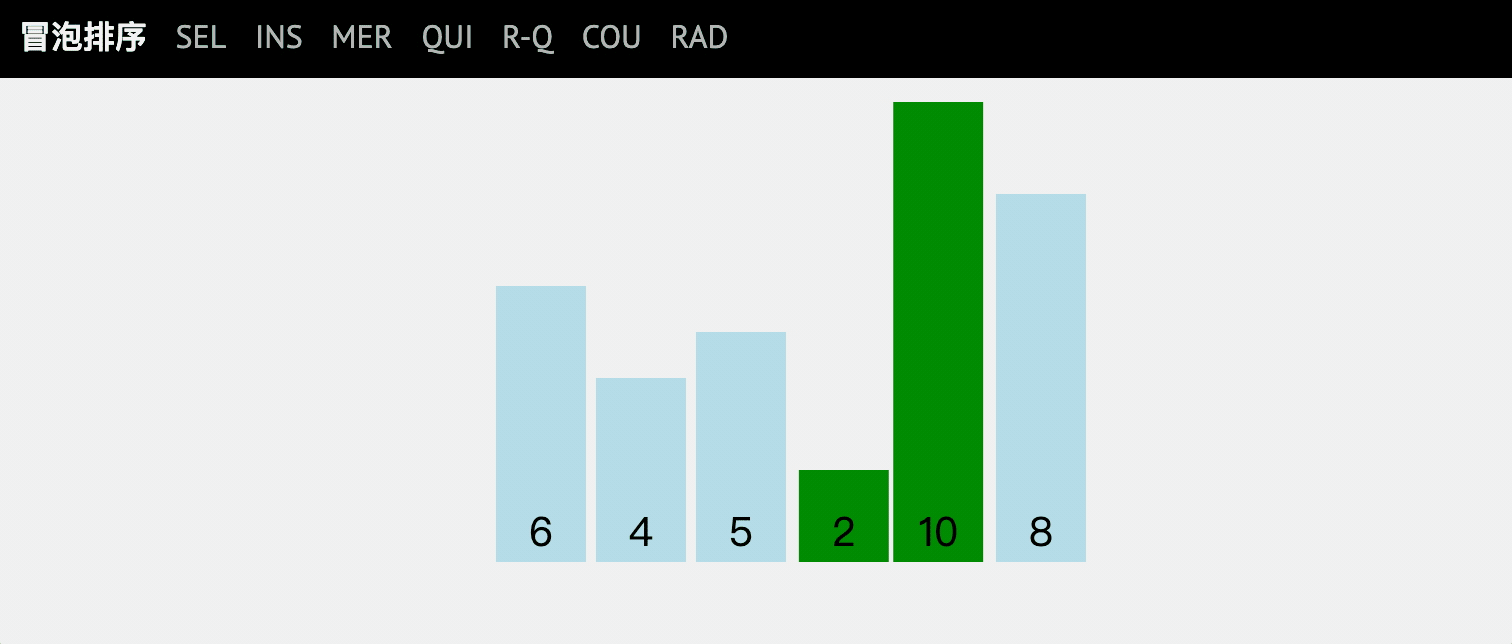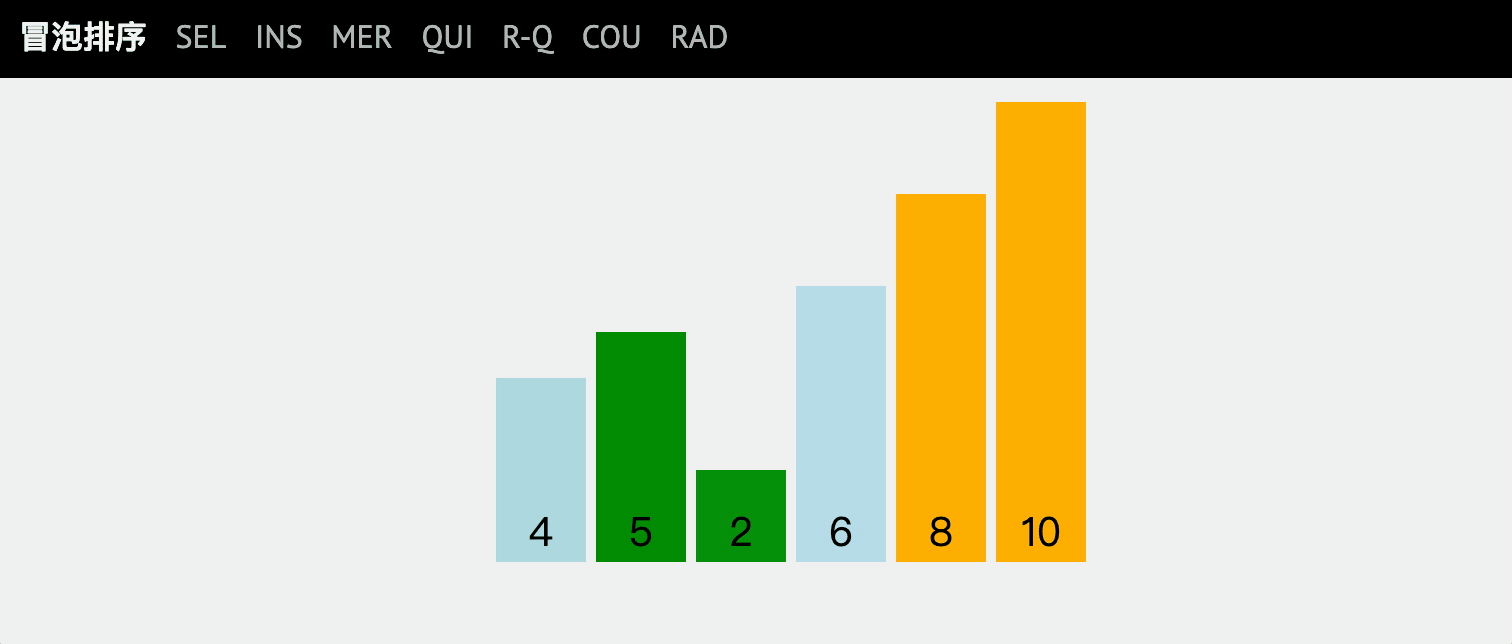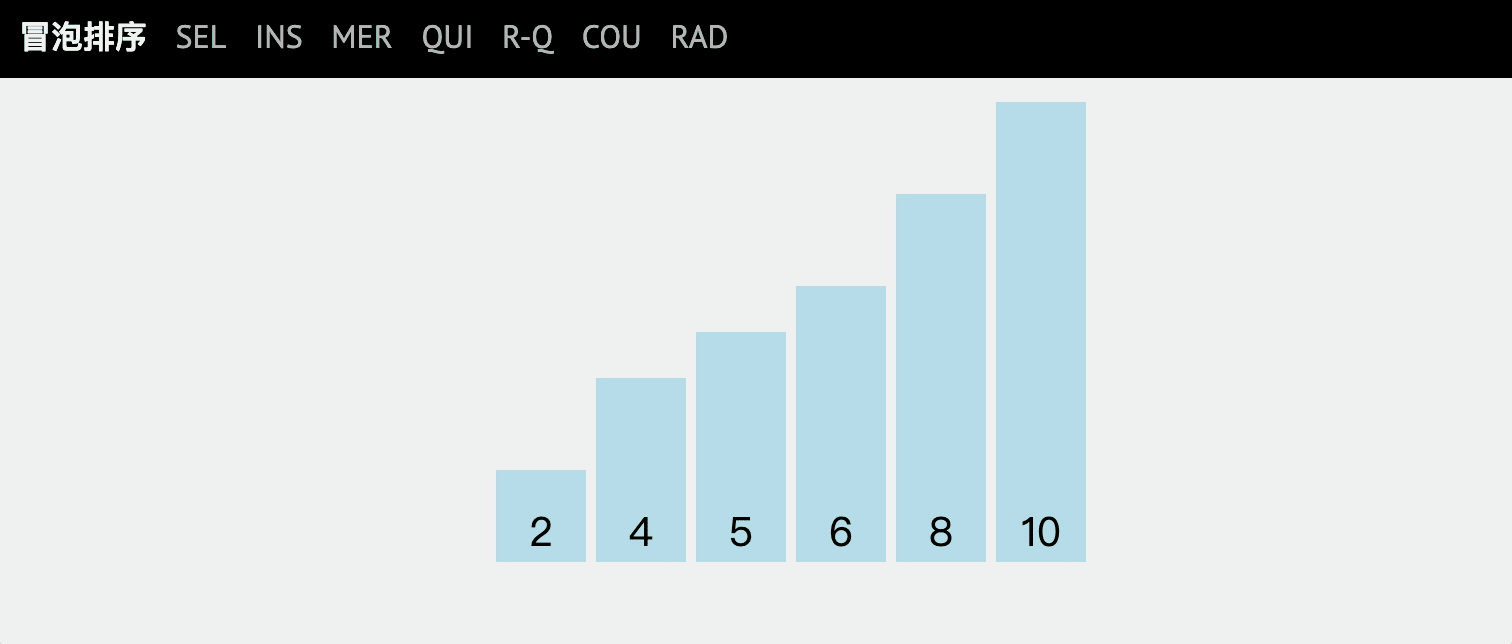
code implementation
If you don't understand, you can use the debug mode to analyze step by step.
/**
* Bubble sorting
* Author: One
* Date: 2021/09/23
*/
public class BubbleSort{
public static int[] sort(int[] array){
for (int i = 0; i < array.length; i++) {
for (int j = 0; j < array.length-1; j++) {
//Compare in turn and swap the largest elements to the last
if (array[j]>array[j+1]){
// Exchange two values with the temporary variable temp
int temp=array[j];
array[j]=array[j+1];
array[j+1]=temp;
}
}
//Output the sorting result of each step
System.out.println(Arrays.toString(array));
}
return array;
}
}
Output results
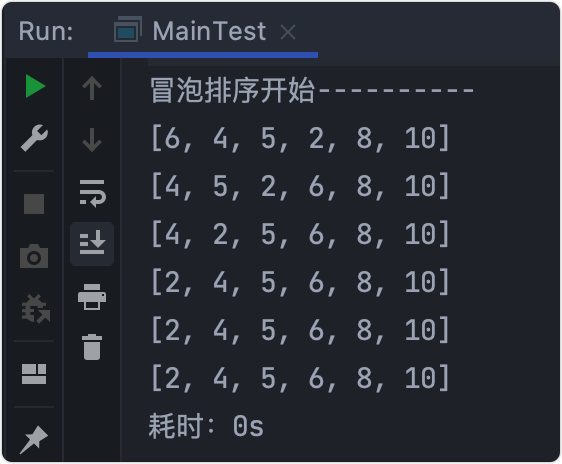
Stepwise analysis
- Initial array: [6,10,4,5,2,8]
- 6 take it out and compare it with the last 10. If 6 < 10, there is no need to exchange. - > j + +;
- 10 compare it with the latter 4, 10 > 4, exchange. - > [6,4,10,5,2,8]
- Execute the comparison exchange between j + + and the latter in turn.
- After the first layer i circulates, print the first line - > [6, 4, 5, 2, 8, 10], and the last 10 is in the correct position. - > i++
- Starting from 4, continue to compare and exchange, and the penultimate 8 returns to the correct position.
- Cycle as above - >
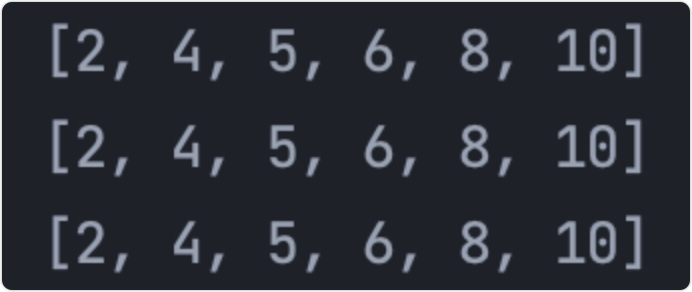
- Final result - > [2, 4, 5, 6, 8, 10]
At this time, go back to the dynamic diagram to understand.
Time consuming test
Remember to comment out the sorting class first and print the code step by step.
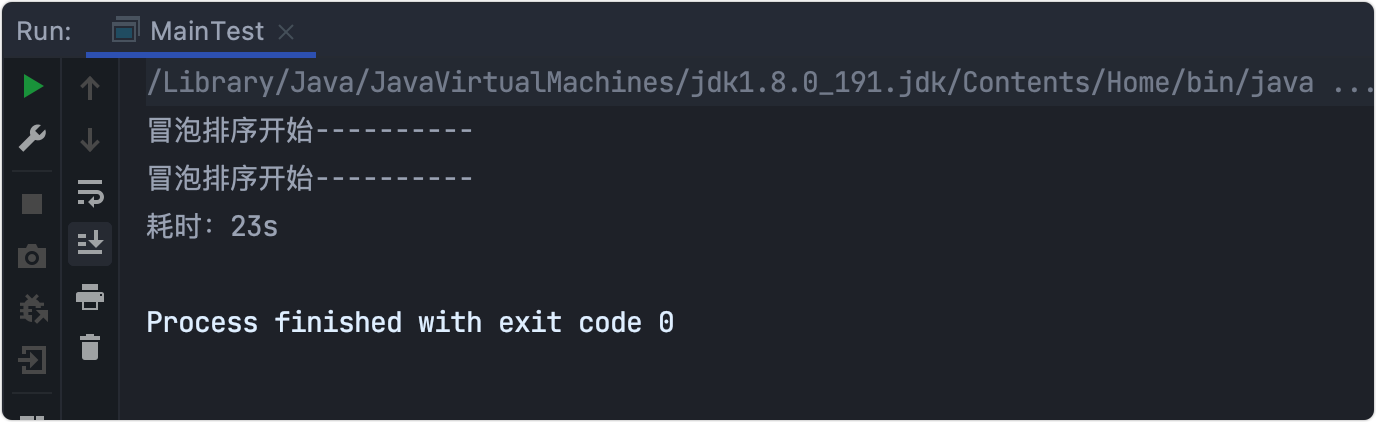
Time complexity: O(n^2)
Algorithm optimization
Optimization point I
After the first traversal of the outer layer, the last bit is correct, and j does not need to be compared, so the end condition should be changed to j-i-1;.
Optimization point 2
In the sorting process, each element is constantly approaching its own position. If there is no exchange after a comparison, it indicates that the sequence is orderly. Therefore, a flag should be set in the sorting process to judge whether the elements have been exchanged, so as to reduce unnecessary comparison.
Optimize code
public static int[] sortPlus(int[] array){
System.out.println("Optimize bubble sort start----------");
for (int i = 0; i < array.length; i++) {
boolean flag=false;
for (int j = 0; j < array.length-i-1; j++) {
if (array[j]>array[j+1]){
flag=true;
int temp=array[j];
array[j]=array[j+1];
array[j+1]=temp;
}
}
if (flag==false){
break;
}
// System.out.println(Arrays.toString(array));
}
return array;
}
Optimization test
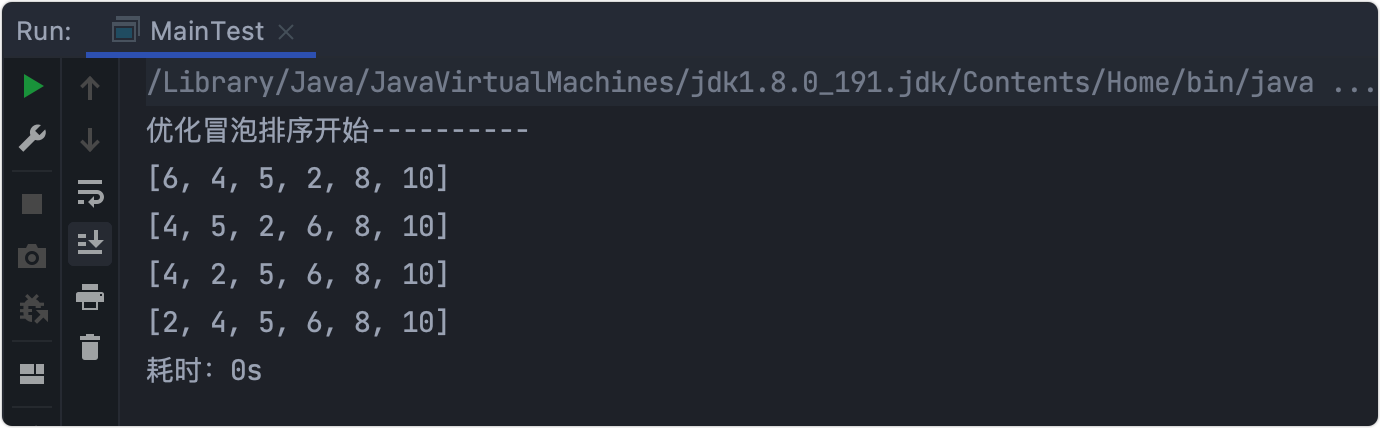
Through the basic test, we can see that when the sequence has been ordered, that is, no exchange occurs, the cycle is terminated.
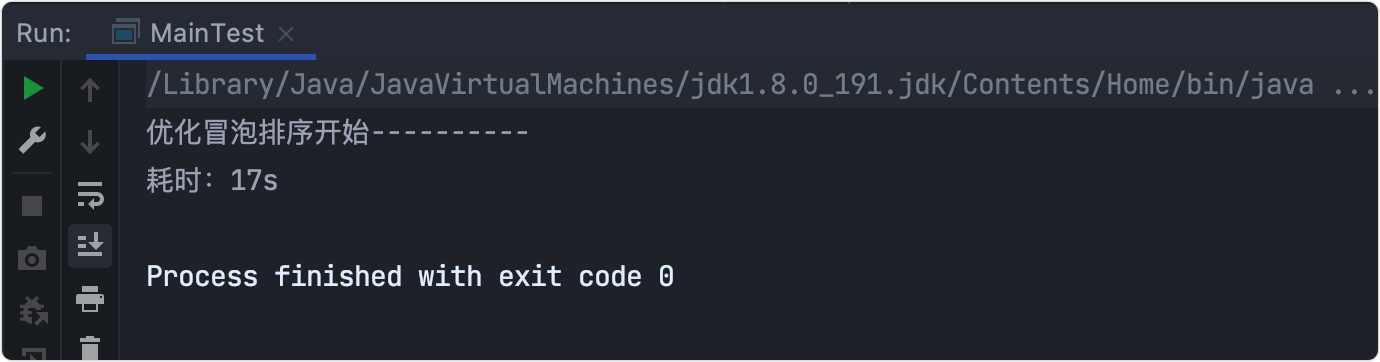
The time-consuming test is optimized from 27s to 17s.
Select sort
basic thought
Selective sorting is very similar to bubble sorting. It is to select an element according to the specified rules from the data of disorderly sequence, and then exchange positions according to the regulations to achieve the purpose of sorting.
Dynamic diagram explanation
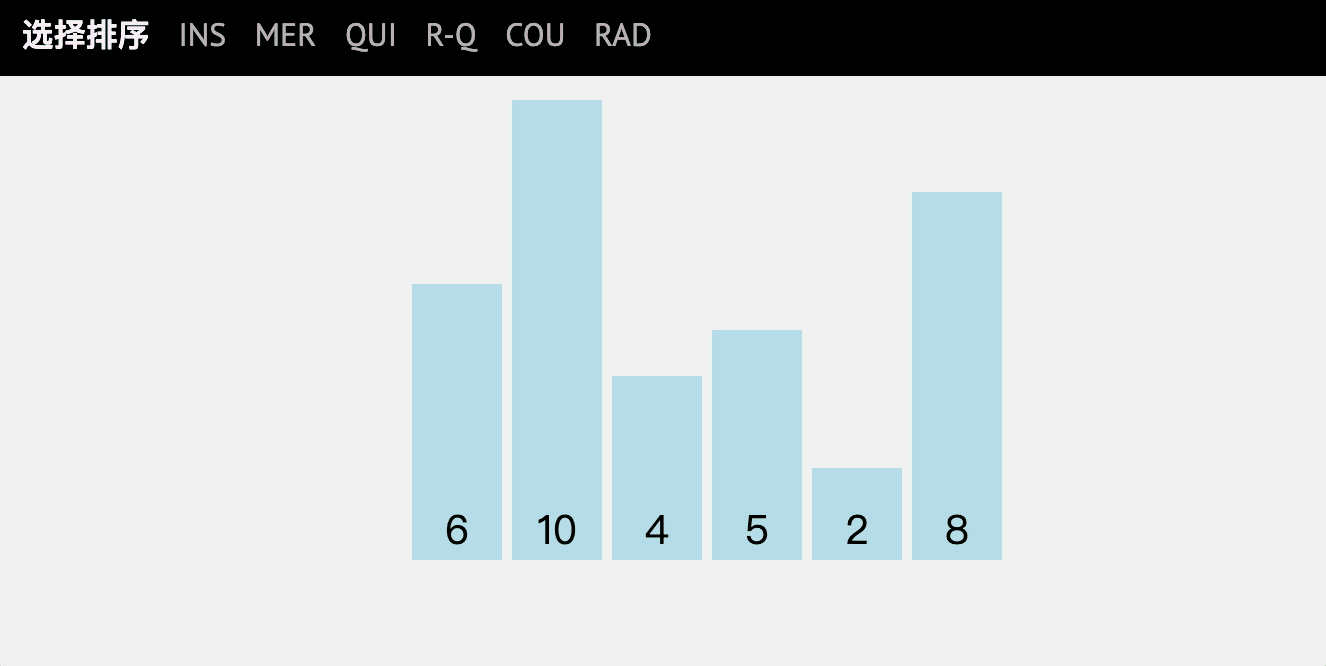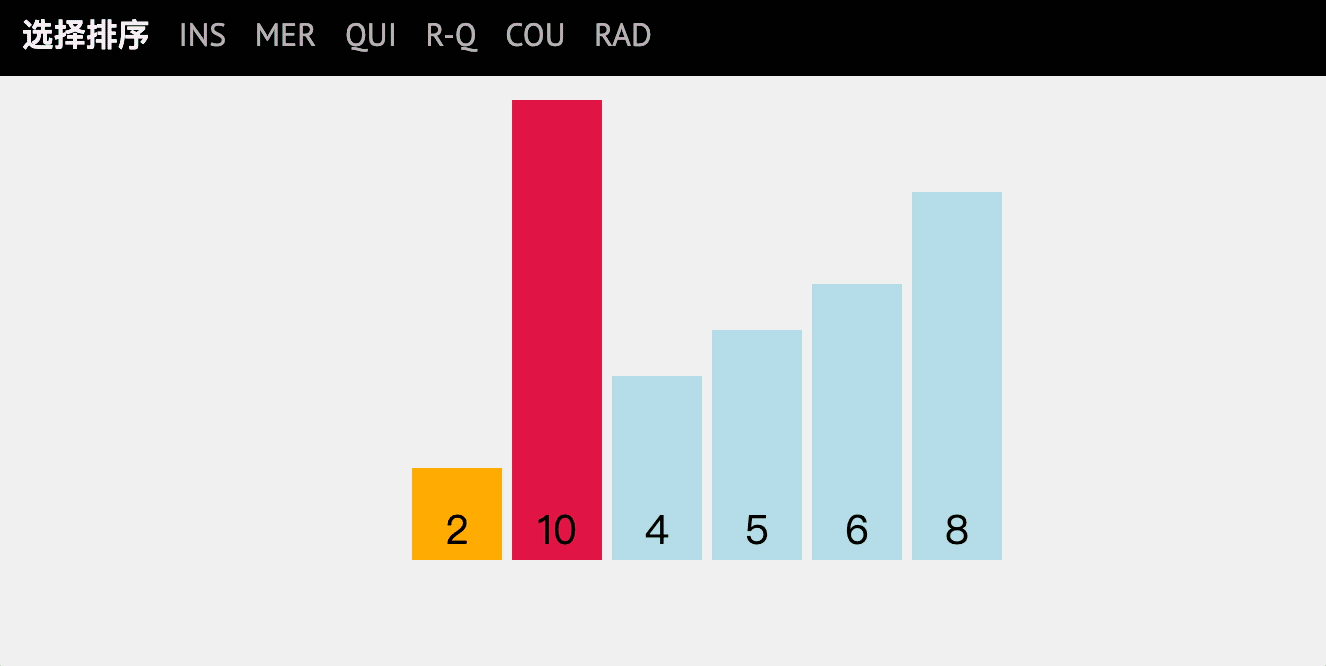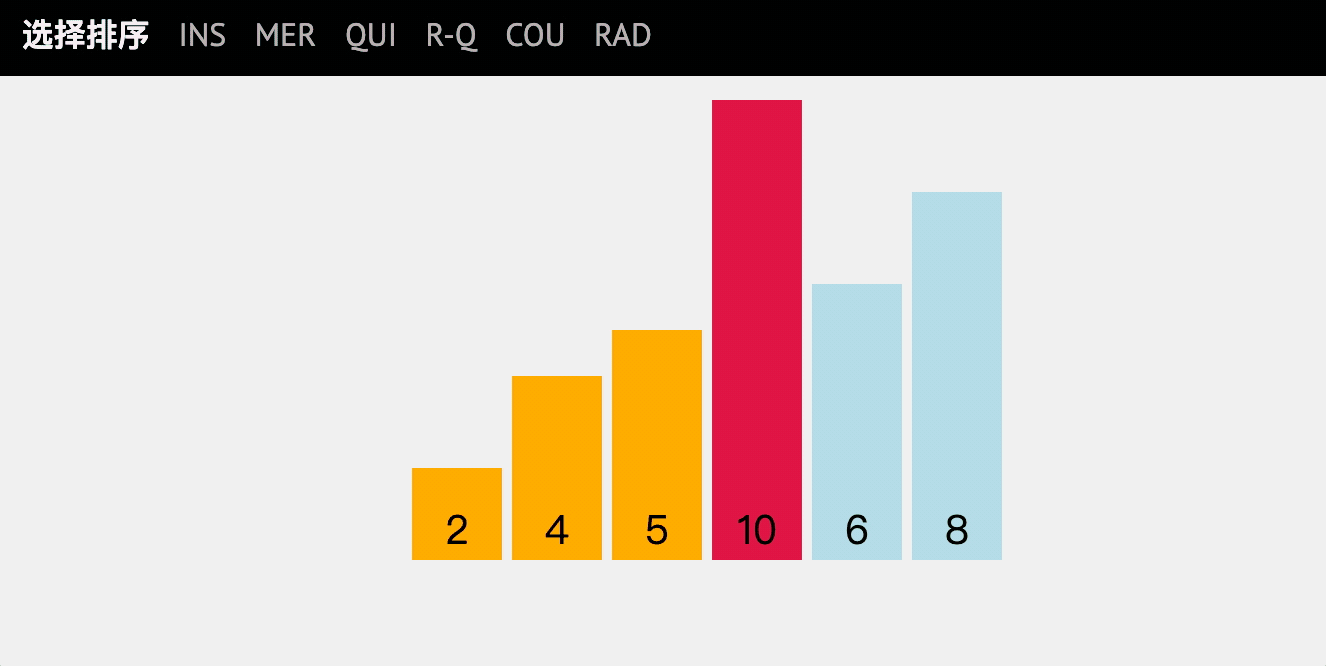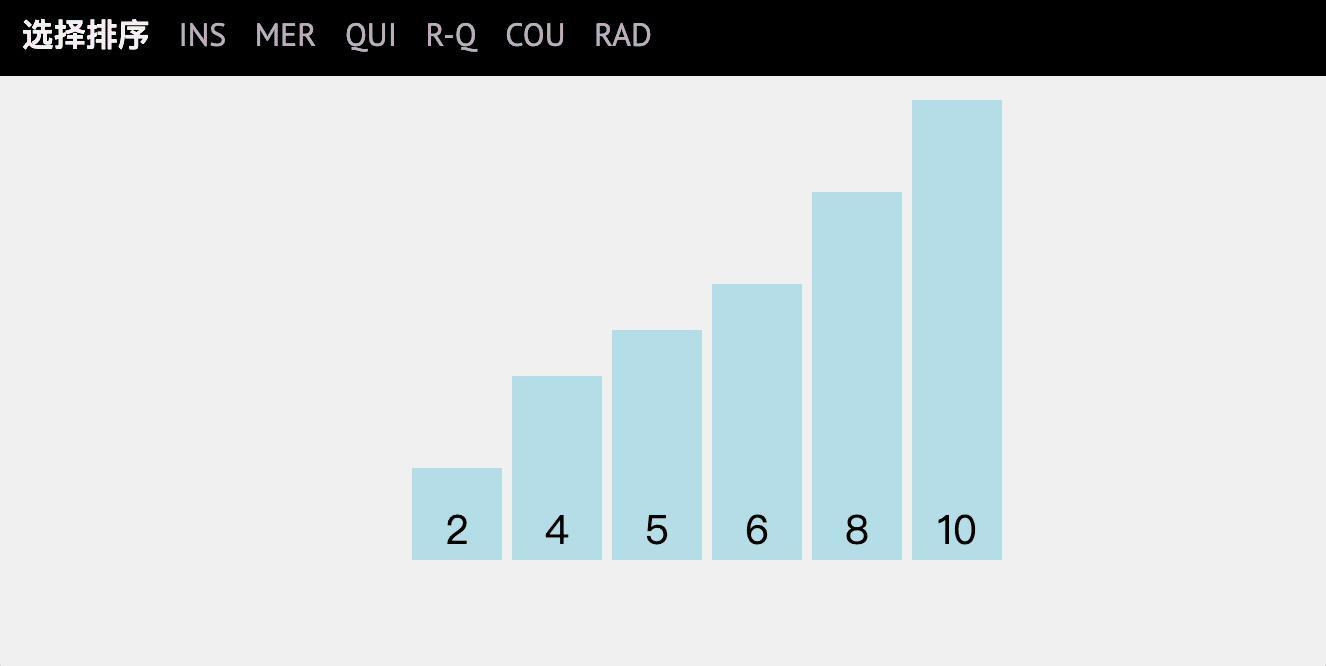
code implementation
public class SelectSort {
public static int[] sort(int[] array) {
System.out.println("Select sort start----------");
for (int i = 0; i < array.length; i++) {
//Each value only needs to be compared with the value after it, so start from
for (int j = i; j < array.length; j++) {
//Note which two values are compared here
if (array[i]>array[j]){
int temp=array[i];
array[i]=array[j];
array[j]=temp;
}
}
System.out.println(Arrays.toString(array));
}
return array;
}
}
Output results
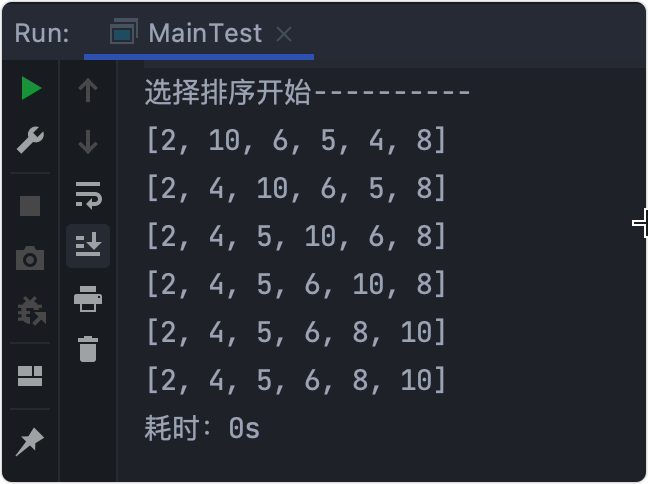
Stepwise analysis
- Initial array: [6,10,4,5,2,8]
- Compare 6 with 10 without exchanging - > J++
- 6 compared with 2, exchange - > J++
- Note that at this time, you continue to compare with 2 without exchanging. Make sure that the first bit (the smallest number) is 2 - > I++
- Loop down and find the number of the first small, the second small
- Final result - > [2, 4, 5, 6, 8, 10]
At this time, go back to the dynamic diagram to understand.
Time consuming test
Time complexity: O(n^2)
Algorithm optimization
The appeal code uses the exchange method to find smaller values, and can also be moved, that is, only exchange once after all comparisons.
There will be some gain in the occupancy of space, but there is little gain in time, which can be ignored and will not be demonstrated.
Insert sort
basic thought
The N disordered elements are regarded as an ordered table and an unordered table. At the beginning, the ordered table contains only one element, and the unordered table contains n-1 elements. In the sorting process, a local correct solution is obtained by continuously inserting elements into the ordered table, and the length of the ordered column is gradually expanded until the sorting is completed.
Dynamic diagram explanation
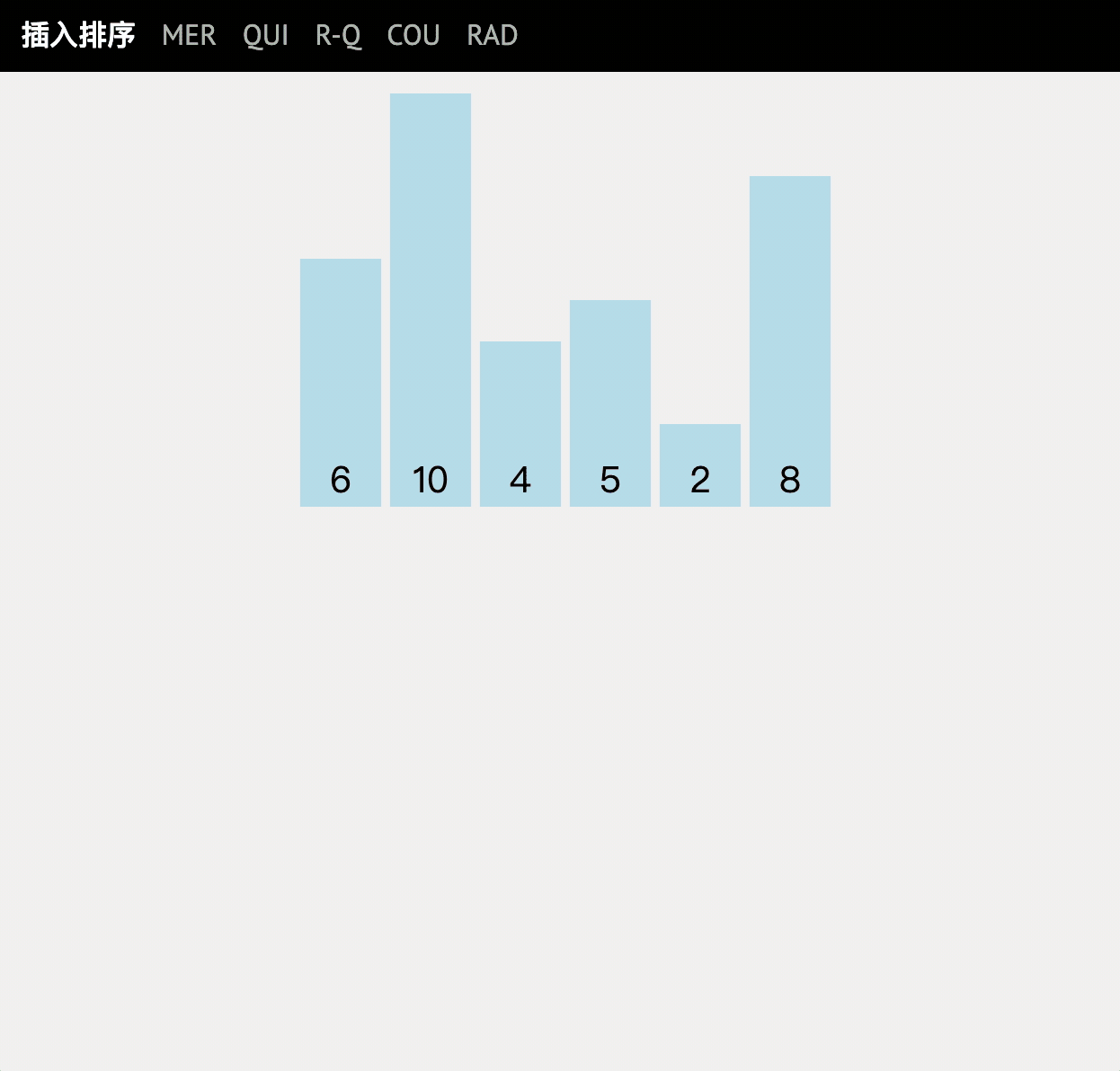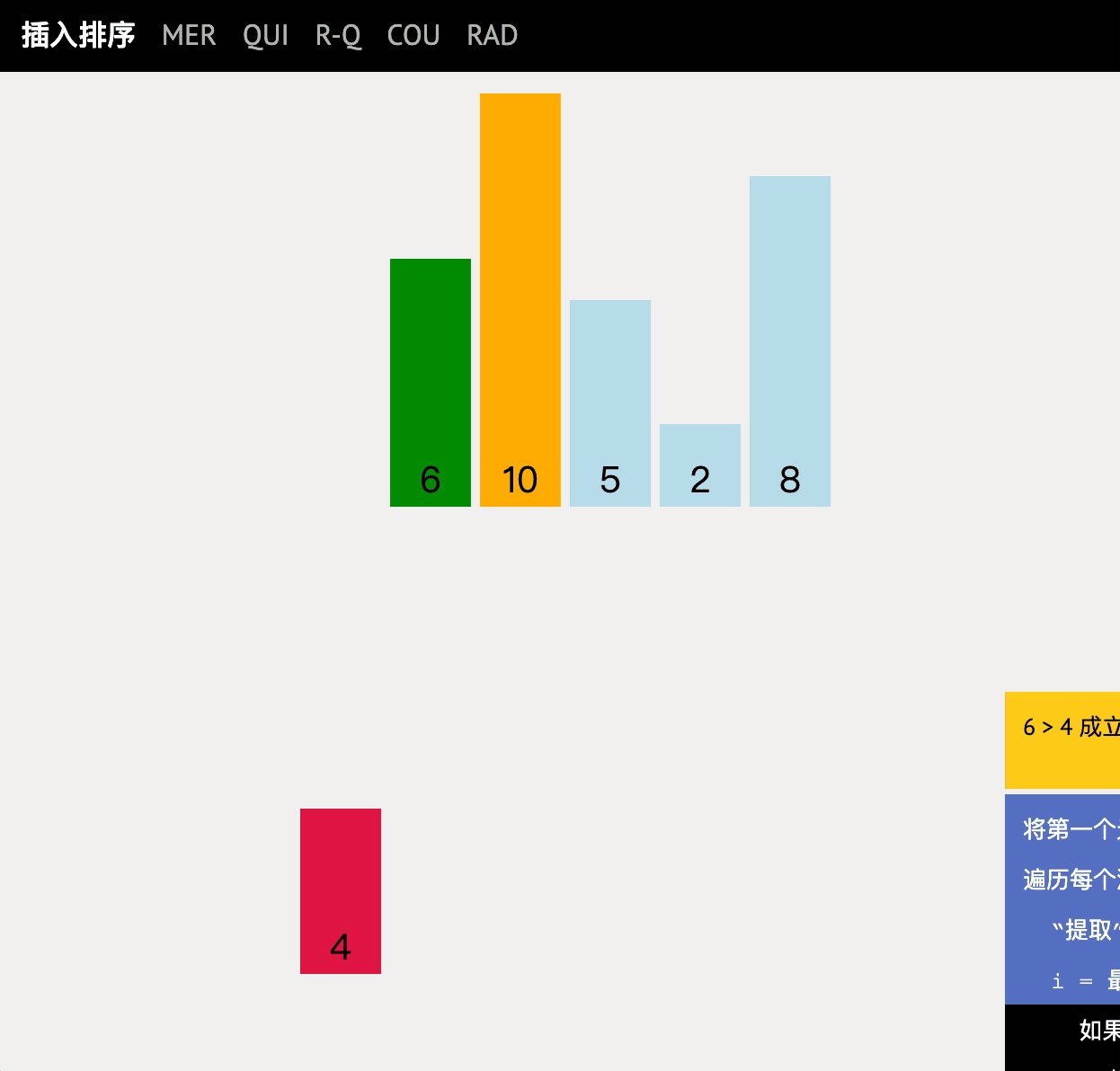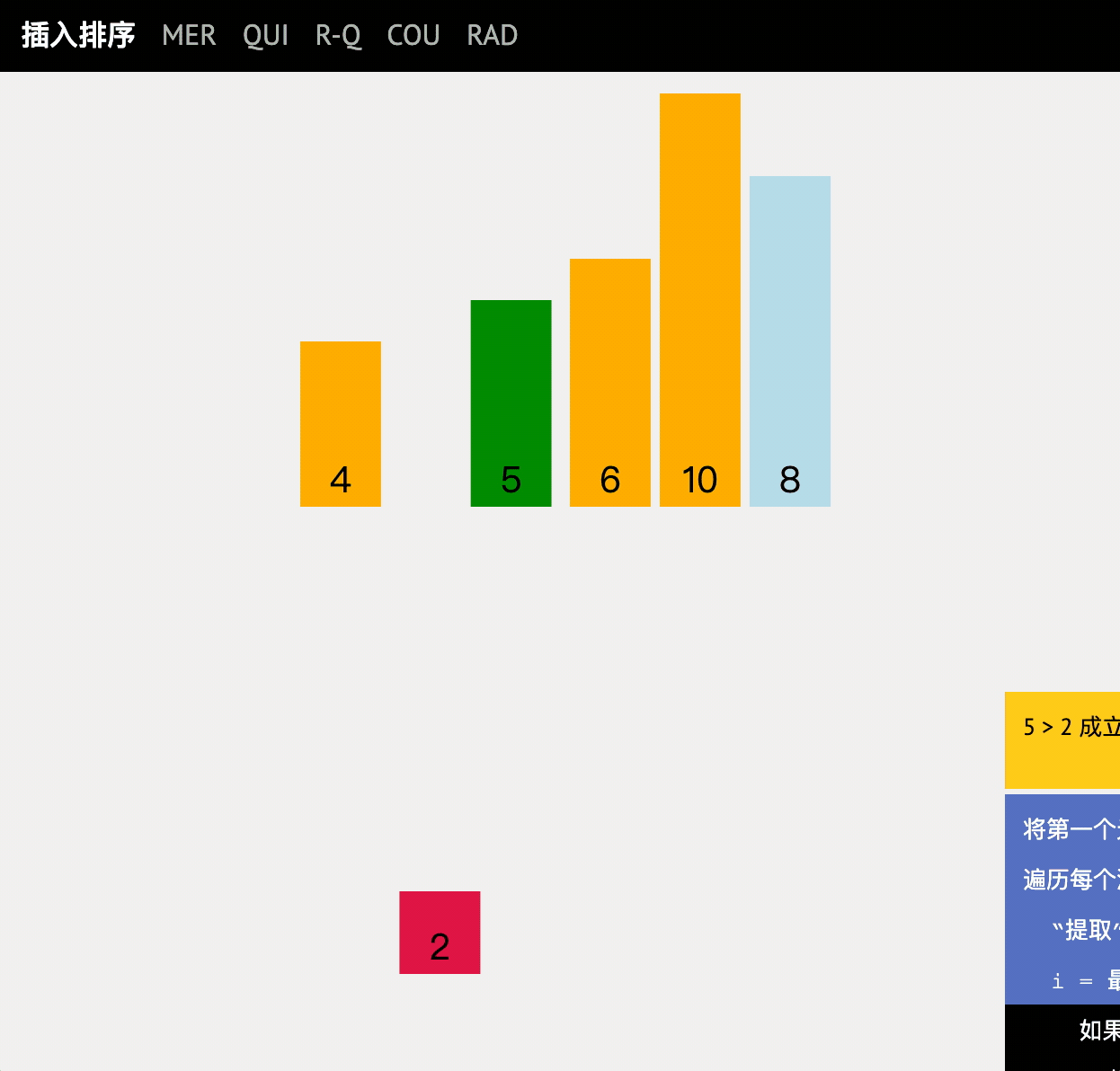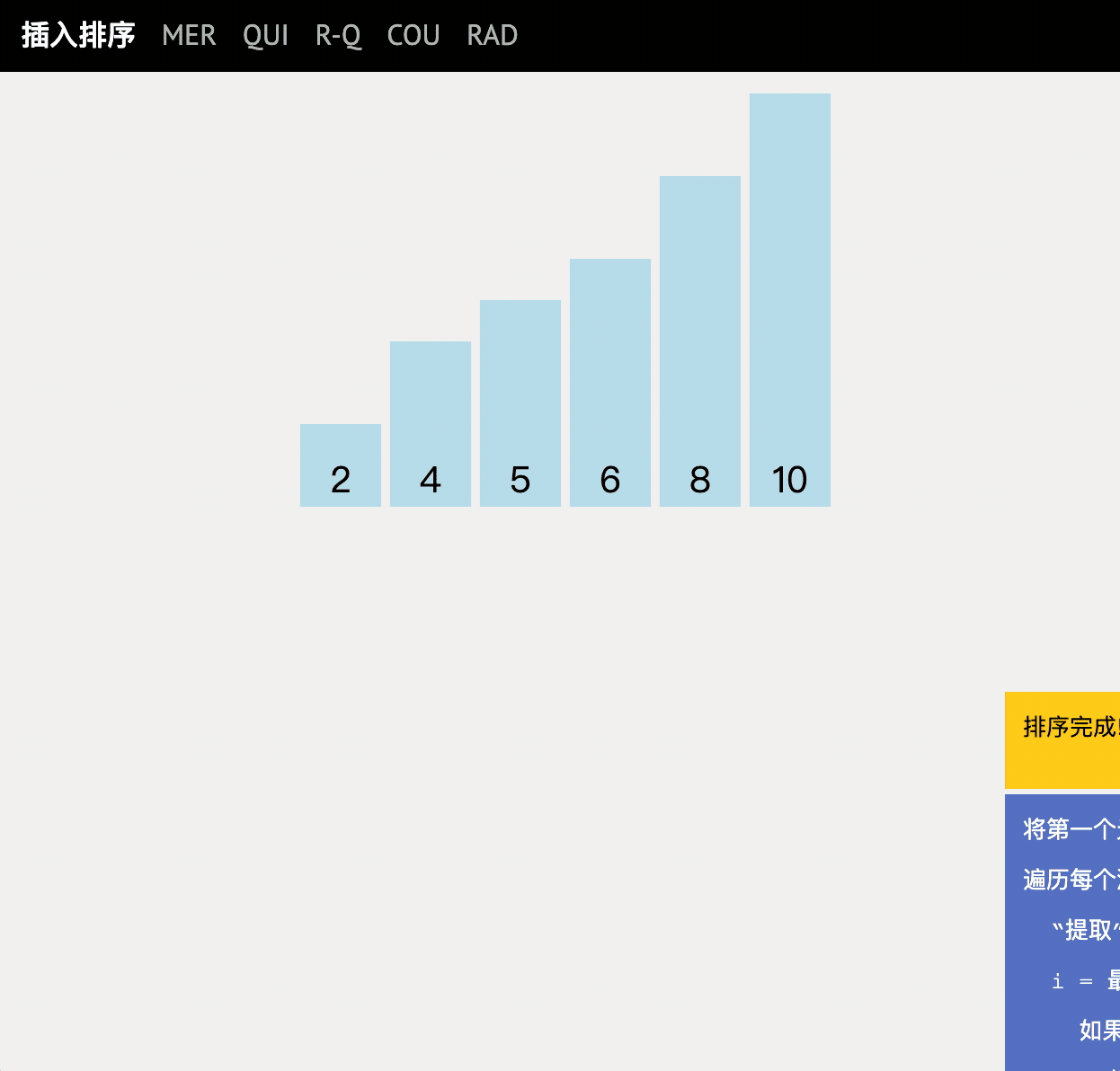
code implementation
/**
* Insert sort
* Author: One
* Date: 2021/09/23
*/
public class InsertSort {
public static void sort(int[] array) {
for (int i = 1; i < array.length; i++) {
//Insert an ordered sequence and expand the ordered sequence
for (int j = i; j > 0; j--) {
if (array[j]>array[j-1]){
int temp=array[j];
array[j]=array[j-1];
array[j-1]=temp;
}
}
// System.out.println(Arrays.toString(array));
}
}
}
Output results
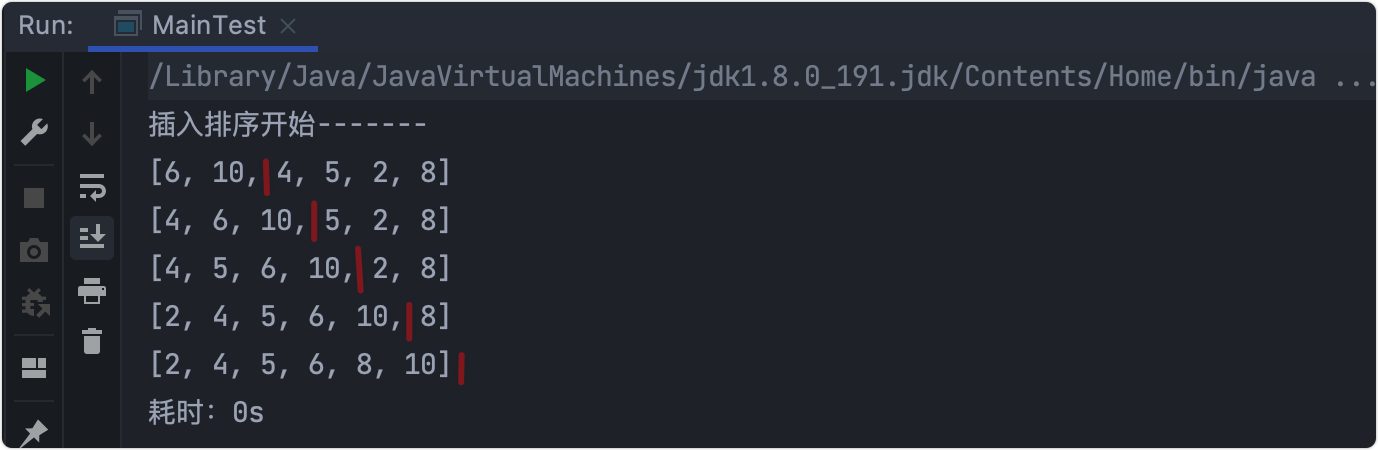
Time consuming test
Algorithm optimization
See Hill sorting below, which is Hill's optimization of insertion sorting.
Shell Sort
Hill sorting is an optimization of insertion sorting. When thinking about inserting 1 into [2,3,4,5,6], you need to move the positions of all elements once, that is, in some extreme cases, the efficiency is not high, also known as the algorithm is unstable.
Hill sort is an improved version of insert sort, also known as reduced incremental sort.
basic thought
Hill sort is to group records by a certain increment of subscript, and insert sort is used for each group;
As the increment decreases, each group contains more and more keywords. When the increment decreases to 1, the whole sequence is just divided into one group, and the algorithm terminates.
Like insertion sort, Hill sort is local and then local from local to all.
Dynamic diagram explanation
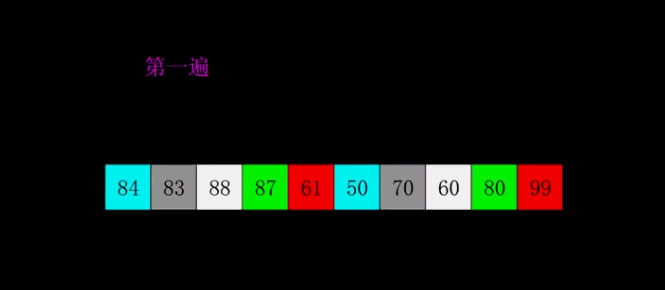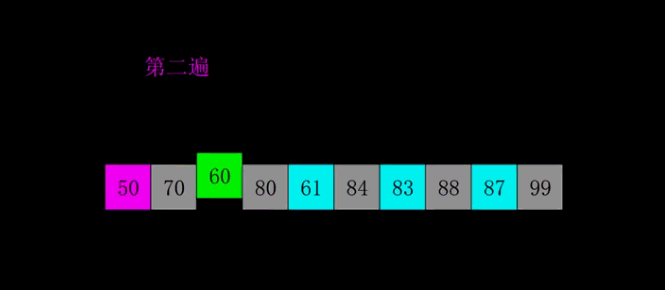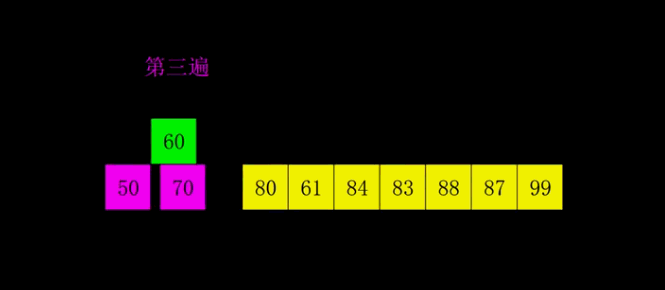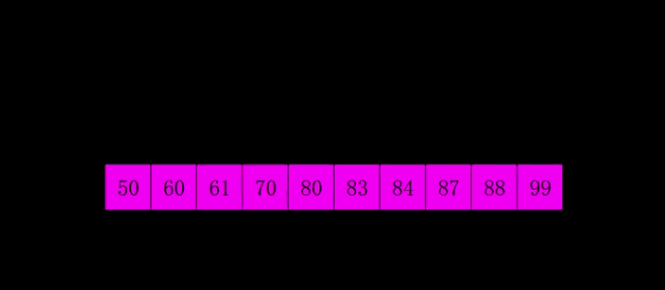
code implementation
/**
* Shell Sort
* Author: One
* Date: 2021/09/23
*/
public class ShellSort {
public static void sort(int[] array) {
System.out.println("Hill sort start--------");
//Gap initial increment = length/2 gradually reduced: gap/2
for (int gap = array.length/2; gap > 0 ; gap/=2) {
//Insert sort exchange method
for (int i = gap; i < array.length ; i++) {
int j = i;
while(j-gap>=0 && array[j]<array[j-gap]){
//The insertion sort adopts the exchange method
int temp = array[j];
array[j]=array[j-gap];
array[j-gap]=temp;
j-=gap;
}
}
System.out.println(Arrays.toString(array));
}
}
}
Output results
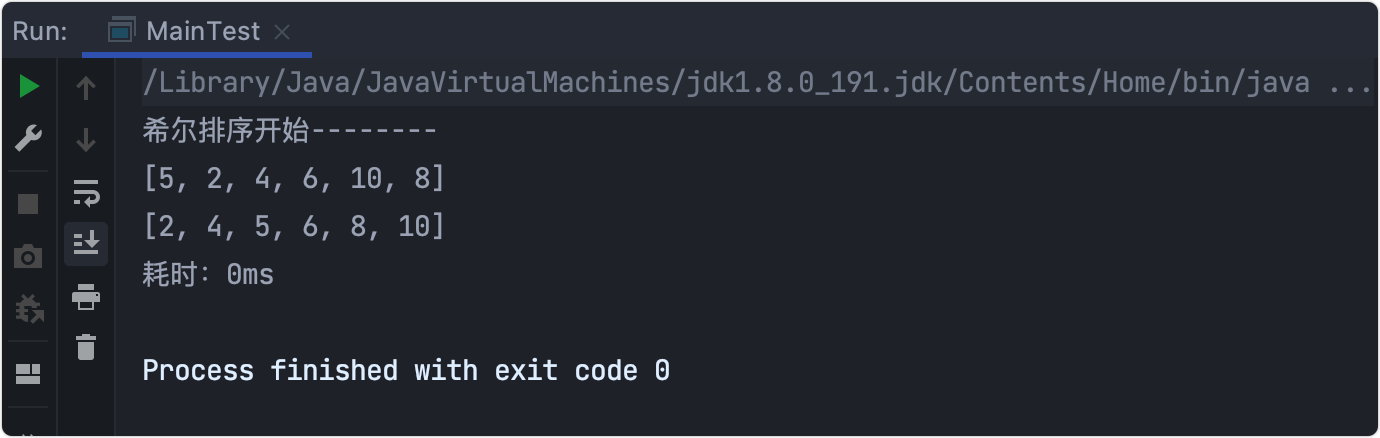
Time consuming test
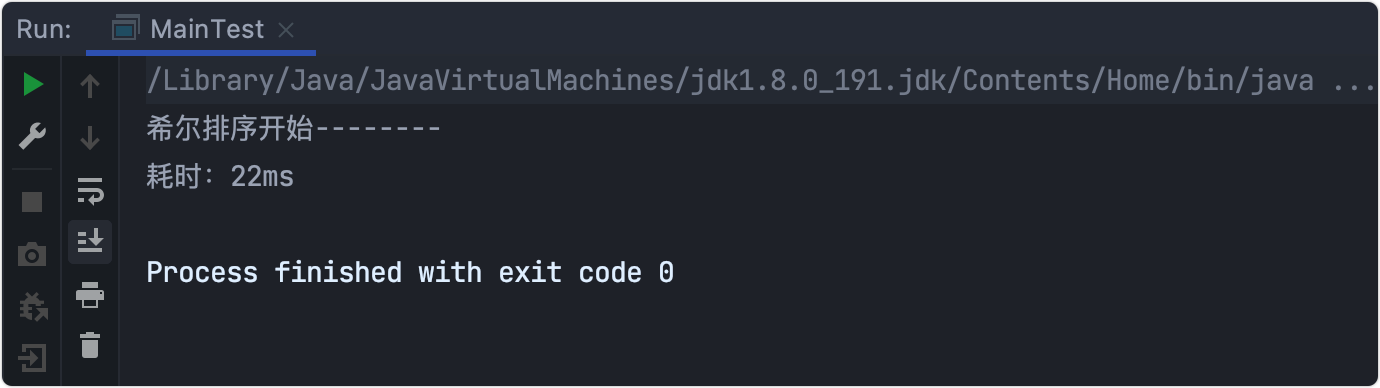
Algorithm optimization
nothing
Quick sort
Quicksort is an improvement of bubble sort. Compared with bubble sort, each exchange is jump.
basic thought
Divide the data to be sorted into two independent parts. All the data in one part is smaller than all the data in the other part. Then quickly sort the two parts of data according to this method. The whole sorting process can be recursive, so that the whole data becomes an ordered sequence.
It embodies the idea of divided governance.
Dynamic diagram explanation
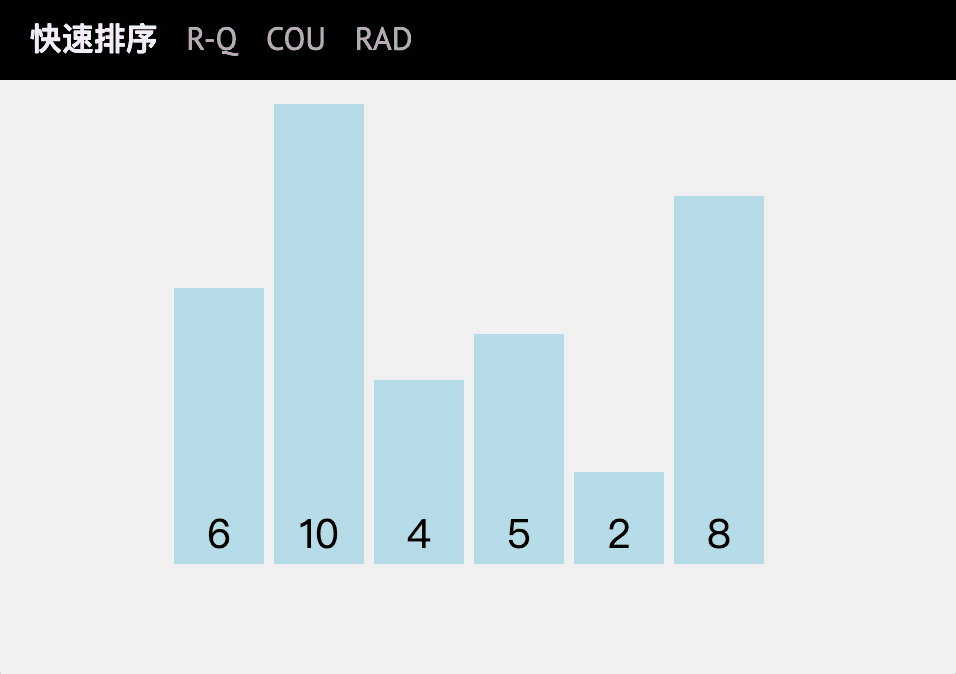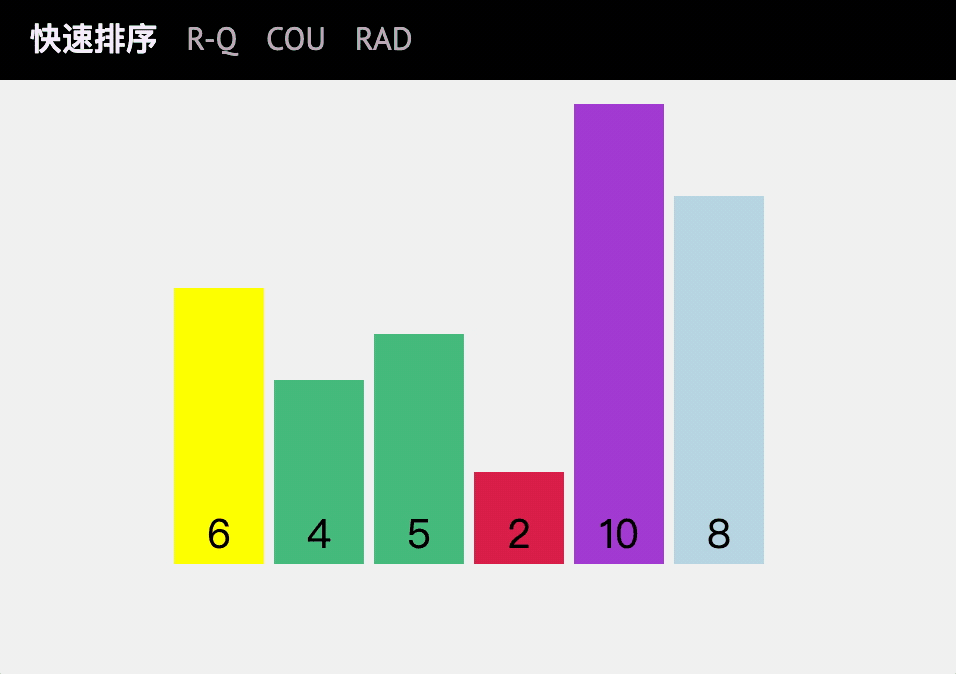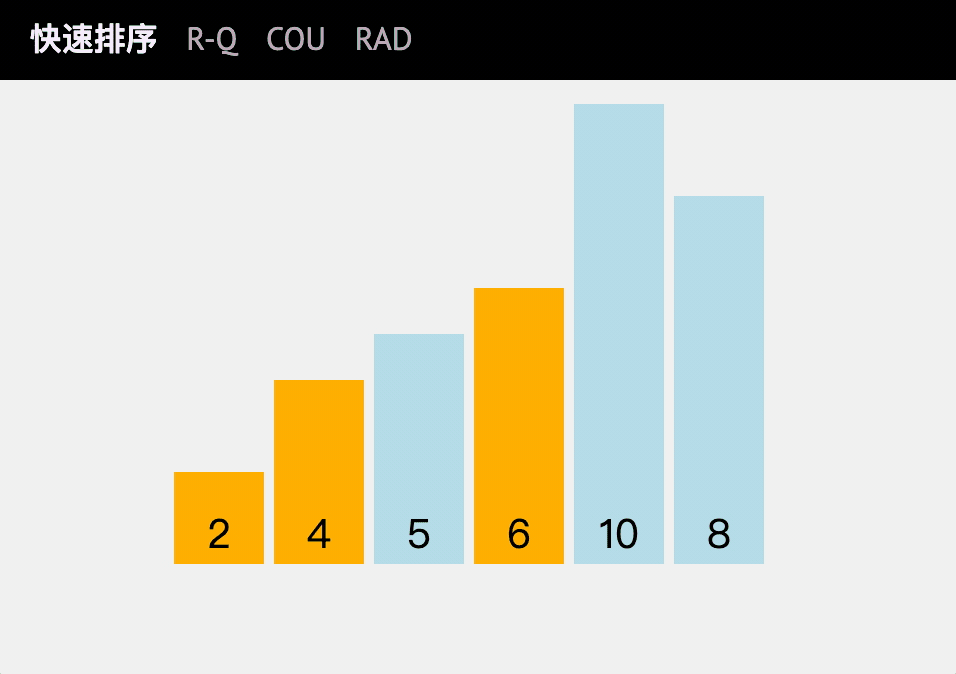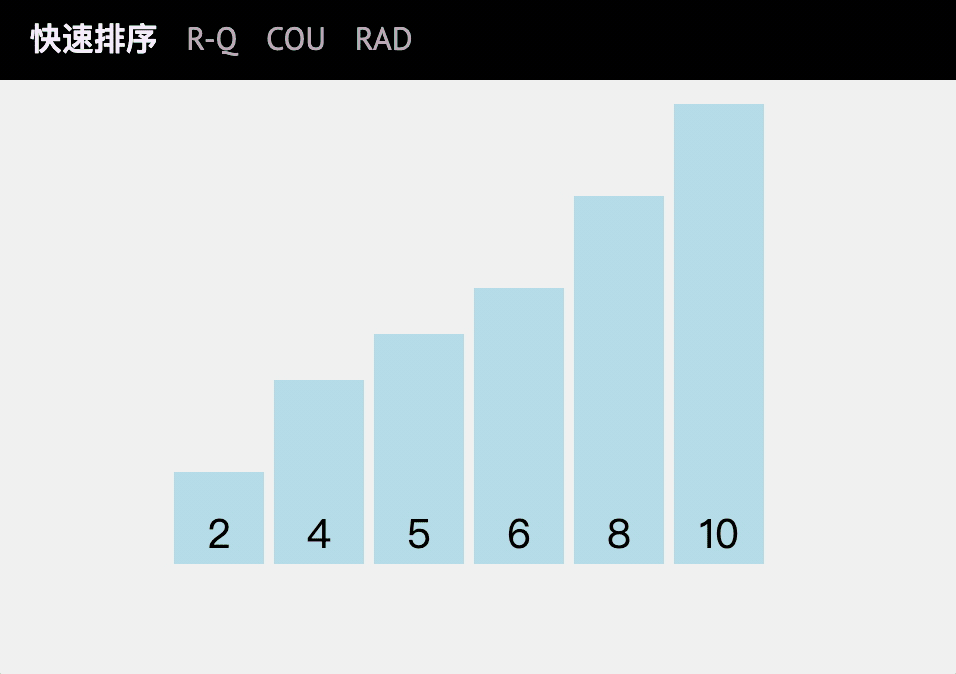
code implementation
The idea is as follows:
- First, find a number in this sequence as the reference number. For convenience, you can take the first number.
- Traverse the array, and place those less than the benchmark on the left and those greater than the benchmark on the right. Double pointers can be used here.
- At this time, the benchmark value divides the array into two halves, and the benchmark value is returned (find the sorted position).
- Using recursive algorithm, sort the sub arrays after divide and conquer.
public class QuickSort {
public static void sort(int[] array) {
System.out.println("Quick sort start---------");
mainSort(array, 0, array.length - 1);
}
private static void mainSort(int[] array, int left, int right) {
if(left > right) {
return;
}
//Double pointer
int i=left;
int j=right;
//Base is the base number
int base = array[left];
//The left is less than the datum and the right is greater than the datum
while (i<j) {
//First look to the right and decrease to the left
while (base<=array[j]&&i<j) {
j--;
}
//Look at the left and increase to the right
while (base>=array[i]&&i<j) {
i++;
}
//exchange
int temp = array[j];
array[j] = array[i];
array[i] = temp;
}
//Finally, the reference is the digital exchange equal to i and j
array[left] = array[i];
array[i] = base;
System.out.println(Arrays.toString(array));
//Recursive call to left half array
mainSort(array, left, j-1);
//Recursive call to right half array
mainSort(array, j+1, right);
}
}
Output results
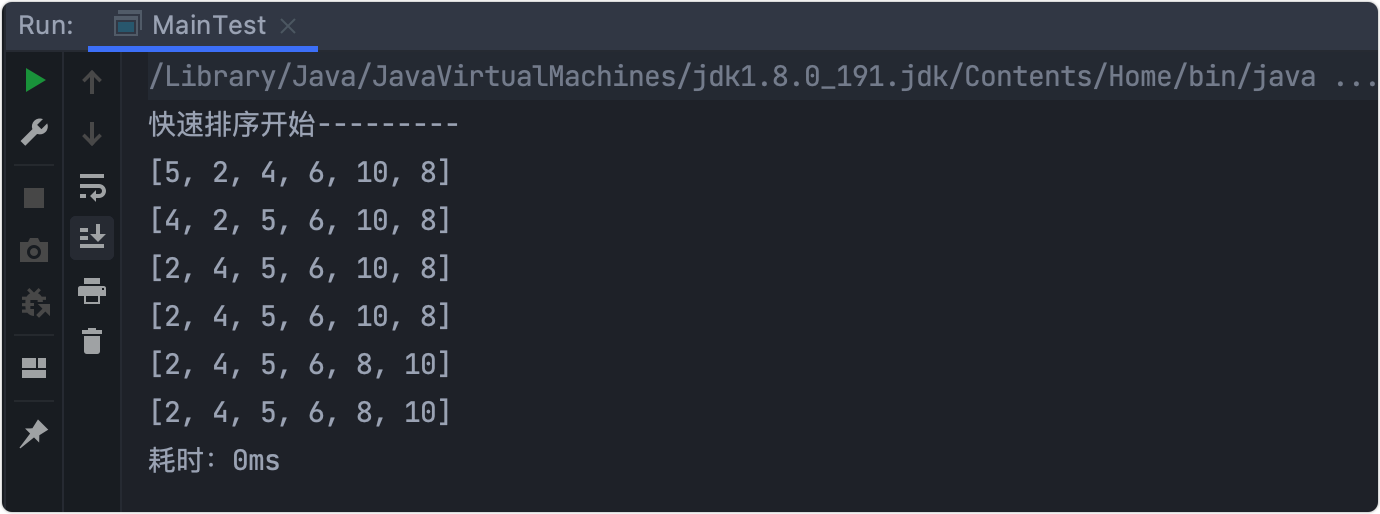
Stepwise analysis
- Take 6 as the reference number and use the left and right pointers to make the number on the left < 6 and the number on the right > 6.
- Recursion on the left and right sides, that is, use 5 as the benchmark on the left to continue the comparison.
- Until left > right ends the recursion.
Time consuming test
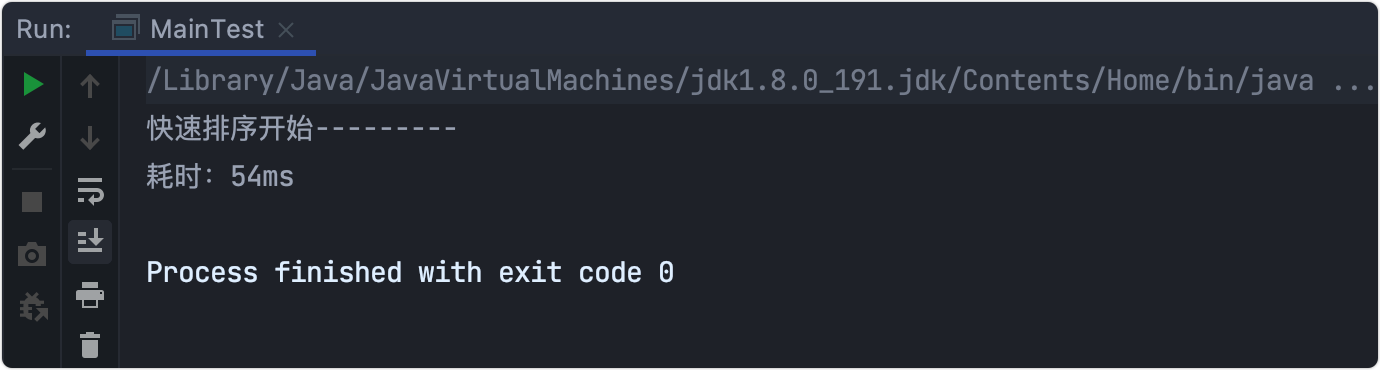
Why is quick sort so fast?
Algorithm optimization
Optimization one
Median of three: at present, we take the first number as the benchmark number. For some ordered sequences, cycles will be wasted, which can be optimized by the median of three. Perceptual partners can understand it by themselves.
Optimization II
Quick sort is very fast for long sequences, but it is not as good as insert sort for short sequences. It can be used comprehensively.
Heap sort
This chapter has high requirements for basic knowledge, which can be skipped by beginners.
basic thought
Heap sort is a sort algorithm designed by using the data structure of heap. Heap sort is a * * selective sort, * * its worst, best, average time complexity is O(nlogn), and it is also an unstable sort. First, simply understand the lower heap structure.
heap
Heap is a complete binary tree with the following properties:
- The value of each node is greater than or equal to the value of its left and right child nodes, which is called large top heap;
- The value of each node is less than or equal to the value of its left and right child nodes, which is called small top heap.
It mainly uses the maximum or minimum characteristics of heap top elements to realize sorting by continuously constructing large top heap, exchanging heap top and tail, and broken tail reconstruction.
Dynamic diagram explanation

code implementation
public class HeapSort {
public static void sort(int[] array) {
//Create heap
for (int i = (array.length - 1) / 2; i >= 0; i--) {
//Adjust the structure from the first non leaf node from bottom to top and from right to left
adjustHeap(array, i, array.length);
}
//Adjust heap structure + exchange top and end elements
for (int i = array.length - 1; i > 0; i--) {
//Swap top and end elements
int temp = array[i];
array[i] = array[0];
array[0] = temp;
//Readjust the heap
adjustHeap(array, 0, i);
}
}
/**
* Adjustment reactor
* @param array Waiting sequence
* @param parent Parent node
* @param length Index of the last element of the sequence to be sorted
*/
private static void adjustHeap(int[] array, int parent, int length) {
//temp as parent node
int temp = array[parent];
//Left child
int lChild = 2 * parent + 1;
while (lChild < length) {
//Right child
int rChild = lChild + 1;
// If there is a right child node and the value of the right child node is greater than the left child node, the right child node is selected
if (rChild < length && array[lChild] < array[rChild]) {
lChild++;
}
// If the value of the parent node is already greater than the value of the child node, it ends directly
if (temp >= array[lChild]) {
break;
}
// Assign the value of the child node to the parent node
array[parent] = array[lChild];
//Select the left child node of the child node and continue to filter down
parent = lChild;
lChild = 2 * lChild + 1;
}
array[parent] = temp;
System.out.println(Arrays.toString(array));
}
}
Output results
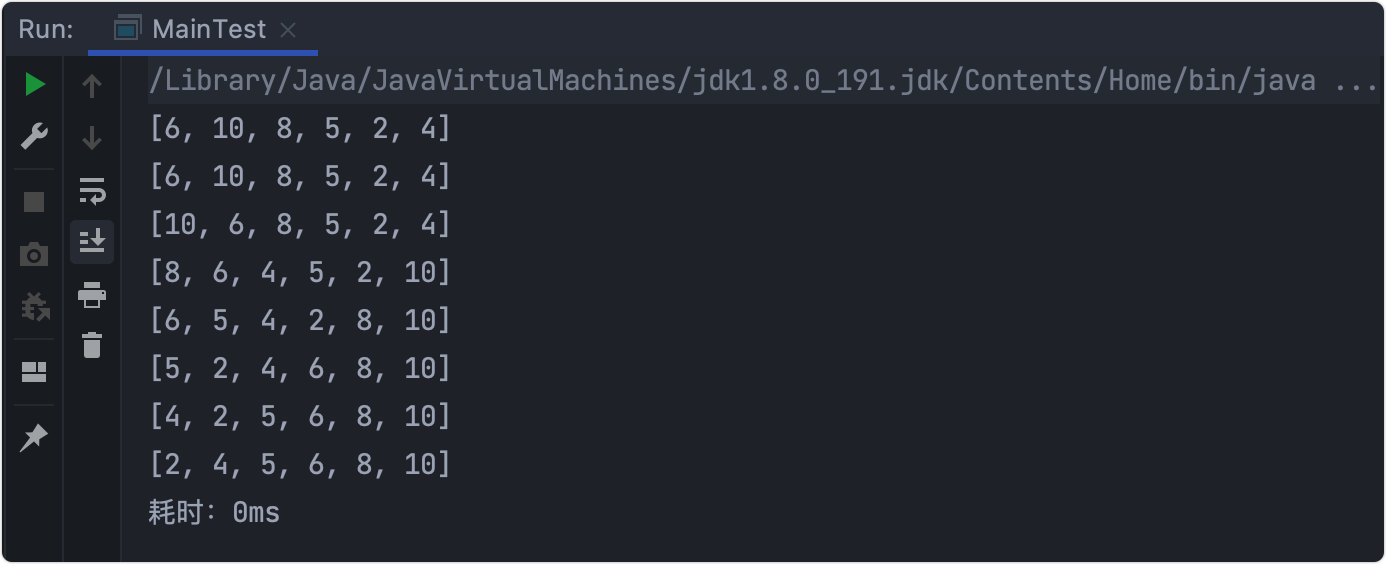
Stepwise analysis
- Build the initial heap, and form the sequence to be arranged into a large top heap (or small top heap), ascending large top heap and descending small top heap;
- Swap the heap top element with the heap tail element, and disconnect (remove) the heap tail element.
- Rebuild the heap.
- Repeat 2 ~ 3 until there is only one element (heap top element) left in the sequence to be arranged.
Time consuming test
Algorithm optimization
The key to the optimization point is how we find the position of the top element. Interested students can continue to study.
Merge sort
basic thought
Merge sort is a sort method based on the idea of merge, which adopts the classical divide and conquer strategy.
The disordered sequence is continuously divided into half, arranged in order and then spelled back, which is realized by recursion.
The difficulty is how to merge two ordered arrays?
We can open up a temporary array and use fast and slow pointers to assist our merging.
Although additional space is required to complete this sort. But now the memory of computers is relatively large, and the efficiency of time is much more important than that of space.
Therefore, space for time is also a direction of optimization algorithm.
Dynamic diagram explanation
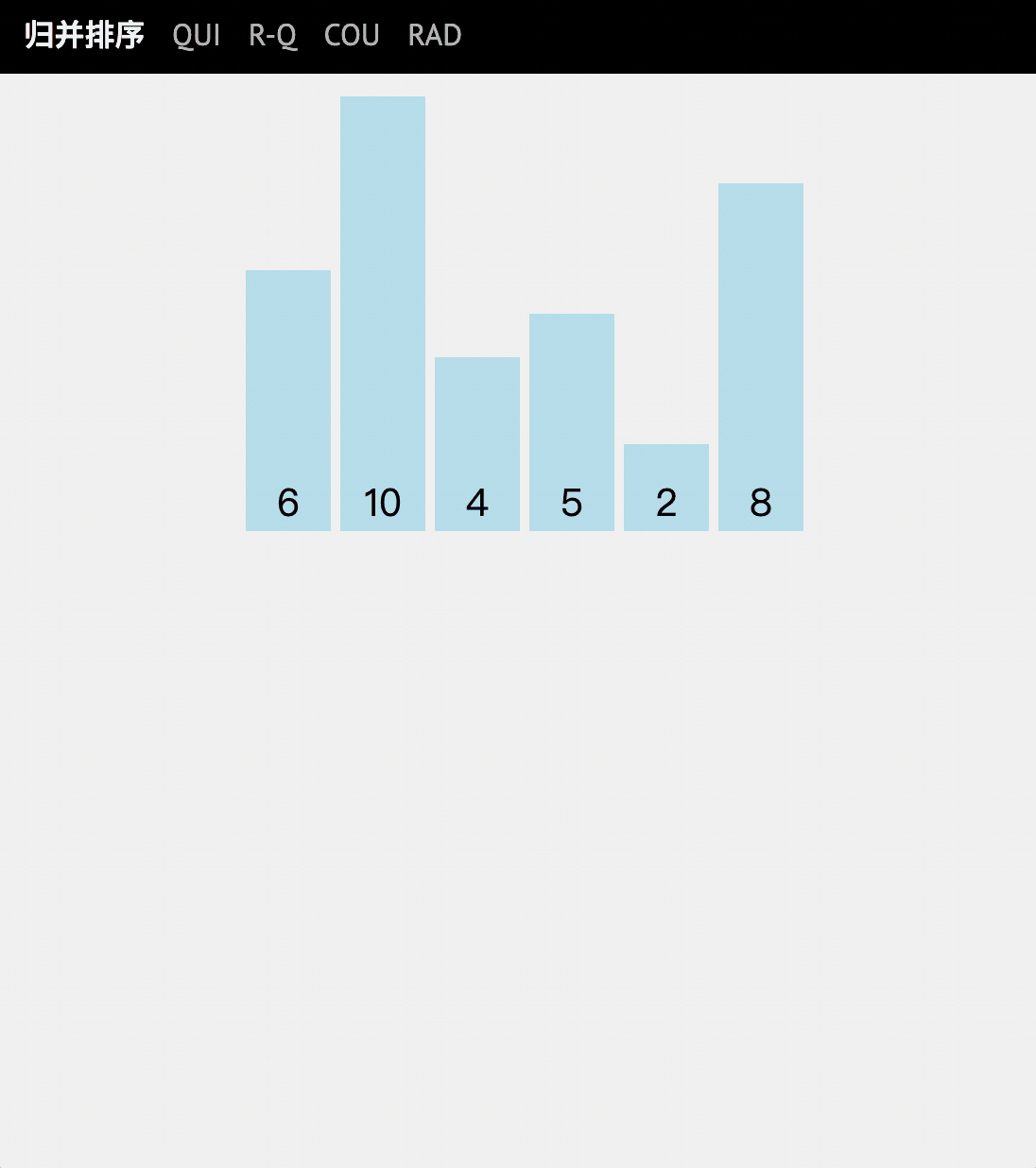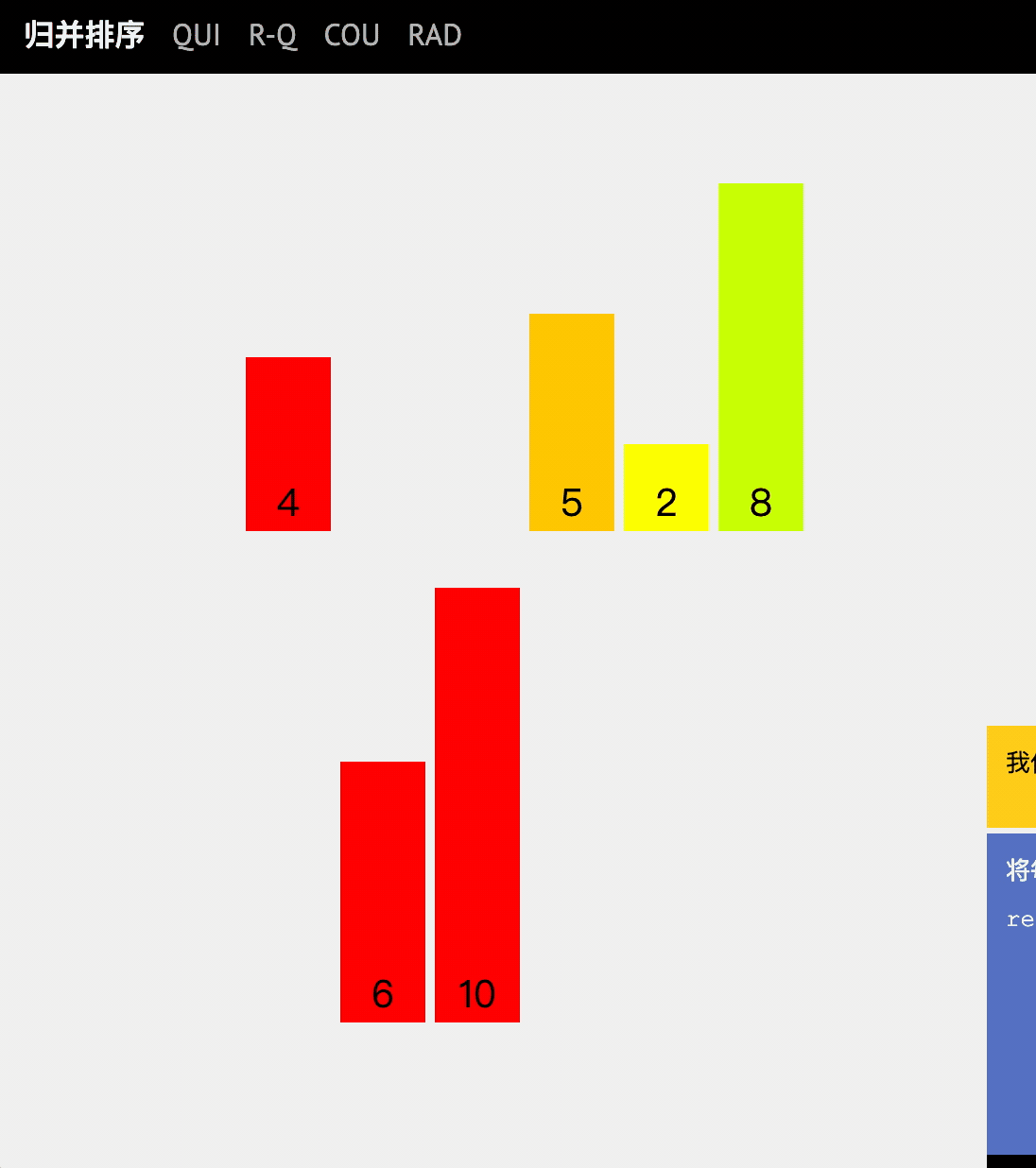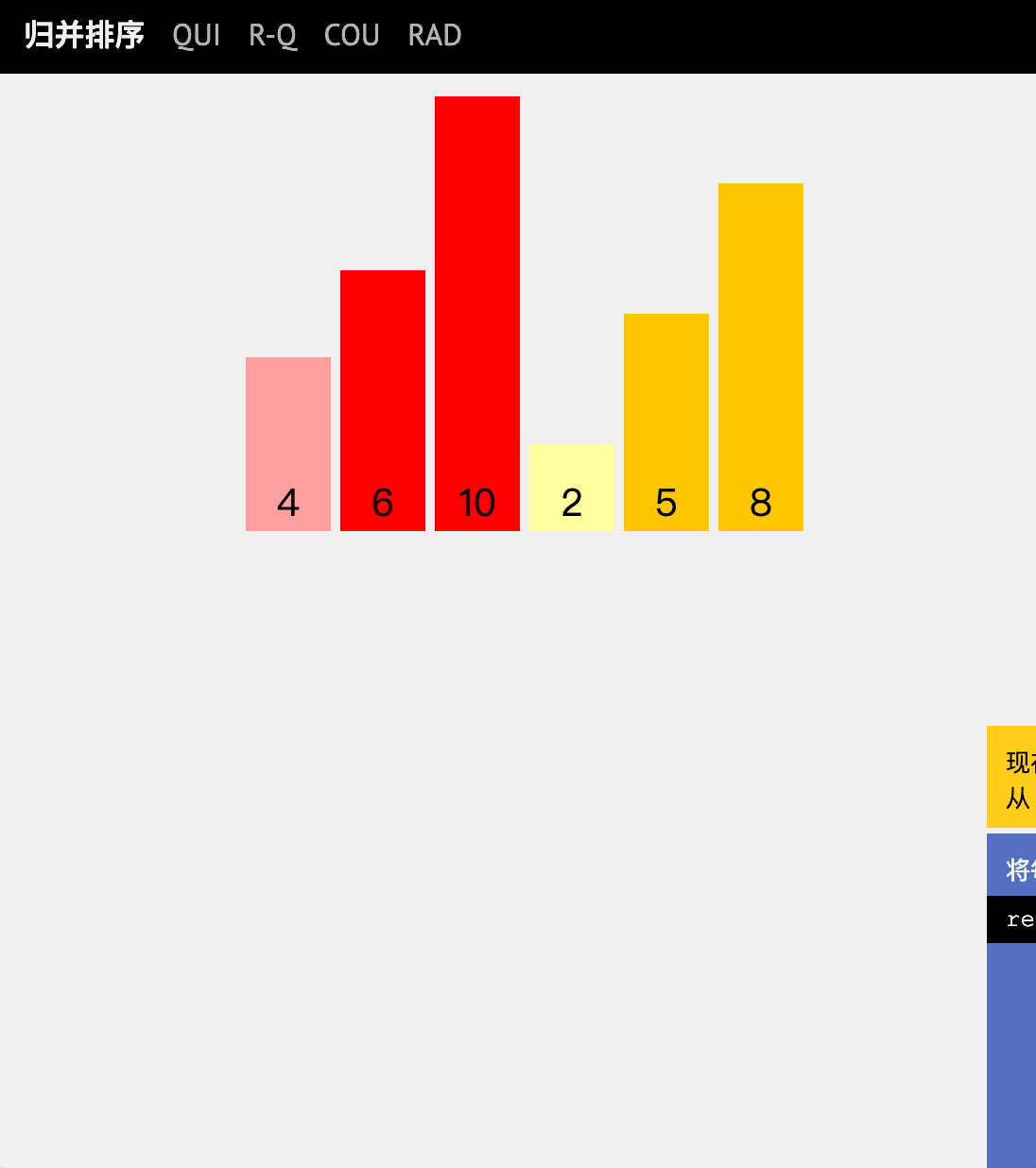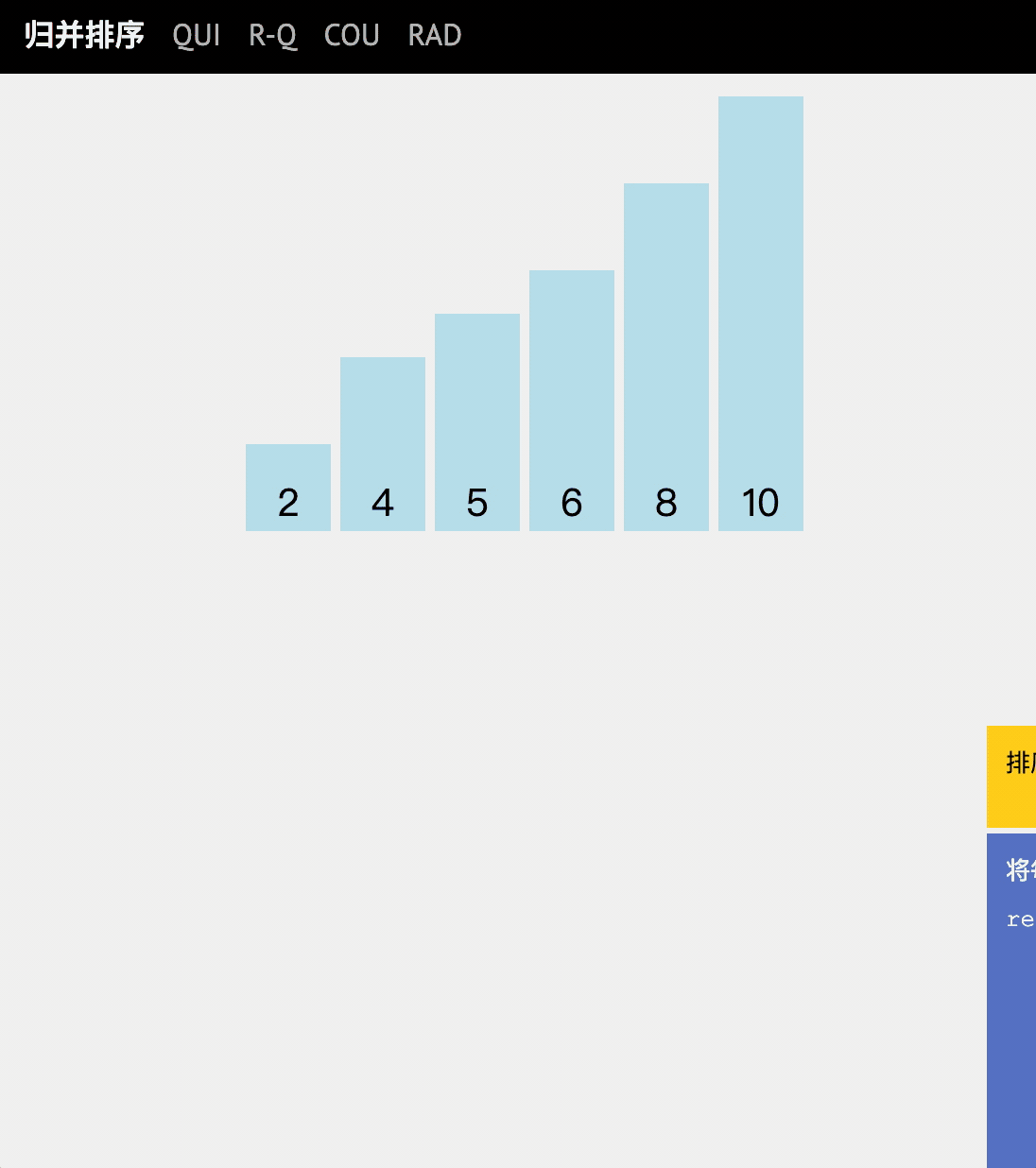
code implementation
public class MergeSort {
public static void sort(int[] array){
divide(array,0,array.length-1);
}
private static int[] divide(int[] array, int left, int right) {
int mid = (left+right)/2;
if(left<right){
divide(array,left,mid);
divide(array,mid+1,right);
//Left and right merging
merge(array,left,mid,right);
}
System.out.println(Arrays.toString(array));
return array;
}
public static void merge(int[] array, int left, int mid, int right) {
int[] temp = new int[right-left+1];
int i= left;
int j = mid+1;
int k=0;
// Move the smaller number to the new array first
while(i<=mid && j<=right){
if(array[i]<array[j]){
temp[k++] = array[i++];
}else{
temp[k++] = array[j++];
}
}
// Move the remaining number on the left into the array
while(i<=mid){
temp[k++] = array[i++];
}
// Move the remaining number on the right side into the array
while(j<=right){
temp[k++] = array[j++];
}
// Overwrite the num array with the number in the new array
for(int x=0;x<temp.length;x++){
array[x+left] = temp[x];
}
}
}
Output results
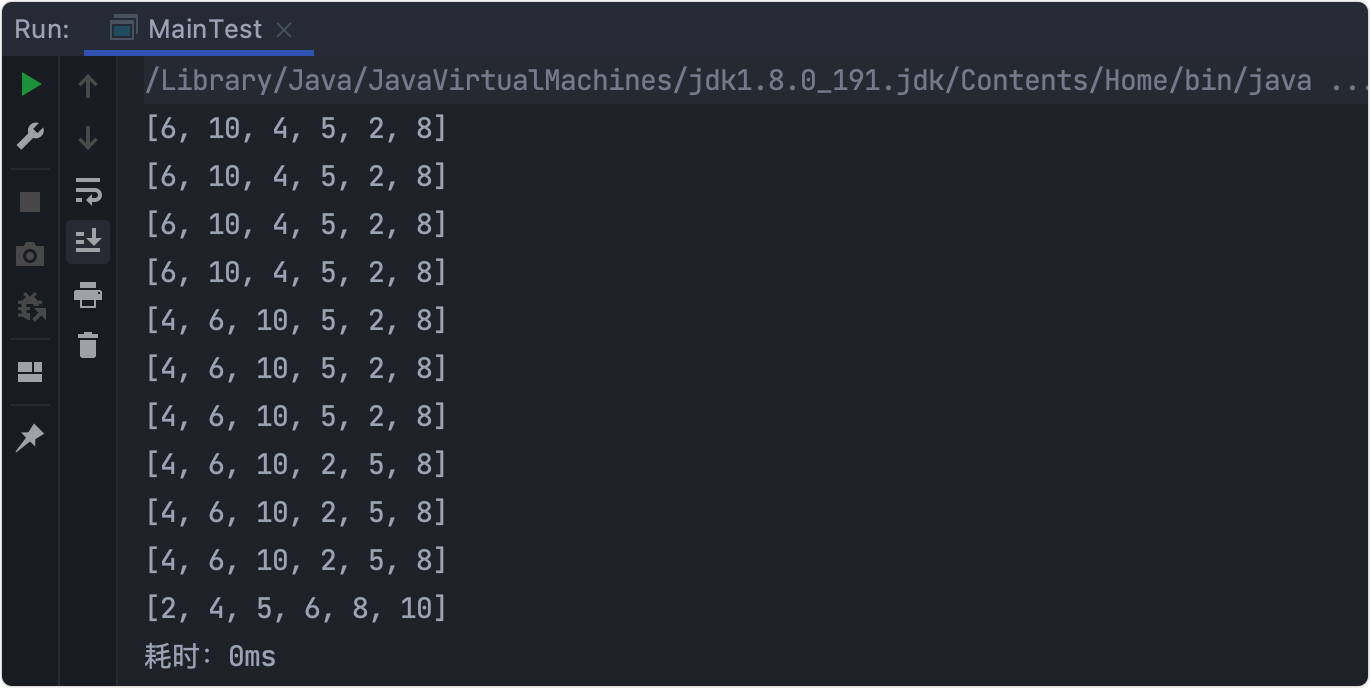
Time consuming test
Algorithm optimization
Count sort
From here on, it is non comparative sorting.
basic thought
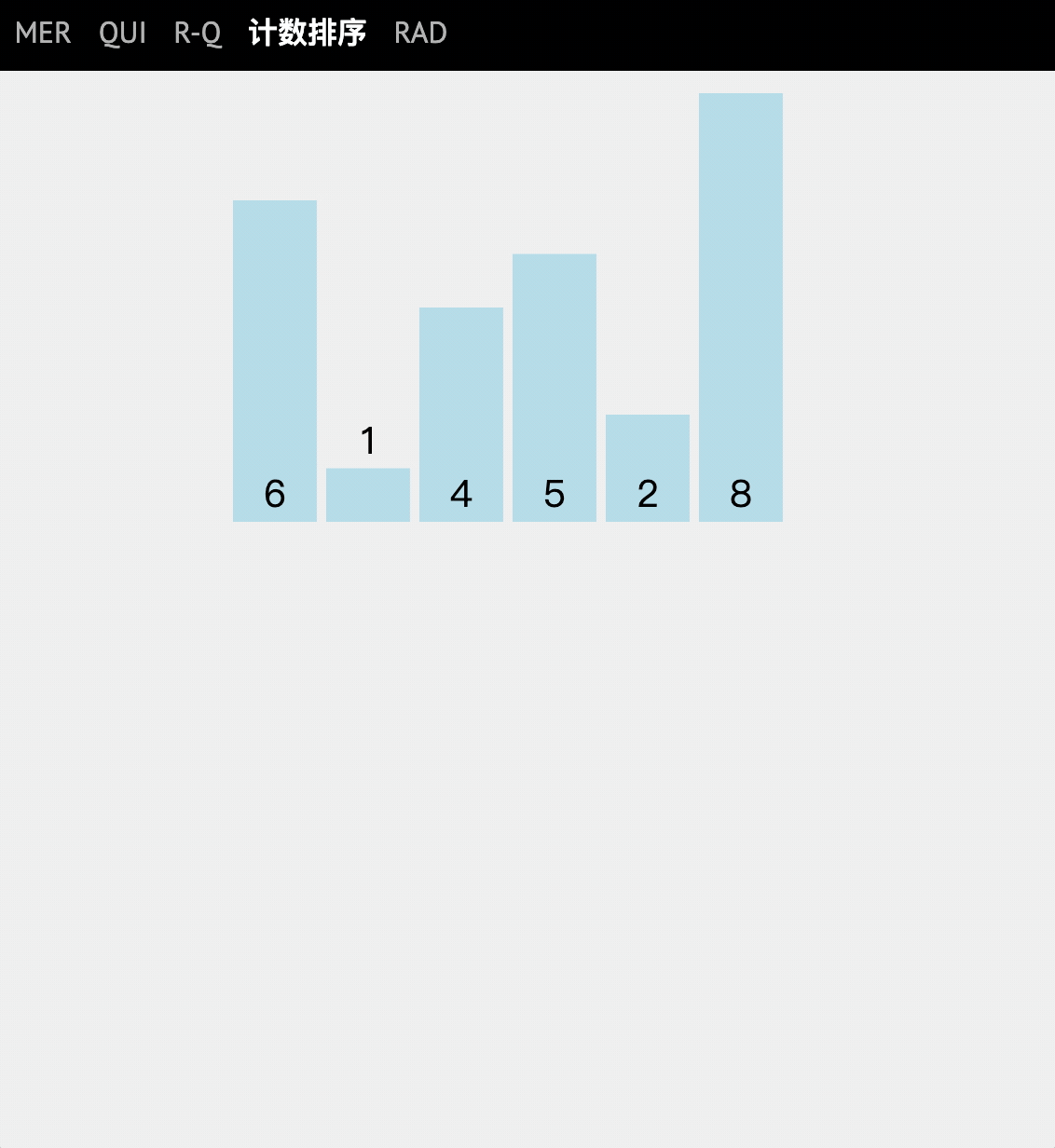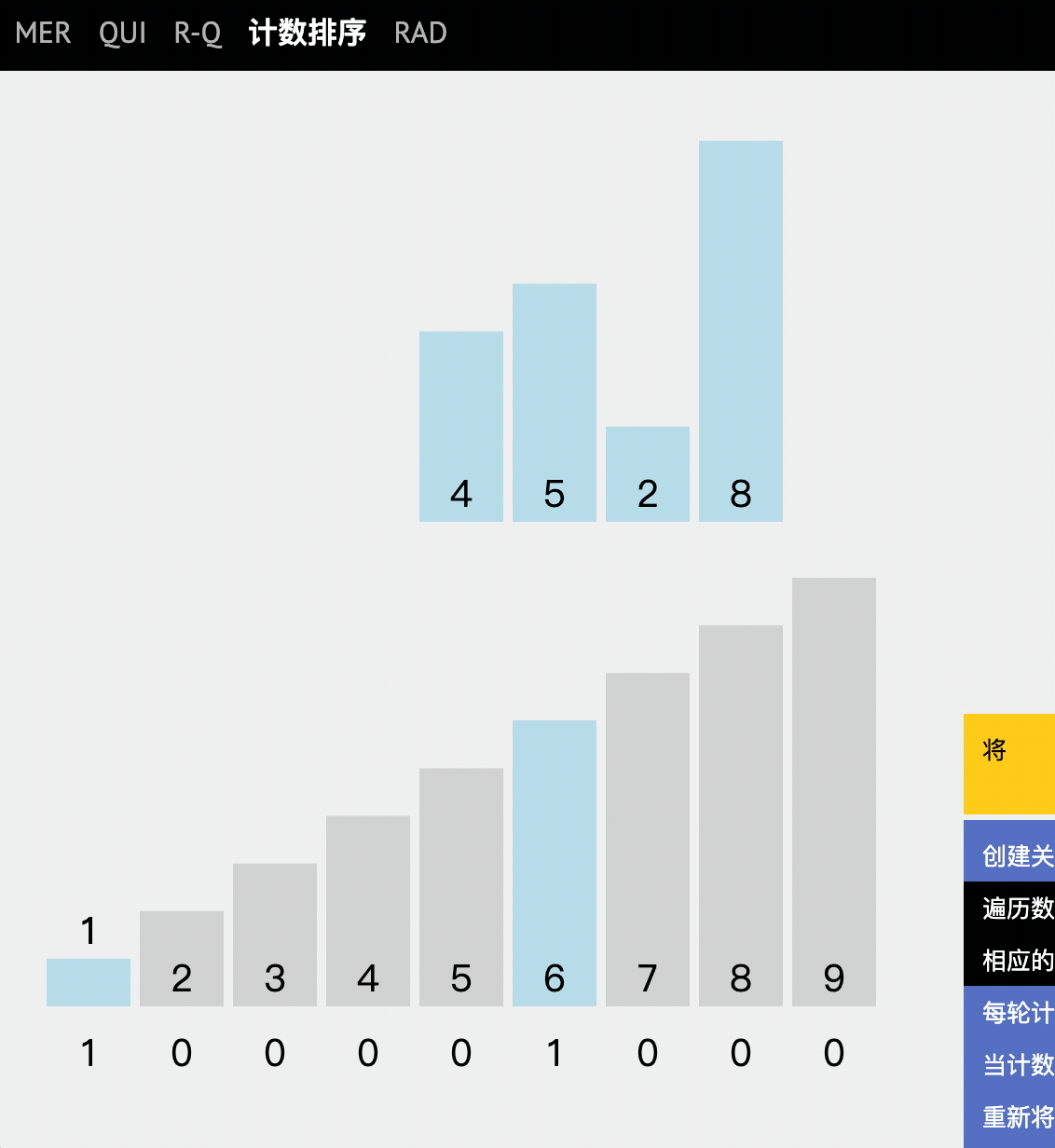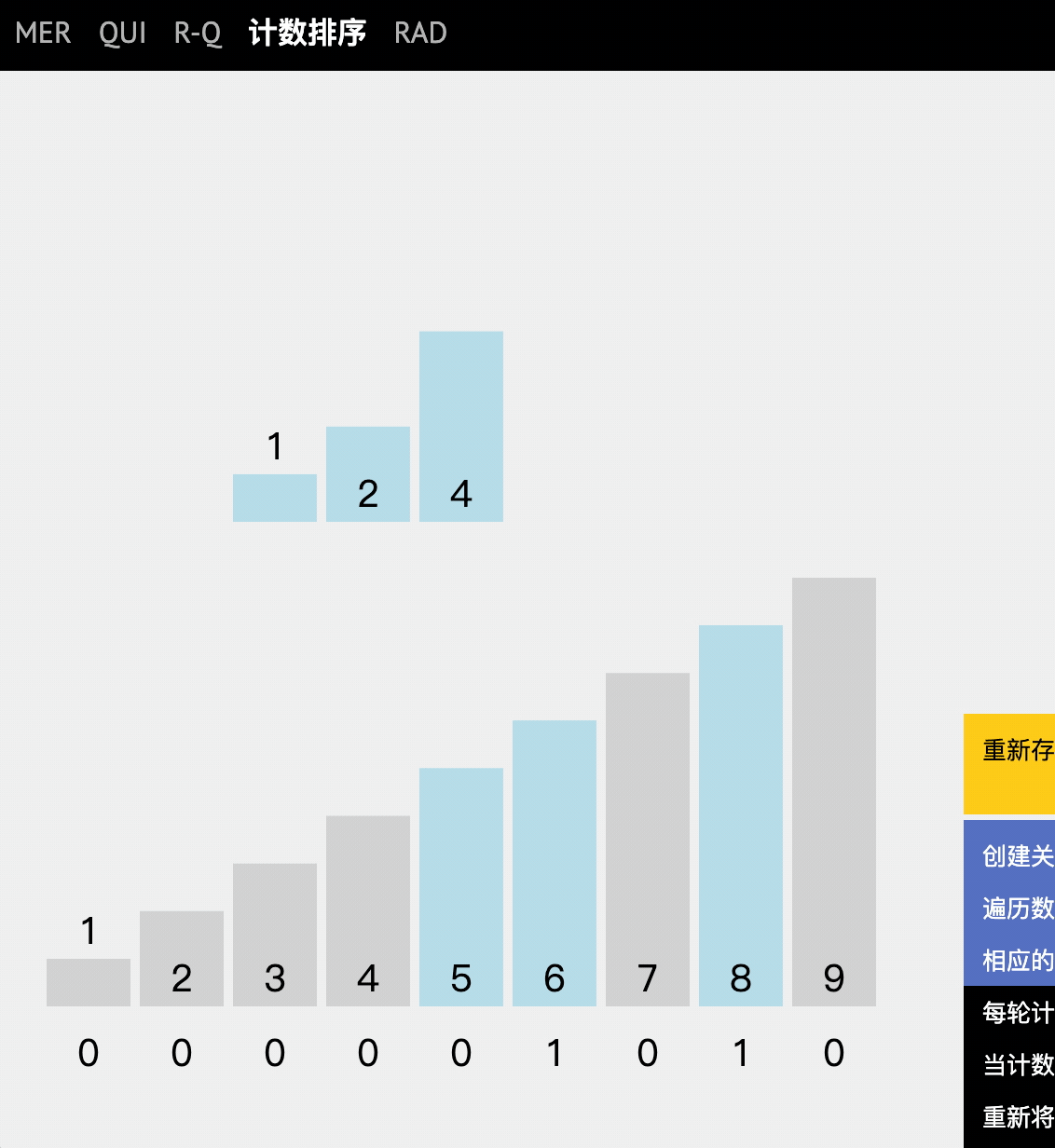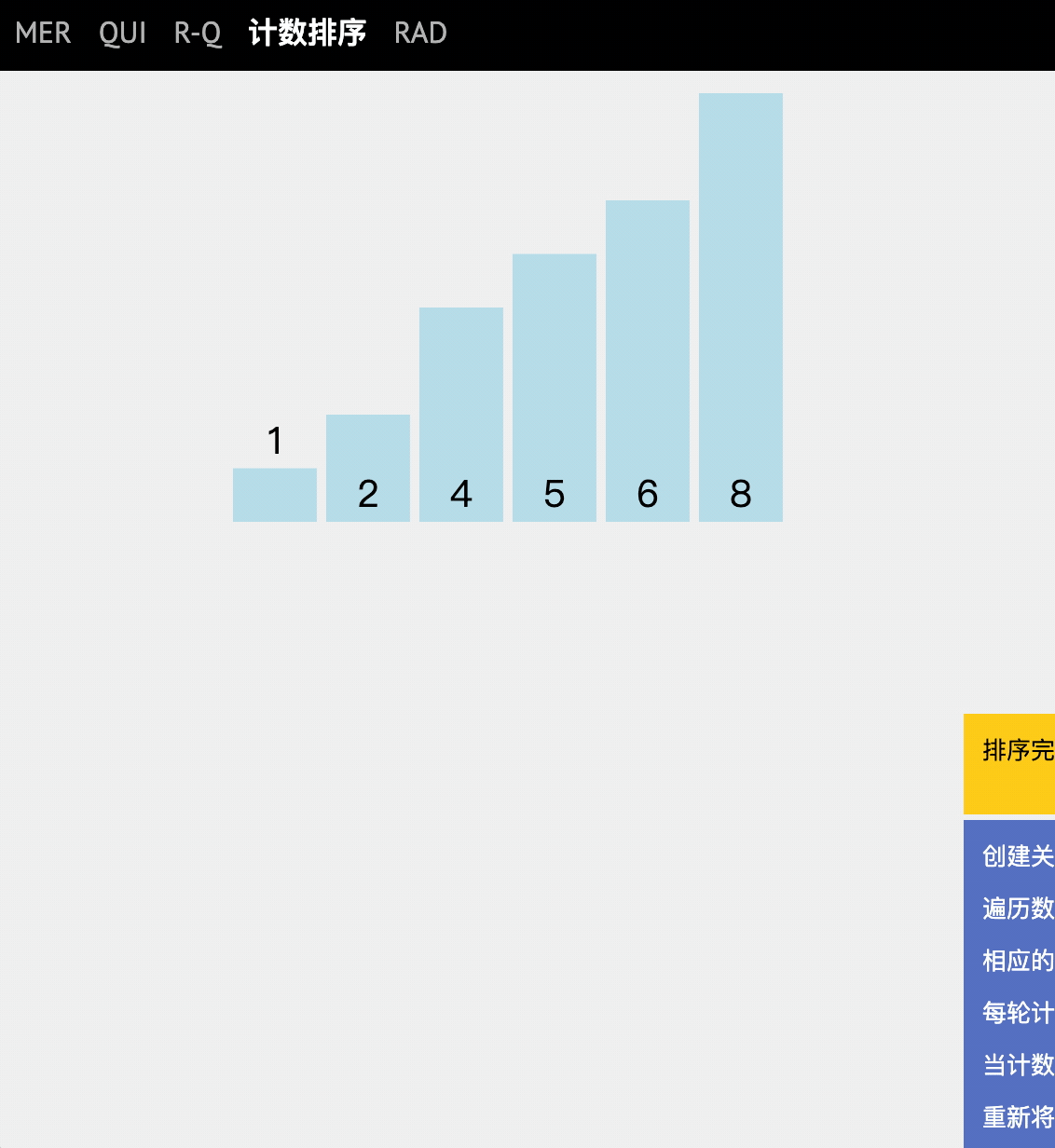
If we input a number x, if we can find several numbers smaller than this number, then we can directly put x into the position of the corresponding output array.
For example, if x=5 in the test sequence and there are 2 smaller than 5, there is no doubt that 5 should be ranked third.
Dynamic diagram explanation
code implementation
public class CountSort {
public static void sort(int[] array) {
System.out.println("Count sort start--------");
//Calculate the maximum and minimum values to determine the length of count []
int max = array[0], min = array[0];
for (int i : array) {
if (i > max) {
max = i;
}
if (i < min) {
min = i;
}
}
//count [] is used to store the number of occurrences of each element
int[] count = new int[max - min + 1];
//Statistical frequency
for (int i : array) {
count[i - min] += 1;//Number position + 1
}
//Create the final returned array with the same length as the original array, but the sorting is completed
int[] result = new int[array.length];
int index = 0;//Record the subscript of the final array
//First loop each element in the subscript of the count sorter
for (int i = 0; i < count.length; i++) {
//The number of times the traversal loop occurs
for (int j = 0; j < count[i]; j++) {//count[i]: the frequency of this number
result[index++] = i + min;//It was thought that min was reduced, and now add min, the value becomes the original value
}
System.out.println(Arrays.toString(result));
}
}
}
Output results
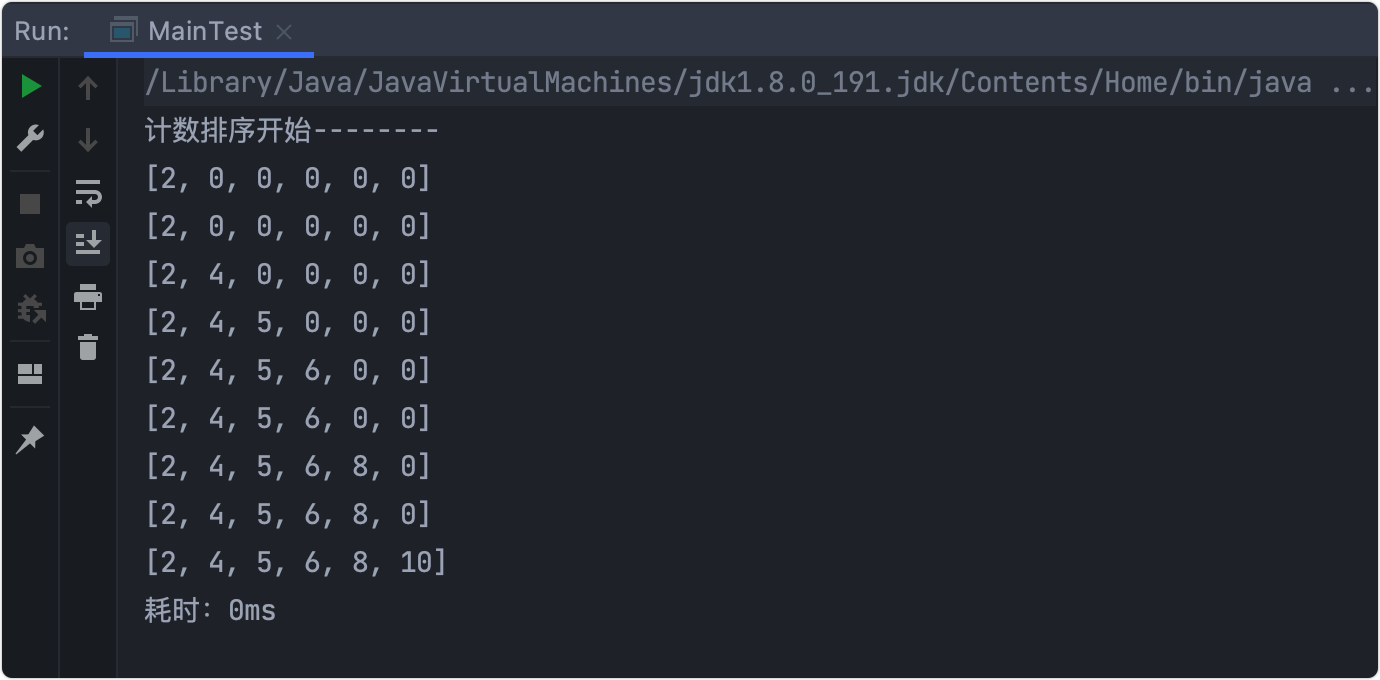
Stepwise analysis
- Is to record the frequency (number of times) of the values in the original array in the subscript of the new array.
- Traverse the number of occurrences and put them into the new array in turn.
Time consuming test
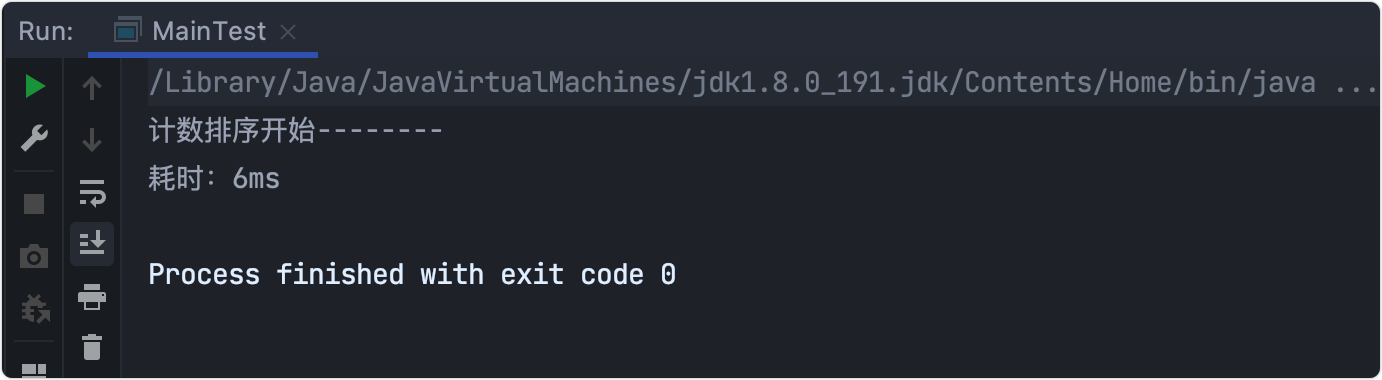
To tell you the truth, this speed surprised me. The time complexity of counting sorting is O(n), but the disadvantage is to limit the integer range to [0,k].
Algorithm optimization
The normal count sorting starts from 0. The code implemented in this paper starts from min and has been optimized.
summary
This article does not specifically introduce the time complexity, because I put a number here, you simply can't understand their gap.
Test the eight sorting algorithms with an array of 100000 length, and turn abstraction into concrete. When there is a large amount of data, the advantage of nlogn will be greater and greater than n^2. When n=10^5, the nlogn algorithm is 6000 times faster than the n^2 algorithm. What is the concept? If we want to process a data set, the nlogn algorithm will process it for one day, and the n^2 algorithm will process it for 6020 days. This is basically equivalent to 15 years.
An optimized and improved algorithm may be much faster than a stupid algorithm, which is the reason why big factories examine the algorithm and we learn the algorithm.
As the old saying goes: take advantage of the wisdom of all, and you will be free; With the power of everyone, nothing is invincible. In order to conquer the mountain of algorithm, I have formulated a team problem brushing plan, with at least one leetcode algorithm problem every day.
It's hard to give up.
If you are a freshman and keep studying every day, you will brush at least 1200 questions more than others, and your salary may be 3-4 times that of others when you graduate.
If you are a professional, you can improve yourself every day, get a raise and become a technical expert.
As long as you are willing to struggle and always walk on the road of struggle, your life, the worst result, is just a late success.
Click here Join the program
If the link is blocked or there is a permission problem, it can be solved by the private chat author.
Exclusive benefits for fans
📚 Java: 1.5G learning materials - reply to "materials"
📚 Algorithm: video book - reply to "algorithm"