queue
Basic concepts
- Queue is a first in first out (FIFO) data structure.
- For a queue, the end of the table is called the tail, and the end of the header is called the front.
- All elements can only enter from the end of the queue. The operation of entering the queue is called joining the queue.
- At the same time, all elements can only be ejected from the queue head. The operation of ejecting the queue is called out of the queue.
- Because operations can only be performed on the queue head or tail elements, random access to the elements in the queue is not supported, that is, we cannot access the elements in the queue at any position, but only from the queue head or tail.
Picture demonstration of joining and leaving the team
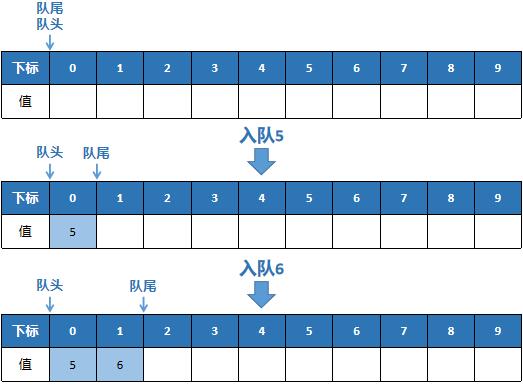
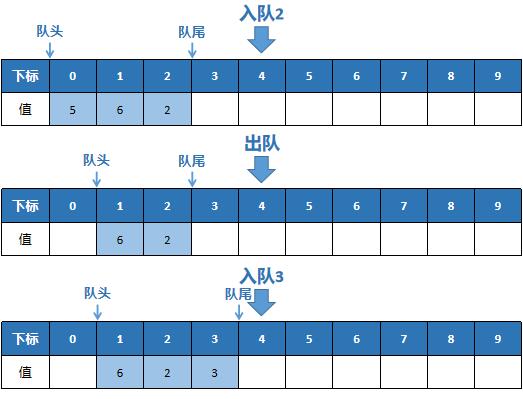
Basic operation of queue
- Team head (tail) pointer: the subscript pointing to the team head (tail). Note that the interval between the head and tail of the team is a left closed and right open interval.
- Queue entry: put the elements into the queue, and the end of the queue pointer + 1. Pay attention to judge whether the queue is full. If so, the queue needs to be expanded or prohibited from entering the queue.
- Out of queue: pop up the top element of the queue, and the queue head pointer + 1. Pay attention to judge whether the queue is empty. If the queue is empty and still out of the queue, an error will be reported.
- Judge whether the queue is empty: return yes or no.
- Calculate the number of elements in the queue: returns the number of elements in the queue.
Code example
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
//Custom queue structure
typedef struct my_queue
{
int front, tail;
int size;
int* data;
}my_queue;
//Initialize queue
my_queue* init_queue(int num)
{
my_queue* t = (my_queue*)malloc(sizeof(my_queue));
t -> front = 0;
t -> tail = 0;
t -> size = num;
t -> data = (int*)malloc(sizeof(int) * num);
return t;
}
//Queue operation
//Return value: 1 succeeded, 0 failed
int queue_push(my_queue* que, int num)
{
if(que -> tail == que -> size) return 0;
que -> data[que -> tail++] = num;
return 1;
}
//Out of line operation
int queue_pop(my_queue* que)
{
return que -> data[que -> front++];
}
//Judge that the queue is empty
//Return value: 1 true, 0 false
int queue_is_empty(my_queue* que)
{
if(que -> front == que -> tail) return 1;
return 0;
}
//Count the number of elements in the queue
int queue_size(my_queue* que)
{
return que -> tail - que -> front;
}
int main()
{
my_queue* que = init_queue(10);
//Queue operation test
srand(time(0));
int n;
printf("Please enter the number of tests:\n");
scanf("%d", &n);
for(int i = 0; i < n; i++)
{
int op = rand() % 3;
switch(op)
{
//Join the team
case 0:
{
if(queue_push(que, i))
printf("element %d Team success!\n", i);
else printf("Failed to join the team!\n");
break;
}
//Out of the team
case 1:
{
if(queue_is_empty(que)) break;
printf("The outgoing element is%d\n", queue_pop(que));
break;
}
//Number of read elements
case 2:
{
printf("The number of elements in the queue is:%d\n", queue_size(que));
break;
}
}
}
return 0;
}
Related topics
Circular queue
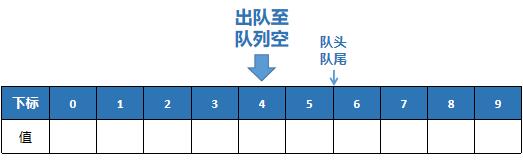
One day, Ben konjac used the queue to find that there was still a place to store elements in the queue, but at this time, we couldn't store elements. (as shown in the figure below)
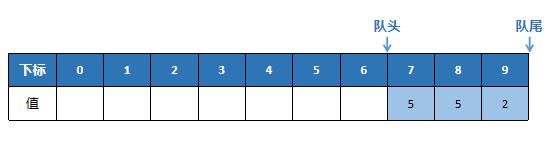
In this case, Ben konjaku said to eat a kilo: if we go on like this, isn't the utilization rate of my queue low? So after consulting the teacher, the teacher told me that it could be solved by circular queue.
Basic concepts
- Same concept as queue
Basic operation of circular queue
- Team head (tail) pointer: the subscript pointing to the team head (tail). Note: (1) the queue head and tail interval is a left closed and right open interval (2) when the queue is full, a solution to the conflict with the empty queue is that the queue tail pointer should be in the position before the queue head pointer (otherwise it will be difficult to distinguish whether the queue is empty or full), that is, (queue tail pointer + 1)% queue size = queue head pointer
- Queue entry: put the elements into the queue, and then model the queue size after the end of the queue pointer + 1 (pay attention to the number of non elements). Pay attention to judge whether the queue is full. If so, you need to expand the queue or prohibit entering the queue.
- Out of queue: pop up the top element of the queue. At the same time, the queue head pointer + 1 and then model the queue size (pay attention to the number of non elements). Pay attention to judge whether the queue is empty. If the queue is empty and still out of the queue, an error will be reported.
- Judge whether the queue is empty: return yes or no.
- Calculate the number of elements in the queue: returns the number of elements in the queue.
- tips 1: why should the queue size be modeled after team leader and team tail + 1—— If the pointer points to the end of the queue, the operation can re point it to the head of the queue, so as to realize the circular linked list.
- tips 2: how to determine whether the queue is full—— (1) Special judgment of flag bit is added, (2) the queue is full when the queue tail pointer is in front of the queue head pointer (if it coincides with the queue head pointer, it is impossible to judge whether the queue is empty or full)
- tips 3: how to return the number of elements in a pair of columns—— It can be divided into two cases. If the end of the queue is less than the head of the queue, the end of the queue pointer + queue size - head of the queue pointer can be returned.
Picture demonstration of joining and leaving the team
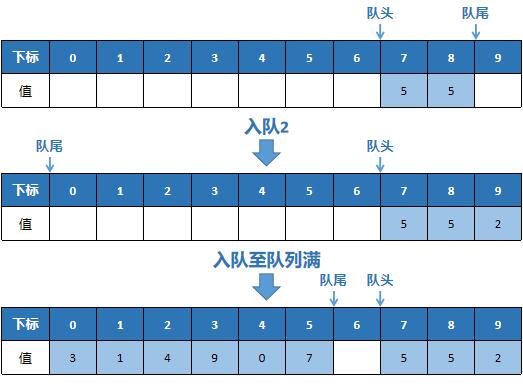
Code example
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
//Custom queue structure
typedef struct my_queue
{
int front, tail;
int size;
int* data;
}my_queue;
//Initialize queue
my_queue* init_queue(int num)
{
my_queue* t = (my_queue*)malloc(sizeof(my_queue));
t -> front = 0;
t -> tail = 0;
t -> size = num;
t -> data = (int*)malloc(sizeof(int) * num);
return t;
}
//Queue operation
//Return value: 1 succeeded, 0 failed
int queue_push(my_queue* que, int num)
{
if((que -> tail + 1) % que -> size == que -> front) return 0;
que -> data[que -> tail] = num;
que -> tail = (que -> tail + 1) % que -> size;
return 1;
}
//Out of line operation
int queue_pop(my_queue* que)
{
int res = que -> data[que -> front];
que -> front = (que -> front + 1) % que -> size;
return res;
}
//Judge that the queue is empty
//Return value: 1 true, 0 false
int queue_is_empty(my_queue* que)
{
if(que -> front == que -> tail) return 1;
return 0;
}
//Count the number of elements in the queue
int queue_size(my_queue* que)
{
if(que -> tail < que -> front)
return que -> tail + que -> size - que -> front;
return que -> tail - que -> front;
}
int main()
{
my_queue* que = init_queue(2);
//Queue operation test
srand(time(0));
int n;
printf("Please enter the number of tests:\n");
scanf("%d", &n);
for(int i = 0; i < n; i++)
{
int op = rand() % 3;
switch(op)
{
//Join the team
case 0:
{
if(queue_push(que, i))
printf("element %d Team success!\n", i);
else printf("Failed to join the team!\n");
break;
}
//Out of the team
case 1:
{
if(queue_is_empty(que)) break;
printf("The outgoing element is%d\n", queue_pop(que));
break;
}
//Number of read elements
case 2:
{
printf("The number of elements in the queue is:%d\n", queue_size(que));
break;
}
}
}
return 0;
}
Monotone queue
Basic concepts
- We have a queue in which the elements in the stack are either (non strict) monotonically increasing or (non strict) monotonically decreasing. Then this queue is a monotonic queue
- (no, it's still so plain and boring. Can you believe it)
Graphic maintenance monotone queue
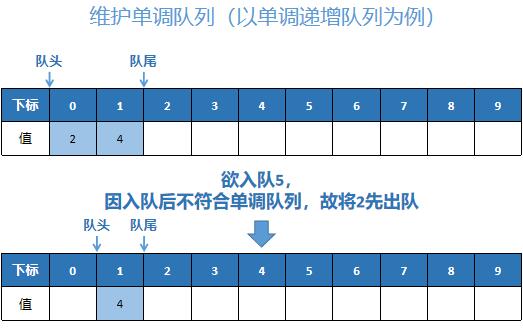
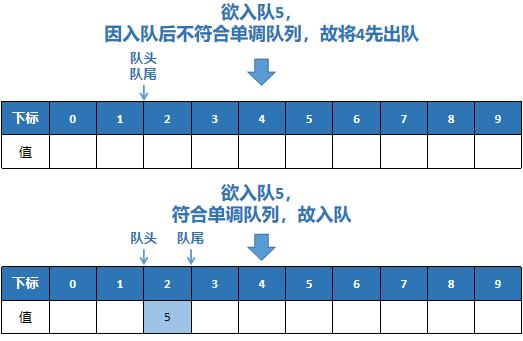
Related topics
The questions using monotonous queue encountered in this konjaku are very small QAQ. Take out the previous ones and continue to update the relevant questions if you encounter monotonous queue later!