2.3 chain representation and implementation of linear table

(Note: all codes have been successfully tested. Compilation environment: devC + +)

(1) Review: (advantages and disadvantages of linear sequential storage structure)

advantage:

1. There is no need to add additional storage space to represent the logical relationship between elements in the table.

2. You can quickly access elements anywhere in the table.

Disadvantages:

1. Insert and delete operations require moving a large number of elements. (time consuming)

2. When the length of the linear table changes greatly, it is difficult to determine the capacity of the storage space.

3. Causing "fragmentation" of storage space.

(2) Linked storage structure of linear list (linked list)

1. Single linked list

Textbook concept: use a set of storage units with arbitrary addresses to store the data elements in the linear table.

Element (image of data element) + pointer (indicating the storage location of subsequent elements) = node (representing data element or image of data element)

A linear list represented by "sequence of nodes" is called a linked list.

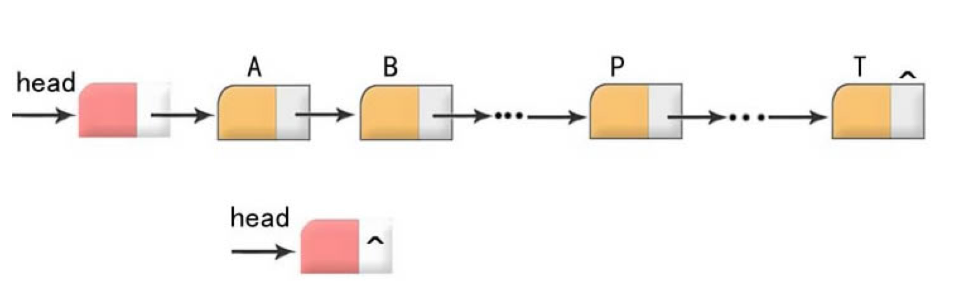
Taking the storage address of the first data element in the linear table as the address of the linear table is called the head pointer of the linear table.

Sometimes, for the convenience of operation, a "head node" is added before the first node, and the pointer to the head node is the head pointer of the linked list.

When the linear table is null, the pointer field of the header node is null.

Understanding (key points):

• Linked list is a common data structure. It connects some column data nodes into a data chain through pointers. Compared with arrays, linked lists have better dynamics (non sequential storage).

• The data field is used to store data, and the pointer field is used to establish the connection with the next node.

• When establishing a linked list, you do not need to know the total amount of data in advance, you can randomly allocate space (the memory of the linked list is discontinuous), and you can efficiently insert or delete data at any position in the linked list in real time (you only need to modify the pointer).

• The overhead of the linked list is mainly the access order and the space loss of the organization chain (the overhead of pointer domain space).

Simply understand the difference between array and linked list:

Array: allocate a contiguous storage area at one time.

• Advantages: high efficiency of random access to elements.
• Disadvantages: 1. A continuous storage area needs to be allocated (a large area may fail to allocate).

2. It is inefficient to delete and insert an element.

Linked list: there is no need to allocate a continuous storage area at one time, only n node storage areas need to be allocated, and the relationship is established through the pointer.

• Advantages: 1. No need for a continuous storage area.

  2. Deleting and inserting an element is efficient.

• Disadvantages: random access to elements is inefficient.

1.1 code description of node and single linked list

Node definition:

The node type of the linked list is actually a structure variable, which contains a data field and a pointer field:

• The data field is used to store data;

• The pointer field is used to establish the connection with the next node. When this node is the tail node, the value of the pointer field is NULL;

/* C Single linked list storage structure of language linear table */
typedef struct  LNode {
      ElemType      data;  // Data field typedef int ElemType;
      struct LNode   *next;  // Pointer field
   } LNode;

typedef struct LNode *LinkList; //Defines the header pointer.

understand:

p->data/p->next/p->next->data;

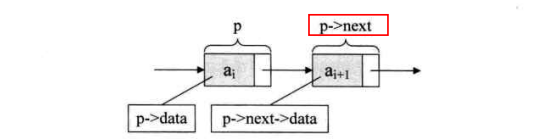
Minor editor analysis: if p is the pointer to the ith element of the linear table, the data field of node a(i) can be represented by p - > data, and its value is the data element. The pointer field of node a(i) can be represented by p - > next; p - > next points to the i + 1st element, that is, the pointer to a(i+1). Therefore, p - > next - > data is a(i+1);

Initialization of linked list:

/* Initialize linked linear list */
Status InitList(LinkList &L)   //typedef int Status;
{ 
    L=(LinkList)malloc(sizeof(LNode));    //c++: L = new LNode;
    if(!L) // Storage allocation failed 
            return ERROR;
    L->next=NULL; //Pointer field is null 

    return OK;
}

Judge whether the linked list is empty:

/* Initial condition: the linked linear table L already exists. Operation result: if L is an empty table, it returns TRUE, otherwise it returns FALSE */
Status ListEmpty(LinkList L)
{ 
    if(L->next)
            return FALSE;
    else
            return TRUE;
}

Clear the single linked list: (core idea: move the working pointer backward, clear it in turn, and free the memory)

/* Initial condition: the linked linear table L already exists. Operation result: reset L to an empty table */
Status ClearList(LinkList &L)
{ 
	LinkList p,q;
	p=L->next;           // p points to the first node 
	while(p)           
	{
		q=p->next;
		free(p);
		p=q;
	}
	L->next=NULL;        // The header node pointer field is null
	return OK;
}

Return the number of data elements in the linked list:

/* Initial condition: linked linear table l already exists. Operation result: returns the number of data elements in L */
int ListLength(LinkList L)
{
    int i=0;
    LinkList p=L->next; // p points to the first node 
    while(p)                        
    {
        i++;
        p=p->next;
    }
    return i;
}

Use e to return the value of the ith data element in L: (core idea: move the working pointer backward and traverse the search)

Algorithm idea:

(1) Declare a pointer p to the first node of the linked list, and initialize i from 1;

(2) When J < I, traverse the linked list, move the pointer of p backward and continuously point to the next node, and j accumulates 1;

(3) If p is empty at the end of the linked list, it indicates that the ith node does not exist;

(4) Otherwise, if the search is successful, the data of node p will be returned.

/* Initial condition: linked linear table l already exists, 1 ≤ i ≤ ListLength(L) */
Status GetElem(LinkList L,int i,ElemType &e)
{
	int j;
	LinkList p;		// Declare a node p 
	p = L->next;		// Let p point to the first node of the linked list L 
	j = 1;		//  j is the counter 
	while (p && j<i)  // When p is not empty or the counter j is not equal to i, the loop continues 
	{   
		p = p->next;  // Let p point to the next node 
		++j;
	}
	if ( !p || j>i ) 
		return ERROR;  //  The ith element does not exist 
	e = p->data;   //  Take the data of the i th element 
	return OK;
}

Return the bit order of the first data element in L that satisfies the relationship with e: (core idea: move the working pointer backward and traverse the linked list to determine whether it meets the conditions)

int LocateElem(LinkList L,ElemType e)
{
    int i=0;
    LinkList p=L->next;
    while(p)
    {
        i++;
        if(p->data==e) 
                return i;
        p=p->next;
    }

    return 0;
}

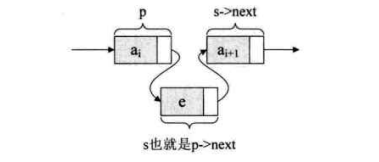
Element insertion of single linked list:

Illustration:

Algorithm idea:

(1) Declare a pointer p to the chain header node, and initialize j from 1.

(2) When J < I, traverse the linked list; let the pointer of p move backward and continuously point to the next node, and j accumulates 1.

(3) If p is empty at the end of the linked list, it indicates that the ith node does not exist.

(4) Otherwise, the search is successful and an empty node s is generated in the system.

(5) Assign the data element e to s - > data.

(6) It can be seen from the diagram that the insertion standard statement of single linked list is s - > next = P - > next; P - > next = s; (the order must not be exchanged).

(7) Return success.

Status ListInsert(LinkList &L,int i,ElemType e)
{ 
	int j;
	LinkList p,s;
	p = L;   
	j = 1;
	while (p && j < i)    
	{
		p = p->next;
		++j;
	} 
	if (!p || j > i) 
		return ERROR;  
	s = (LinkList)malloc(sizeof(LNode));  
	s->data = e;  
	s->next = p->next;      /* Assign the successor node of p to the successor node of s  */
	p->next = s;          /* Assign s to the successor of p */
	return OK;
}

Element deletion of single linked list:

Illustration:

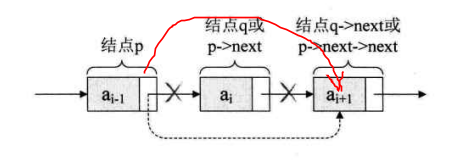
Bypass the previous node and point to the subsequent node.

Algorithm idea:

(1) Declare a node p to point to the first node in the linked list, and initialize j from 1.

(2) When J < I, traverse the linked list, make the pointer of p move backward, constantly point to the next node, and j accumulates.

(3) If p is empty at the end of the linked list, the ith element does not exist.

(4) Otherwise, the search is successful, and the node to be deleted p - > next is assigned to q.

(5) The deletion standard statement of single linked list p - > next = q - > next.

(6) Assign the data in the q node to e as a return.

(7) Release q node.

Status ListDelete(LinkList &L,int i,ElemType &e) 
{ 
	int j;
	LinkList p,q;
	p = L->next;
	j = 1;
	while (p && j < i)	
	{
        p = p->next;
        ++j;
	}
	if (!(p->next) || j > i) 
	    return ERROR;           
	q = p->next;
	p->next = q->next;			
	e = q->data;              
	free(q);                   
	return OK;
}

Reversal of single linked list: (header node)

void ReverseList(LinkList &L)
{
    LinkList old_head, new_head, Temp;
    new_head = NULL;
    old_head = L->next;

    while ( old_head )  {
        Temp = old_head->next;
        old_head->next = new_head;
        new_head = old_head;  
        old_head = Temp; 
    }
    
	L->next = new_head;
}

(static linked list, circular linked list and two-way linked list will be released in succession)

I hope it can be helpful to you. If you find any errors, please give feedback in time.